
3.已知空间三点A(1,1,1)、B(-1,0,4)、C(2,-2,3),则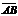 与
与 的夹角θ的大小是_________.
的夹角θ的大小是_________.
2.在正方体A-C1中,E、F分别为D1C1与AB的中点,则A1B1与截面A1ECF所成的角为 ( )
A.arctan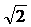 B.arccos
B.arccos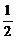 C.arcsin
C.arcsin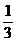 D.都不对
D.都不对
[填空题]
1.设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若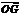 =x
=x +y
+y +z
+z ,则(x,y,z)为
( )
,则(x,y,z)为
( )
A (
(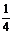 ,
, ,
, ) B
) B (
( ,
,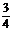 ,
,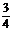 )
)
C (
(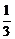 ,
,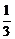 ,
,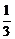 ) D
) D (
(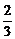 ,
,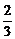 ,
,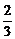 )
)
2.求点面距离,线面距离、面面距离及异面直线的距离的方法:
同步练习 9.8用空间向量求角和距离
[选择题]
1.求线线角、线面角、二面角的方法:
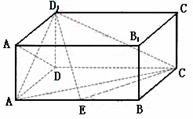 [例1] (2005江西)如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;
[例1] (2005江西)如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为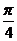 .
.
解:以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
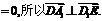
(2)因为E为AB的中点,则E(1,1,0),
从而 ,
,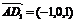 ,
,
设平面ACD1的法向量为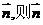 不与y轴垂直,可设
不与y轴垂直,可设
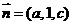 ,则
,则
也即 ,得
,得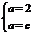 ,从而
,从而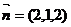 ,
,
∴点E到平面AD1C的距离:
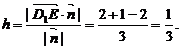
(3)
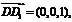
设平面D1EC的法向量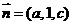 ,
,
由

依题意
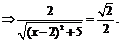
∴ (不合,舍去),
(不合,舍去),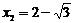 .
.
∴AE= 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为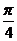
[例2](2005全国)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,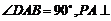 底面ABCD,
底面ABCD,
 且PA=AD=DC=
且PA=AD=DC=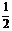 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
(Ⅰ)证明:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,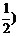
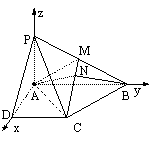

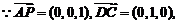

又由题设知AD⊥DC,且AP与与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD
(Ⅱ)解:因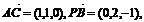
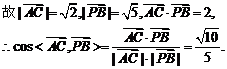
由此得AC与PB所成的角为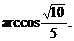
(Ⅲ)解:设平面ACM的法向量为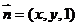 ,
,
由 得:
得: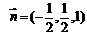
设平面BCM的法向量为 同上得
同上得
 ∴
∴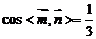
结合图形可得二面角A-MC-B为
解法2:在MC上取一点N(x,y,z),则存在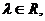 使
使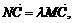
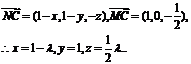
要使

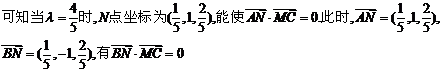

为所求二面角的平面角.
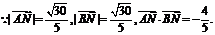

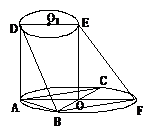
[例3]如图,AF DE分别是⊙O
DE分别是⊙O ⊙O1的直径
⊙O1的直径 AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE//AD
AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE//AD
(Ⅰ)求直线BD与EF所成的角;
(Ⅱ)求异面直线BD和EF之间的距离.
解:(Ⅰ)以O为原点,BC AF
AF OE所在直线为坐标轴,建立空间直角坐标系(如图所示),
OE所在直线为坐标轴,建立空间直角坐标系(如图所示),
则O(0,0,0),A(0,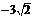 ,0),B(
,0),B(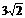 ,0,0),D(0,
,0,0),D(0,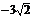 ,8),E(0,0,8),F(0,
,8),E(0,0,8),F(0, ,0)
,0)
所以,


设异面直线BD与EF所成角为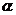 ,则
,则
直线BD与EF所成的角为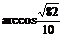
(Ⅱ)设向量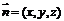 与BD、EF都垂直,则有
与BD、EF都垂直,则有
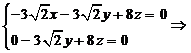
 ,
,
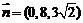 ∴ BD、EF之间的距离
∴ BD、EF之间的距离
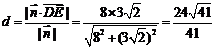
4.(2,1, ),dAB=
),dAB=

4. 已知A(3,2,1)、B(1,0,4),则线段AB的中点坐标和长度分别是 , .
◆答案提示: 1. C; 2. A; 3. 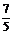 ;
;
3.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k= ___
2. 直三棱柱A1B1C1-ABC,∠BCA=90°,D1、F1分别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是 ( )
A.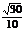 B.
B.  C.
C.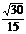 D.
D.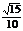
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com