
1.物理过程的分析。
3.利用动能定律求变力的功。
2.灵活运用动能定理处理多过程问题。
1.复习掌握动能定理的内容。
9.在60°的二面角的棱上,有A、B两点,线段AC、BD分别在二面角的两个面内,且都垂直于AB,已知AB=4,AC=6,BD=8.
 ⑴求CD的长度; ⑵求CD与平面
⑴求CD的长度; ⑵求CD与平面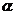 所成的角
所成的角
解:⑴因为
 ,故有
,故有
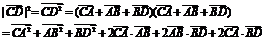 ,
,
∵CA⊥AB,BD⊥AB,∴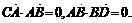
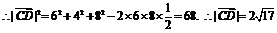 .
.
(2)过C作CE⊥平面α于E,连接AE、CE在△ACE中,CE=6sin60°=3 ,连接DE,则∠CDE就是CD与平面α所成角。
,连接DE,则∠CDE就是CD与平面α所成角。
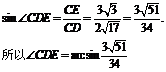
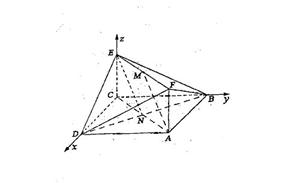
8. 如图,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点
如图,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点
求:(1)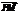 与
与 所成的角;
所成的角;
(2)P点到平面EFB的距离;
(3)异面直线PM与FQ的距离
解:建立空间直角坐标系,
则D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),
则由中点坐标公式得P(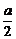 ,0,
,0,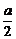 )、Q(
)、Q(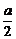 ,
,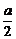 ,0)
,0)
(1)∴ =(-
=(-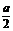 ,0,
,0,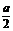 ),
), =(
=(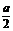 ,-
,-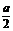 ,-a),
,-a),
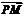 ·
·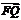 =(-
=(-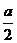 )×
)×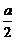 +0+
+0+ ×(-a)=-
×(-a)=-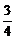 a2,
a2,
且|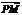 |=
|= 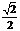 a,|
a,| |=
|= 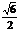 a.
a.
∴cos〈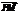 ,
,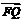 〉=
〉=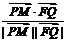 =
= =-
=-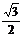 .
.
故得两向量所成的角为150°
(2)设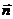 =(x,y,z)是平面EFB的法向量,
=(x,y,z)是平面EFB的法向量,
即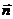 ⊥平面EFB,∴
⊥平面EFB,∴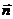 ⊥
⊥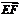 ,
,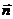 ⊥
⊥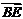 .
.
又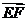 =(-a,a,0),
=(-a,a,0),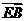 =(0,a,-a),
=(0,a,-a),
即有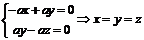 ,
,
取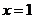 ,则
,则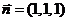 .
.
∵ 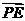 =(
=(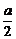 ,0,
,0,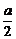 ).
).
∴ 设所求距离为d,则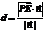 =
=  a.
a.
(3)设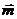 =(x1,y1,1)是两异面直线的公垂线的方向向量,
=(x1,y1,1)是两异面直线的公垂线的方向向量,
则由 =(-
=(-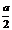 ,0,
,0,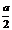 ),
),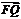 =(
=(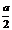 ,-
,-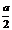 ,-a),
,-a),
得 ,
,
而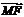 =(0,a,0)
=(0,a,0) 所求距离
所求距离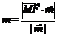 =
=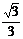 a.
a.
7.(2004全国·河北)如下图,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
(1)求点P到平面ABCD的距离;
(2)求面APB与面CPB所成二面角的大小.

解(1):如下图,作PO⊥平面ABCD,垂足为点O.连结OB、OA、OD,OB与AD交于点E,连结PE.
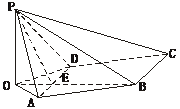
∵AD⊥PB,∴AD⊥OB.
∵PA=PD,∴OA=OD.
于是OB平分AD,点E为AD的中点,∴PE⊥AD.由此知∠PEB为面PAD与面ABCD所成二面角的平面角,∴∠PEB=120°,∠PEO=60°.由已知可求得PE=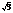 ,
,
∴PO=PE·sin60°=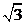 ×
× =
=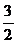 ,即点P到平面ABCD的距离为
,即点P到平面ABCD的距离为 .
.
(2)解法一:如下图建立直角坐标系,其中O为坐标原点,x轴平行于DA.
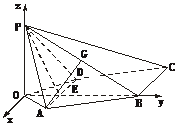
P(0,0, ),B(0,
),B(0, ,0),PB中点G的坐标为(0,
,0),PB中点G的坐标为(0,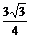 ,
, ),连结AG.
),连结AG.
又知A(1,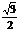 ,0),C(-2,
,0),C(-2,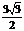 ,0).
,0).
由此得到 =(1,-
=(1,-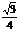 ,-
,-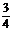 ),
),
 =(0,
=(0,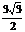 ,-
,-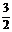 ),
), =(-2,0,0).
=(-2,0,0).
于是有 ·
· =0,
=0,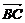 ·
· =0,
=0,
∴ ⊥
⊥ ,
,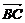 ⊥
⊥ .
.  ,
,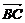 的夹角θ等于所求二面角的平面角.
的夹角θ等于所求二面角的平面角.
于是cosθ=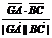 =-
=- ,
,
∴所求二面角的大小为π-arccos .
.
解法二:如下图,取PB的中点G,PC的中点F,连结EG、AG、GF,
则AG⊥PB,FG∥BC,FG=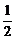 BC.
BC.

∵AD⊥PB,∴BC⊥PB,FG⊥PB.∴∠AGF是所求二面角的平面角.
∵AD⊥面POB,∴AD⊥EG.
又∵PE=BE,∴EG⊥PB,且∠PEG=60°.
在Rt△PEG中,EG=PE·cos60°=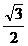 ,
,
在Rt△GAE中,AE=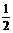 AD=1,于是tan∠GAE=
AD=1,于是tan∠GAE= =
= 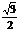 .
.
又∠AGF=π-∠GAE,
∴所求二面角的大小为π-arctan .
.
6.(2004浙江文)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=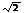 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求证AM⊥平面BDF;
(Ⅲ)求二面角A-DF-B的大小;

解:(Ⅰ)建立如图所示的空间直角坐标系.
设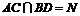 ,连接NE,
,连接NE,
则点N、E的坐标分别是( 、(0,0,1),
、(0,0,1),
∴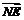 =(
=(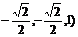 ,
,
又点A、M的坐标分别是 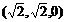 、(
、( .
.
∴ 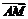 =(
=(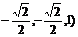
∴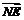 =
=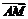 且
且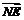 与AM不共线,∴NE∥AM.
与AM不共线,∴NE∥AM.
又∵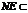 平面BDE,
平面BDE, 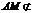 平面BDE,
平面BDE,
∴AM∥平面BDF.
(Ⅱ)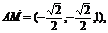
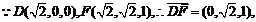

(Ⅲ)∵AF⊥AB,AB⊥AD,AF∩AD=A,
∴AB⊥平面ADF.
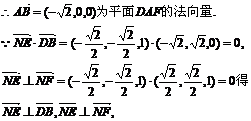
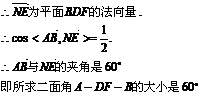
5. 设A(2,3,1),B(4,1,2),C(6,3,7),D(-5,-4,8),求D到平面ABC的距离.
解:∵A(2,3,1),B(4,1,2),C(6,3,7),D(-5,-4,8),
∴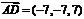 ;
;
设平面ABC的法向量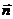 =(x,y,z),则
=(x,y,z),则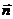 ·
· =0,
=0,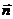 ·
·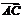 =0,
=0,
∴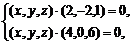
即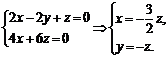
令z=-2,则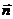 =(3,2,-2)
=(3,2,-2) 由点到平面的距离公式:
由点到平面的距离公式:
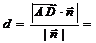
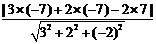 =
=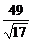 =
= .
.
∴点D到平面ABC的距离为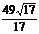 .
.
4.二面角α-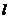 -β的平面角为120°,A、B∈
-β的平面角为120°,A、B∈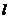 ,AC
,AC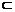 α,BD
α,BD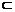 β,AC⊥
β,AC⊥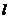 ,BD⊥
,BD⊥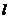 ,若AB=AC=BD=
,若AB=AC=BD=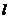 ,则CD的长为 .
,则CD的长为 .
◆答案提示:1.A; 2. A; 3.120°; 4. 2
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com