
2、16世纪葡萄牙著名诗人德·卡蒙斯这样深情地描绘他的祖国:“大陆,在这里是尽头; 大海,在这里才开头。”诗句中反映了他对祖国引以为豪的是
A.成为“海上马车夫” B.垄断欧亚之间的贸易
C.率先开辟新航路 D.处于欧洲商业中心地位
1、最早开辟新航路的迪亚士曾经说过,他航行的目的是“为上帝和皇帝陛下服务,给处于黑暗中的人们带去光明,并像所有人渴望的那样去发财致富”。其中“给处于黑暗中的人们带去光明”是指
A. 给土著人带去人文主义思想 B. 给渴望发财的人带去黄金
C. 给土著人带去皇帝的恩典 D. 使土著人皈依天主教
(五)课外练习:
 (1)对放在水平面上的质量为M的物体,施与水平拉力F,使它从静止开始运动时间t后撤去外力F,又经时间t停下来,则:
(1)对放在水平面上的质量为M的物体,施与水平拉力F,使它从静止开始运动时间t后撤去外力F,又经时间t停下来,则:
A.撤去力F的时刻,物体的动量最大;
B.物体受到的阻力大小等于F;
C.物体克服阻力做的功为F2 t2/4M
D.F对物体做功的平均功率为F2 t/4M。
 (2)
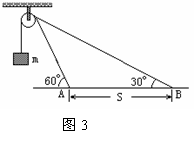
如图3所示,人拉着绳的一端由A走到B,使质量为m的物体匀速上升,已知A、B两点的水平距离为S,求人对物体做的功?
(2)
如图3所示,人拉着绳的一端由A走到B,使质量为m的物体匀速上升,已知A、B两点的水平距离为S,求人对物体做的功?
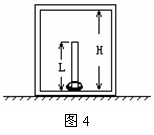
(3) 如图4所示,,箱高为H,箱中有一竖直的固定杆,
杆长为L(L<H=,它们的总质量为M。另有一个质量为m
的小球穿在杆上,球与杆间有不变的摩擦力,当小球以初速
度V0 从底部向上滑动时,恰好到达箱顶。那么在小球沿杆上升的过程中,箱对水平地面的压力为多大?
(四)课堂小结:
(1)应用动能定理求变力的功:如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能增量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
(2)应用动能定理简解多过程问题:物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程利用动能定理列式则使问题简化。
(三)巩固练习:
从离地面H高处落下一只小球,小球在运动过程中所受的空气阻力是它重力的k(k<1)倍,而小球与地面相碰后,能以相同大小的速率反弹,求:
(1)小球第一次与地面碰撞后,能够反弹起的最大高度是多少?
(2)小球从释放开始,直至停止弹跳为止,所通过的总路程是多少?
思路点拨:先据题意作出过程示意图,分析受力及运动情况,然后据动能定理列方程即可。
略解:(1)设 小球第一次与地面碰撞后,能够反弹起的最大高度是h,则由动能定理得:mg(H-h)-kmg(H+h)=0
(2)设球从释放开始,直至停止弹跳为止,所通过的总路程是S,对全过程由动能定理得mgH-kmgL=0
归纳小结:物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程利用动能定理列式则使问题简化。
(二)进行新课:
1.应用动能定理求变力的功。
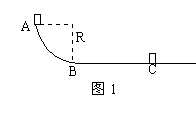 例题1、如图1所示,AB为1/4圆弧轨道,半径为R=0.8m,BC是水平轨道,长S=3m,BC处的摩擦系数为μ=1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。
例题1、如图1所示,AB为1/4圆弧轨道,半径为R=0.8m,BC是水平轨道,长S=3m,BC处的摩擦系数为μ=1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。
(先让学生自己做一做,然后老师再给予点拔)
解析:物体在从A滑到C的过程中,有重力、
AB段的阻力、BC段的摩擦力共三个力做功,WG=mgR,fBC=umg,由于物体在AB段受的阻力是变力,做的功不能直接求。根据动能定理可知:W外=0,
所以mgR-umgS-WAB=0
即WAB=mgR-umgS=1×10×0.8-1×10×3/15=6(J)
 归纳小结:如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能增量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
归纳小结:如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能增量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
2.应用动能定理简解多过程问题。
例2:如图2所示,斜面足够长,其倾角为α,
质量为m的滑块,距挡板P为S0,以初速度V0沿斜
面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失,
求:(1)滑块将向上作什么样的运动?
(2)求滑块第一次到最高点时经过的路程?
(3)求滑块在斜面上经过的总路程为多少?
解析:(1)滑块在滑动过程中,要克服摩擦力做功,其机械能不断减少;又因为滑块所受摩擦力小于滑块沿斜面方向的重力分力,所以最终会停在斜面底端。
(2)在整个过程中,受重力、摩擦力和斜面支持力作用,其中支持力不做功。设其经过的总路程为L,对全过程,由动能定理得: 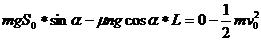
得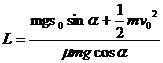
(3)滑块在斜面上经过的总路程与(2)中所求相同。
思考:
1.若物体初速度方向沿斜面向下,此题应如何解答?()
2.若物体初速度方向向上,滑块所受摩擦力大于滑块沿斜面方向的重力分力,物体运动情况如何变化?
3.若未给定初速度方向,但给定滑块所受摩擦力大于滑块沿斜面方向的重力分力,本题应如何去分析?
强调:答题一定要仔细审题,题中条件变了,物理情景会发生本质变化,对此审题定要慎重!
(一)复习提问,引入新课:
乒乓球在与地面反复的碰撞过程中,所通过的总路程如何计算最方便呢?这个问题虽然用牛顿定律结合运动学公式可以解决,但过程较复杂。
我们在踢足球时,如何求解踢球过程中,我们的脚对足球所做的功呢?人的脚在与足球接触中这个力是变化的,我们无法直接用公式W=Fscosα来计算对足球所做的功。如果能知道力对足球所做的功跟足球动能变化的关系,就能很方便地解决这个问题了。
那么,外力对物体做的功跟物体动能的变化有什么关系呢?动能定理就给出了它们之间定量的关系。
提问1:动能定理的基本内容是什么?
(学生回答:外力对物体所做的总功,等于物体动能的变化)
提问2:动能定理的表达式是怎样的?是标量式还是矢量式?
(学生回答:W合=EK2-EK1,是标量式)
提问3:如何理解动能定理?动能定理的解题步骤是怎样的?
(要求学生把上一节课的内容复习一遍)
动能定理可以由牛顿定律推导出来,原则上讲用动能定律能解决物理问题都可以利用牛顿定律解决,但在处理动力学问题中,若用牛顿第二定律和运动学公式来解,则要分阶段考虑,且必须分别求每个阶段中的加速度和末速度,计算较繁琐。但是,我们用动能定理来解就比较简捷。本节课就研究动能定理解决某些动力学问题的优越性。
多媒体设备
练习、讨论、讲授
2.物体受力情况分析及各力做功情况分析。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com