
20.(本小题8分)
设等差数列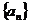 的前n项和为
的前n项和为 ,已知
,已知 =12,且
=12,且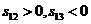 。
。
(1)求公差d的范围;
(2)前几项和最大?并说明理由。
19.(本小题8分)
△ABC中,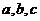 分别是A,B,C所对的边,S是该三角形的面积,且
分别是A,B,C所对的边,S是该三角形的面积,且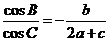
(1)求∠B的大小;
(2)若 =4,
=4,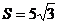 ,求
,求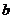 的值。
的值。
18.(本小题8分)
数列{ a n }的前项和为S n = 4n 2 – n + 2,求该数列的通项公式.
17.将正⊿ABC分割成
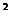 (
( ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,则f(3)= .
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,则f(3)= .
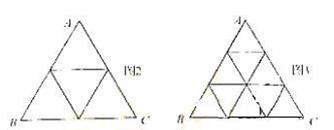
16.数列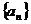 中,
中,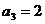 ,
,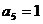 ,数列
,数列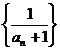 是等差数列,则
是等差数列,则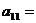
15. 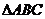 中,若b=2a , B=A+60°,则A=
.
中,若b=2a , B=A+60°,则A=
.
14.△ABC中,已知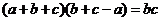 ,则A的度数等于
,则A的度数等于
13.《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给五人,使每人成等差数列,且使最大的三份之和的 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是
12. 在等差数列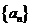 中,
中,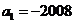 ,其前
,其前 项的和为
项的和为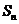 .若
.若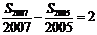 ,则
,则 (
)
(
)
A.-2007 B.-2008 C.2007 D.2008
11.数列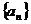 中,若
中,若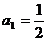 ,
,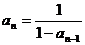 (
(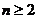 ,
,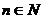 ),则
),则 的值为( )
的值为( )
A.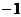 B.
B.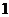 C.
C. D.
D.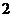
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com