
3.(2010年新课标全国卷)柳宗元在《封建论》中评价秦始皇废封建、行郡县说:“其为制,公之大者也┅┅公天下之端自始皇。”郡县制为“公天下”之开端,主要体现在
A.百姓不再是封君的属民 B.更有利于皇帝集权
C.制度法令的统一 D.依据才干政绩任免官吏
[解析]D 此题考查学生解读文字信息的能力,以材料提供的新角度解读秦始皇时期的郡县制,也体现研究性学习的考查。材料主要意思为唐朝的柳宗元肯定郡县制“公天下”,郡县制官吏由皇帝任免,比分封制下分封贵族爵位更利于国家政局的安定。故选A。
2.(2010年广东卷)在中国古代“家国一体”的社会中,忠孝观念源远流长,其源头是
A. 宗法制 B. 郡县制 C.君主专制 D. 中央集权制
[解析]A 宗法制把家、国联系在一起,为人臣者忠于君主,为人子者孝顺长辈,忠孝观念根源于以嫡长子继承制为中心的父系宗法制度。 (评:这道题可能有学生考虑到“忠君”,会选择“君主专制”,本题的干扰项有点难度。再看源头,忠君之源,依然是宗法制。)
说明:本资料精选全国各地高考真题和全国新课标地区名校月考、联考、大市模拟试题,对备战2011年高考具有较好的指导作用。
1.(2010年广东卷)唐代和宋代都有谏官。唐代谏官由宰相荐举,主要评议皇帝得失;宋代谏官由皇帝选拔,主要评议宰相是非。这说明
A.唐代君主的权力不受制约 B.唐代以谏官削弱宰相的权力
C.宋代谏官向宰相和皇帝负责 D.宋代君主专制的程度高于唐代
[解析]D 唐代谏官主要评议皇帝得失到宋代主要评议宰相是非。这反映了君主专制的加强,即从某个侧面说明了宋代君主专制的程度高于唐代。A君权“不受制约”提法错误;宋代以谏官削弱宰相的权力,B排除;宋代谏官由皇帝选拔,向皇帝负责,C项也不对。
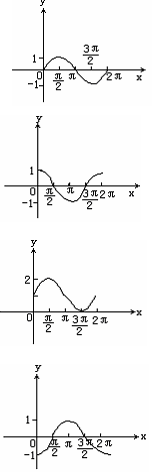
例1 作下列函数的简图
(1)y=sinx,x∈[0,2π], (2)y=cosx,x∈[0,2π],
(3)y=1+sinx,x∈[0,2π], (4)y=-cosx,x∈[0,2π],
 解:(1)列表
解:(1)列表
|
X |
0 |
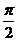 |
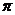 |
 |
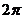 |
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
(2)列表
|
X |
0 |
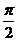 |
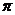 |
 |
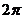 |
|
Cosx |
1 |
0 |
-1 |
0 |
1 |
(3)列表
|
X |
0 |
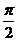 |
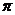 |
 |
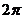 |
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
|
1+sinx |
1 |
2 |
1 |
0 |
1 |
(4)列表
|
X |
0 |
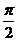 |
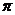 |
 |
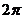 |
|
Cosx |
1 |
0 |
-1 |
0 |
1 |
|
-cosx |
-1 |
0 |
1 |
0 |
-1 |
例2 利用正弦函数和余弦函数的图象,求满足下列条件的x的集合:
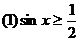
解:作出正弦函数y=sinx,x∈[0,2π]的图象:
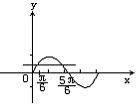
由图形可以得到,满足条件的x的集合为:

解:作出余弦函数y=cos,x∈[0,2π]的图象:
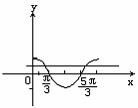
由图形可以得到,满足条件的x的集合为:
4.用正弦函数和余弦函数的图象解最简单的三角不等式:通过例2介绍方法
3.用五点法作正弦函数和余弦函数的简图(描点法):
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:
(0,0) (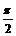 ,1) (p,0) (
,1) (p,0) (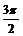 ,-1) (2p,0)
,-1) (2p,0)
只要这五个点描出后,图象的形状就基本确定了.因此在精确度不太高时,常采用五点法作正弦函数和余弦函数的简图,要求熟练掌握.
探究:
(1)y=cosx,
xÎR与函数y=sin(x+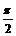 ) xÎR的图象相同
) xÎR的图象相同
(2)将y=sinx的图象向左平移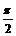 即得y=cosx的图象
即得y=cosx的图象
 (3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是
(3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是
(0,1) (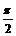 ,0) (p,-1) (
,0) (p,-1) (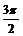 ,0) (2p,1)
,0) (2p,1)
2.用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象(几何法):为了作三角函数的图象,三角函数的自变量要用弧度制来度量,使自变量与函数值都为实数.在一般情况下,两个坐标轴上所取的单位长度应该相同,否则所作曲线的形状各不相同,从而影响初学者对曲线形状的正确认识.

第一步:列表 首先在单位圆中画出正弦线和余弦线.在直角坐标系的x轴上任取一点
首先在单位圆中画出正弦线和余弦线.在直角坐标系的x轴上任取一点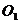 ,以
,以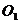 为圆心作单位圆,从这个圆与x轴的交点A起把圆分成几等份,过圆上的各分点作x轴的垂线,可以得到对应于角
为圆心作单位圆,从这个圆与x轴的交点A起把圆分成几等份,过圆上的各分点作x轴的垂线,可以得到对应于角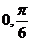 ,
,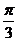 ,
,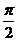 ,…,2π的正弦线及余弦线(这等价于描点法中的列表).
,…,2π的正弦线及余弦线(这等价于描点法中的列表).
第二步:描点.我们把x轴上从0到2π这一段分成几等份,把角x的正弦线向右平行移动,使得正弦线的起点与x轴上相应的点x重合,则正弦线的终点就是正弦函数图象上的点.
第三步:连线 用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数y=sinx,x∈[0,2π]的图象.
用光滑曲线把这些正弦线的终点连结起来,就得到正弦函数y=sinx,x∈[0,2π]的图象.
现在来作余弦函数y=cosx,x∈[0,2π]的图象:
第一步:列表 表就是单位圆中的余弦线.
表就是单位圆中的余弦线.
第二步:描点.把坐标轴向下平移,过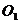 作与x轴的正半轴成
作与x轴的正半轴成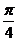 角的直线,
角的直线,
又过余弦线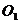 A的终点A作x轴的垂线,它与前面所作的直线交于A′,那么
A的终点A作x轴的垂线,它与前面所作的直线交于A′,那么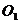 A与AA′长度相等且方向同时为正,我们就把余弦线
A与AA′长度相等且方向同时为正,我们就把余弦线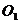 A“竖立”起来成为AA′,用同样的方法,将其它的余弦线也都“竖立”起来.再将它们平移,使起点与x轴上相应的点x重合,则终点就是余弦函数图象上的点.
A“竖立”起来成为AA′,用同样的方法,将其它的余弦线也都“竖立”起来.再将它们平移,使起点与x轴上相应的点x重合,则终点就是余弦函数图象上的点.
第三步:连线.用光滑曲线把这些竖立起来的线段的终点连结起来,就得到余弦函数y=cosx,x∈[0,2π]的图象.
以上我们作出了y=sinx,x∈[0,2π]和y=cosx,x∈[0,2π]的图象,现在把上述图象沿着x轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx,x∈R和y=cosx,x∈R的图象,分别叫做正弦曲线和余弦曲线.


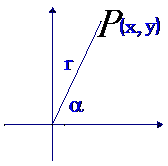
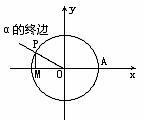
1. 正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M,则有
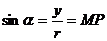 ,
,
向线段MP叫做角α的正弦线,有向线段OM叫做角α的余弦线.
1 设
设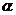 是一个任意角,在
是一个任意角,在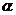 的终边上任取(异于原点的)一点P(x,y)
的终边上任取(异于原点的)一点P(x,y)
则P与原点的距离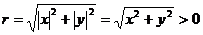
2. 比值
比值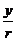 叫做
叫做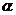 的正弦 记作:
的正弦 记作: 
比值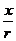 叫做
叫做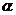 的余弦 记作:
的余弦 记作: 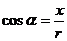
比值 叫做
叫做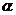 的正切 记作:
的正切 记作: 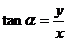
比值 叫做
叫做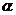 的余切 记作:
的余切 记作: 
比值 叫做
叫做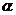 的正割 记作:
的正割 记作: 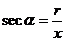
比值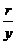 叫做
叫做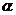 的余割 记作:
的余割 记作: 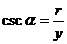
以上六种函数,统称为三角函数
今天我们要研究怎样作正弦函数、余弦函数的图象,作三角函数图象的方法一般有两种:(1)描点法;(2)几何法(利用三角函数线).但描点法的各点的纵坐标都是查三角函数表得到的数值,不易描出对应点的精确位置,因此作出的图象不够准确.几何法则比较准确.
 二、讲解新课:
二、讲解新课:
22.(本题满分14分)
设函数 ,其中
,其中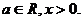
(Ⅰ)若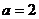 ,求曲线
,求曲线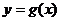 在点
在点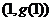 处的切线方程;
处的切线方程;
(Ⅱ)是否存在负数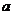 ,使
,使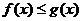 对一切正数
对一切正数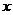 都成立?若存在,求出
都成立?若存在,求出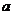 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com