21．(本小题满分13分)

设函数f(x)＝x³－x²－x+2。

(Ⅰ)求f(x)的单调区间和极值；

(Ⅱ)若当x∈[－1，2]时，－3≤af(x)+b≤3，求a－b的最大值。

()

20．(本小题满分13分)

一袋中装有大小、材质都相同的2个黑球和1个红球，甲、乙两人进行摸球游戏，规则如下：若摸中红球，则将此球放回袋中，此人继续摸球；若没有摸到红球，则将球放回袋中，由对方摸球。现由甲进行第一次摸球。

(Ⅰ)在前4次摸球中，求甲恰好摸中2次红球的概率；

(Ⅱ)设ξ为前3次摸球中，甲摸到红球的次数，求ξ的分布列和数学期望。

19．(本小题满分12分)

已知数列{a_n}的前n项和为S_n，a₁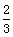＝－，满足S_n+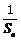+2＝a_n(n≥2)，求S_n的表达式。

18．(本小题满分12分)

为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：

(Ⅰ)估计该地区老年人中，需要志愿者提供帮助的老年人的比例；

(Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？

(Ⅲ)根据(Ⅱ)的结论，能否提出更好的调查方法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由。

附：

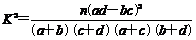
17．(本小题满分12分)

现有3名医生和6名护士。(结果用数字表示)

(Ⅰ)若将6名护士平均分成三组，共有多少种分法？

(Ⅱ)若将这9人平均分到三所学校为学生进行体检(每校1名医生和2名护士)，共有多少种分法？

16．(本小题满分12分)

已知复数z₁＝m+(4－m²)i(m∈R)，z₂＝2cosθ+(λ+3sinθ)i(m∈R)，并且z₁＝z₂，求λ的取值范围。

15．给定正整数n(n≥5)，按下述方式构成一个倒立的三角形数表(如下图)：第一行依次写上1，2，…，n，在这一行的每两个数的正中间下方分别写这两个数的和，得到下一行。依此类推，最后一行(第n行)只有一个数，记作f(n)，则f(5)＝　　；f(n)＝　　。

1　2　3　…　…　n－2　n－1　　n

3　5　…　…　…　…2n－3　 2n－1

8　…　…　…　…　…　 4n-4

　　　　　　 　…　…　…　…　…　

　　　　　　　 …　…　…　…　…　

f(n)

14．平面几何里有结论：“边长为a的正三角形内任意一点到三边的距离之和为定值”。若考察棱长为a的正四面体(即各棱长均为a的三棱锥)，则类似的结论为　　。

13．在建立两个变量y与x的回归模型中，分别选择了3个不同模型，它们的相关指数R²如下：①模型1的相关指数R²为0.98；②模型2的相关指数R²为0.50；③模型3的相关指数R²为0.23。其中拟合得最好的模型是　　。(填序号)

12．随机变量X-B(n，p)，且Eξ＝200，σξ＝10，则n＝　　。