
6.( )一定条件下,在容积不变的密闭容器中发生反应:2A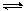 B(g)+C(s),且达到化学平衡,当升高温度时其容器内气体的密度增大,则下列判断正确的是:
B(g)+C(s),且达到化学平衡,当升高温度时其容器内气体的密度增大,则下列判断正确的是:
A、若正反应是吸热反应,则A为非气体 B、若正反应是放热反应,则A为气态
C、若在平衡体系中加入少量C,该平衡向逆反应方向移动 D、压强对该平衡的移动无影响
5. ( )对于mA(g)+nB(g)
( )对于mA(g)+nB(g) 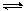 pC(g);△H达平衡后,在t1时刻,改变某一外界条件X,其速率变化曲线如图所示。下列说法正确的是:
pC(g);△H达平衡后,在t1时刻,改变某一外界条件X,其速率变化曲线如图所示。下列说法正确的是:
A、X为升高温度,且△H < 0
B、X为增大压强,且m+n>p
C、X为使用催化剂
D、X为增大A的浓度
4. ( )在一定温度下,将各1molCO和水蒸气放在密闭容器中反应:CO(g)+H2O(g)
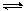 CO2(g)+H2(g),达到平衡后测得CO2为0.6mol,再通入4mol水蒸气,达到新平衡后,CO2的物质的量是: A、等于0.6mol B、等于1mol C、大于0.6mol小于1mol D、大于1mol
CO2(g)+H2(g),达到平衡后测得CO2为0.6mol,再通入4mol水蒸气,达到新平衡后,CO2的物质的量是: A、等于0.6mol B、等于1mol C、大于0.6mol小于1mol D、大于1mol
3.( )在一定温度下,将一定质量的混合气体在密闭容器中发生反应aA(g)+bB(g)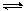 cC(g)+dD(g),达到平衡时测得B气体的浓度为0.6mol/L,恒温下将密闭容器的容积扩大1倍,重新达到平衡时,测得B气体的浓度为0.4mol/L,下列叙述中正确的是:
cC(g)+dD(g),达到平衡时测得B气体的浓度为0.6mol/L,恒温下将密闭容器的容积扩大1倍,重新达到平衡时,测得B气体的浓度为0.4mol/L,下列叙述中正确的是:
A、a+b>c+d B、平衡向右移动
C、重新达平衡时,A气体浓度增大 D、重新达平衡时,D的体积分数减小
2.( )反应NH4HS(s) 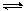 NH3(g)+H2S(g)在某温度下达到平衡,下列各种情况中,不能使平衡发生移动的是: A、其它条件不变时,通入SO2气体 B、移走一部分NH4HS固体
NH3(g)+H2S(g)在某温度下达到平衡,下列各种情况中,不能使平衡发生移动的是: A、其它条件不变时,通入SO2气体 B、移走一部分NH4HS固体
C、容器体积不变,充入氮气 D、充入氮气,保持压强不变
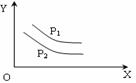
1. ( )反应:L(s)+aG(g) 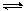 bR(g)达到平衡时,温度和压强对该反应的影响如上图所示。图中:压强p1>p2,X轴表示温度,Y轴表示平衡混合气中G的体积分数。据此可判断:
bR(g)达到平衡时,温度和压强对该反应的影响如上图所示。图中:压强p1>p2,X轴表示温度,Y轴表示平衡混合气中G的体积分数。据此可判断:
A、上述反应是放热反应 B、上述反应是吸热反应 C、a>b D、a<b
2. 外因对平衡移动的影响
(1)浓度: 增大反应物浓度或减少生成物浓度, 平衡 移动;
减少反应物浓度或增大生成物浓度, 平衡 移动。
(2)温度: 升温,平衡向 方向移动;
降温,平衡向 方向移动。
(3)压强: 对于有气体参加的可逆反应,加压,平衡向气体体积 方向移动;
减压,平衡向气体体积 方向移动。
(4)催化剂: 对化学平衡 ,但能缩短到达平衡所需的时间.
[总结]勒夏持列原理:
 [例1]以2A(g) +B(g) 2C(g) △H<0为例,画出平衡条件改变时的υ- t 图 ,并思考在下列条件下A的转化率、C%和混合气体的平均摩尔质量如何变化?
[例1]以2A(g) +B(g) 2C(g) △H<0为例,画出平衡条件改变时的υ- t 图 ,并思考在下列条件下A的转化率、C%和混合气体的平均摩尔质量如何变化?
① 增大c(A) ③降温
② 增大P ④使用催化剂
[例2]( )已知反应A2(g)+2B2(g)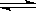 2AB2(g)的△H<0,下列说法正确的是
2AB2(g)的△H<0,下列说法正确的是
 A. 升高温度,正向反应速率增加,逆向反应速率减小
A. 升高温度,正向反应速率增加,逆向反应速率减小
B. 升高温度有利于反应速率增加,从而缩短达到平衡的时间
C. 达到平衡后,升高温度或增大压强都有利于该反应平衡正向移动
D. 达到平衡后,降低温度或减小压强都有利于该反应平衡正向移动
[巩固练习]
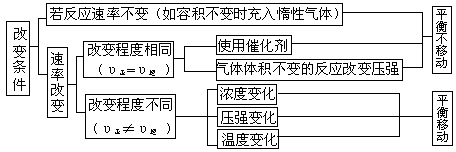
1.定义:平衡移动就是一个“平衡状态→不平衡状态→新的平衡状态”的过程。一定条件下的平衡体系,条件改变后,可能发生平衡移动。可总结如下:
15.(2008·北京崇文)已知函数f(x)=ax2+ax和g(x)=x-a,其中a∈R且a≠0.
(1)若函数f(x)与g(x)的图象的一个公共点恰好在x轴上,求a的值;
(2)若函数f(x)与g(x)图象相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的a值;如果没有,请说明理由.
(3)若p和q是方程f(x)-g(x)=0的两根,且满足0<p<q<,证明:当x∈(0,p)时,g(x)<f(x)<p-a.
解:(1)设函数g(x)图象与x轴的交点坐标为(a,0),
又∵点(a,0)也在函数f(x)的图象上,
∴a3+a2=0.
而a≠0,∴a=-1.
(2)依题意,f(x)=g(x),
即ax2+ax=x-a,
整理,得ax2+(a-1)x+a=0,①
∵a≠0,函数f(x)与g(x)图象相交于不同的两点A、B,∴Δ>0,
即Δ=(a-1)2-4a2=-3a2-2a+1
=(3a-1)(-a-1)>0.
∴-1<a<且a≠0.
设A(x1,y1),B(x2,y2),且x1<x2,
由①得,x1·x2=1>0,x1+x2=-.
设点O到直线g(x)=x-a的距离为d,则d=,
|AB|=
=|x1-x2|.
∴S△OAB=|x1-x2|·
==.
∵-1<a<且a≠0,
∴当a=-时,S△OAB有最大值,S△OAB无最小值.
(3)由题意可知
f(x)-g(x)=a(x-p)(x-q).
∵0<x<p<q<,
∴a(x-p)(x-q)>0,
∴当x∈(0,p)时,f(x)-g(x)>0,
即f(x)>g(x).
又f(x)-(p-a)=a(x-p)(x-q)+x-a-(p-a)=(x-p)(ax-aq+1),
∴x-p<0,且ax-aq+1>1-aq>0,
∴f(x)-(p-a)<0,∴f(x)<p-a.
综上可知,g(x)<f(x)<p-a.
14.设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2<.
(1)当x∈(0,x1)时,证明x<f(x)<x1.
(2)设函数f(x)的图象关于直线x=x0对称,证明:x0<.
解:(1)令F(x)=f(x)-x,因为x1,x2是方程f(x)-x=0的根,∴F(x)=a(x-x1)(x-x2),当x∈(0,x1)时
∵x1<x2得(x-x1)(x-x2)>0又a>0得
F(x)=a(x-x1)(x-x2)>0即x<f(x)
x1-f(x)=x1-a(x-x1)(x-x2)-x=(x1-x)[1+a(x-x2)]
∵x1-x>0,1+a(x-x2)=1+ax-ax2>1-ax2>0
∴x1-f(x)>0,∴f(x)<x1,∴x<f(x)<x1
(2)依题意知x0=-,∵x1,x2是方程f(x)-x=0的根,即x1,x2是方程ax2+(b-1)x+c=0的根
∴x1+x2=-,x0=-==
∵ax2<1,∴x0<=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com