
8. 设函数f (x)=x3+ax2+bx-1,若当x=1时,有极值为1,则函数g(x)=x3+ax2+bx的单调递减区间为 .
7.设l1为曲线y1=sinx在点(0,0)处的切线,l2为曲线y2=cosx在点( ,0)处的切线,则l1与l2的夹角为___________.
,0)处的切线,则l1与l2的夹角为___________.
6. 函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、最小值分别是( )
(A)1,-1 (B)3,-17 (C)1,-17 (D)9,-19
5. y=2x3-3x2+a的极大值为6,那么a等于( )
(A)6 (B)0 (C)5 (D)1
4. 函数 在下面哪个区间内是增函数( ).
在下面哪个区间内是增函数( ).
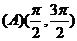


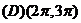
3. C设S上的切点 求导数得斜率,过点P可求得:
求导数得斜率,过点P可求得: .
.
2. 已知曲线S:y=3x-x3及点 ,则过点P可向S引切线的条数为( )
,则过点P可向S引切线的条数为( )
(A)0 (B)1 (C)2 (D)3
1. 设函数f(x)在定义域内可导,y=f(x)的图象如右图所示,则导函数y=f ¢(x)的图象可能为( )

14.(1)一物体按规律x=bt3作直线运动,式中x为时间t内通过的距离,媒质的阻力正比于速度的平方.试求物体由x=0运动到x=a时,阻力所作的功。
(2)抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a、b值,并求Smax.
典型例题
一 导数的概念与运算
EG:如果质点A按规律s=2t3运动,则在t=3 s时的瞬时速度为( )
A. 6m/s B. 18m/s C. 54m/s D. 81m/s
变式:定义在D上的函数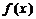 ,如果满足:
,如果满足: ,
, 常数
常数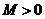 ,
,
都有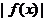 ≤M成立,则称
≤M成立,则称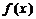 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
[文](1)若已知质点的运动方程为 ,要使在
,要使在 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
[理](2)若已知质点的运动方程为 ,要使在
,要使在 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
EG:已知 的值是( )
的值是( )
A.
 B.
2 C.
B.
2 C.  D. -2
D. -2
变式1: ( )
( )
A.-1 B.-2 C.-3 D.1
变式2: ( )
( )
A. B.
B. C.
C. D.
D.
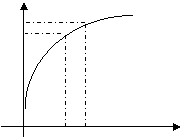
根据所给的函数图像比较
变式:函数 的图像如图所示,下列数值排序正确的是( )
的图像如图所示,下列数值排序正确的是( )
 A.
A.  y
y
B. 
C. 
D.  O 1
2 3 4 x
O 1
2 3 4 x
EG:求所给函数的导数:
 。
。
变式:设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时, >0.且g(3)=0.则不等式f(x)g(x)<0的解集是
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
EG:已知函数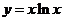 .(1)求这个函数的导数;(2)求这个函数在点
.(1)求这个函数的导数;(2)求这个函数在点 处的切线的方程.
处的切线的方程.
变式1:已知函数 .
.
(1)求这个函数在点 处的切线的方程;
处的切线的方程;
(2)过原点作曲线y=ex的切线,求切线的方程.
变式2:函数y=ax2+1的图象与直线y=x相切,则a=( )
A.  B.
B.  C.
C. 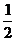 D. 1
D. 1
EG:判断下列函数的单调性,并求出单调区间:

变式1:函数 的一个单调递增区间是
的一个单调递增区间是
A. B.
B.  C.
C.  D.
D. 
变式2:已知函数
(1)若函数的单调递减区间是(-3,1),则 的是 .
的是 .
(2)若函数在 上是单调增函数,则
上是单调增函数,则 的取值范围是
.
的取值范围是
.
变式3: 设 ,点P(
,点P( ,0)是函数
,0)是函数 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
EG:求函数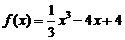 的极值.
的极值.
求函数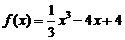 在
在 上的最大值与最小值..
上的最大值与最小值..
变式1: 函数 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间 内有极小值点( )
内有极小值点( )
 A.1个
A.1个
B.2个
C.3个
D.4个
变式2:已知函数 在点
在点 处取得极大值
处取得极大值 ,其导函数
,其导函数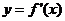 的图象经过点
的图象经过点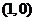 ,
, ,如图所示.求:
,如图所示.求:
 (Ⅰ)
(Ⅰ) 的值;(Ⅱ)
的值;(Ⅱ) 的值.
的值.
变式3:若函数 ,当
,当 时,函数
时,函数 极值
极值 ,
,
(1)求函数的解析式;
(2)若函数 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.
变式4:已知函数 ,对xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范围。
,对xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范围。
EG:利用函数的单调性,证明:
变式1:证明: ,
,
变式2:(理科)设函数f(x)=(1+x)2-ln(1+x)2.若关于x的方程f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,求实数a的取值范围.
EG: 函数 若
若 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
变式1:设函数 若
若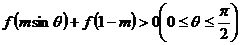 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
变式2:如图,曲线段OMB是函数 的图象,
的图象, 轴于点A,曲线段OMB上一点M
轴于点A,曲线段OMB上一点M 处的切线PQ交x轴于点P,交线段AB于点Q,
处的切线PQ交x轴于点P,交线段AB于点Q,
(1)若t已知,求切线PQ的方程 (2)求 的面积的最大值
的面积的最大值
变式3:用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻折900角,再焊接而成,问该容器的高为多少时,容器的容积最大?最大的容积是多少?
变式4:某厂生产某种产品 件的总成本
件的总成本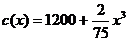 (万元),已知产品单价的平方与产品件数
(万元),已知产品单价的平方与产品件数 成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
EG:计算下列定积分:(理科定积分、微积分)

变式1:计算:;
(1)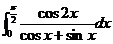 ;(2)
;(2)
变式2: 求将抛物线 和直线
和直线 围成的图形绕
围成的图形绕 轴旋转一周得到的几何体的体积.
轴旋转一周得到的几何体的体积.
变式3:在曲线 上某一点A处作一切线使之与曲线以及
上某一点A处作一切线使之与曲线以及 轴所围的面积为
轴所围的面积为 ,试求:(1)切点A的坐标;(2)在切点A的切线方程.
,试求:(1)切点A的坐标;(2)在切点A的切线方程.
实战训练
13.计算下列定积分的值
(1)
(2) ;
;
(3) ;
;
(4)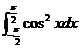 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com