
4.曲线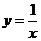 和
和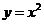 在它们交点处的两条切线与
在它们交点处的两条切线与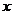 轴所围成的三角形面积是
。
轴所围成的三角形面积是
。
3.过点(-1,0)作抛物线 的切线,则其中一条切线为
的切线,则其中一条切线为
2.若曲线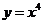 的一条切线
的一条切线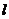 与直线
与直线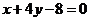 垂直,则
垂直,则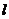 的方程为
的方程为
1.求下列函数导数
(1)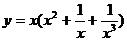 (2)
(2)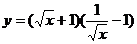
(3) (4)y=
(4)y=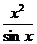
3.最值:
一般地,在区间[a,b]上连续的函数f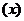 在[a,b]上必有最大值与最小值。
在[a,b]上必有最大值与最小值。
①求函数ƒ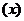 在(a,b)内的极值;
在(a,b)内的极值;
②求函数ƒ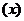 在区间端点的值ƒ(a)、ƒ(b);
在区间端点的值ƒ(a)、ƒ(b);
③将函数ƒ 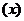 的各极值与ƒ(a)、ƒ(b)比较,其中最大的是最大值,其中最小的是最小值。
的各极值与ƒ(a)、ƒ(b)比较,其中最大的是最大值,其中最小的是最小值。
课前预习
2.极点与极值:
曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
1.单调区间:一般地,设函数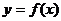 在某个区间可导,
在某个区间可导,
如果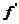
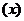
 ,则
,则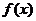 为增函数; 如果
为增函数; 如果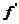
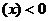 ,则
,则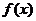 为减函数;
为减函数;
如果在某区间内恒有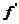
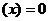 ,则
,则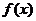 为常数;
为常数;
4.两个函数的和、差、积的求导法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即:
(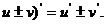
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: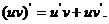
若C为常数,则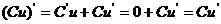 .即常数与函数的积的导数等于常数乘以函数的导数:
.即常数与函数的积的导数等于常数乘以函数的导数: 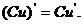
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: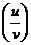 ‘=
‘=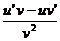 (v
(v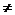 0)。
0)。
形如y=f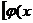
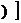 的函数称为复合函数。复合函数求导步骤:分解--求导--回代。法则:y'|
的函数称为复合函数。复合函数求导步骤:分解--求导--回代。法则:y'|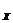 = y'|
= y'|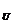 ·u'|
·u'|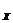
导数应用
知识清单
3.几种常见函数的导数:
① ②
②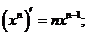 ③
③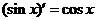 ; ④
; ④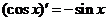 ;
;
⑤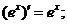 ⑥
⑥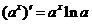 ; ⑦
; ⑦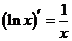 ; ⑧
; ⑧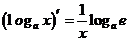 .
.
2.导数的几何意义
函数y=f(x)在点x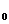 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x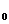 ,f(x
,f(x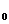 ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x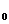 ,f(x
,f(x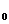 ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x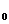 )。相应地,切线方程为y-y
)。相应地,切线方程为y-y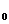 =f/(x
=f/(x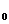 )(x-x
)(x-x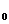 )。
)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com