
3. I like this house with a
beautiful garden in front , but I don’t have enough money to buy__________.
A. one B. it C. this D. that
2. He told us whether
_________ a picnic was still under discussion
A. to have B. having C. have D. had
第一节
语法和词汇知识(共20小题;每小题1分,满分20分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
1. -May
I open the window to let in some fresh air ?
-___________
A. Come on B. Take care C. Go ahead! D. Hold on!
3.导数与解析几何或函数图象的混合问题是一种重要类型,也是高考中考察综合能力的一个方向,应引起注意。
2.关于函数特征,最值问题较多,所以有必要专项讨论,导数法求最值要比初等方法快捷简便。
4.导数的常规问题:
(1)刻画函数(比初等方法精确细微);
(2)同几何中切线联系(导数方法可用于研究平面曲线的切线);
(3)应用问题(初等方法往往技巧性要求较高,而导数方法显得简便)等关于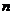 次多项式的导数问题属于较难类型。
次多项式的导数问题属于较难类型。
3.导数的应用:
①求切线的斜率。
②导数与函数的单调性的关系
㈠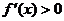 与
与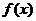 为增函数的关系。
为增函数的关系。
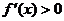 能推出
能推出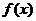 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数 在
在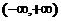 上单调递增,但
上单调递增,但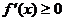 ,∴
,∴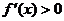 是
是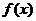 为增函数的充分不必要条件。
为增函数的充分不必要条件。
㈡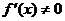 时,
时,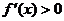 与
与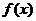 为增函数的关系。
为增函数的关系。
若将 的根作为分界点,因为规定
的根作为分界点,因为规定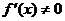 ,即抠去了分界点,此时
,即抠去了分界点,此时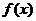 为增函数,就一定有
为增函数,就一定有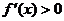 。∴当
。∴当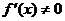 时,
时,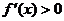 是
是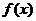 为增函数的充分必要条件。
为增函数的充分必要条件。
㈢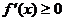 与
与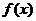 为增函数的关系。
为增函数的关系。
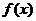 为增函数,一定可以推出
为增函数,一定可以推出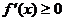 ,但反之不一定,因为
,但反之不一定,因为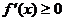 ,即为
,即为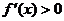 或
或 。当函数在某个区间内恒有
。当函数在某个区间内恒有 ,则
,则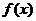 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴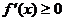 是
是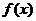 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,要谨慎处理。
㈣单调区间的求解过程,已知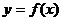 (1)分析
(1)分析 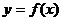 的定义域;(2)求导数
的定义域;(2)求导数 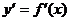 (3)解不等式
(3)解不等式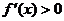 ,解集在定义域内的部分为增区间(4)解不等式
,解集在定义域内的部分为增区间(4)解不等式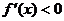 ,解集在定义域内的部分为减区间。
,解集在定义域内的部分为减区间。
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数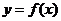 在某个区间内可导。
在某个区间内可导。
③求极值、求最值。
注意:极值≠最值。函数f(x)在区间[a,b]上的最大值为极大值和f(a) 、f(b)中最大的一个。最小值为极小值和f(a) 、f(b)中最小的一个。
f/(x0)=0不能得到当x=x0时,函数有极值。
但是,当x=x0时,函数有极值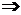 f/(x0)=0
f/(x0)=0
判断极值,还需结合函数的单调性说明。
2.导数的几何物理意义:
k=f/(x0)表示过曲线y=f(x)上的点P(x0,f(x0))的切线的斜率。
V=s/(t) 表示即时速度。a=v/(t) 表示加速度。
1.求导法则:
(c)/=0 这里c是常数。即常数的导数值为0。
(xn)/=nxn-1 特别地:(x)/=1 (x-1)/= (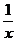 )/=-x-2 (f(x)±g(x))/= f/(x)±g/(x) (k•f(x))/=
k•f/(x)
)/=-x-2 (f(x)±g(x))/= f/(x)±g/(x) (k•f(x))/=
k•f/(x)
A 组
(1)设曲线在某点的切线斜率为负数,①则此切线的倾斜角( ),
②曲线在该点附近的变化趋势是( )
①(A) 小于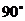 (B) 大于
(B) 大于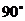 (C) 小于或等于
(C) 小于或等于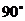 (D) 大于或等于
(D) 大于或等于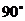
②(A)单调递增 (B)单调递减 (C)无变化 (D)以上均有可能
(2) ①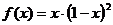 有( )个极值点; ②
有( )个极值点; ②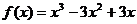 有( )个极值点
有( )个极值点
(A) 0 (B)1 (C)2 (D) 3
(3)如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与时间t的关系,




(1) (2) (3) (4)


 h
h
h
h
h
h
h
h






 t t
t
t
t t
t
t
(a) (b) (c) (d)
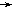
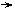
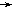
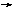
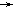
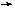
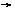 A.(1) (c)
(2) (a) (3)
(b) (4) (d) B. (1) (c)
(2) (b) (3)
(a) (4) (d)
A.(1) (c)
(2) (a) (3)
(b) (4) (d) B. (1) (c)
(2) (b) (3)
(a) (4) (d)

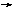
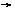
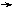
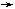
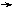 C.(1) (c) (2)
(d) (3) (a)
(4) (b) D. (1) (c)
(2) (a) (3)
(d) (4) (b)
C.(1) (c) (2)
(d) (3) (a)
(4) (b) D. (1) (c)
(2) (a) (3)
(d) (4) (b)
(4)一个距地心距离为r,质量为m的人造卫星,与地球之间的万有引力F由公式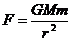 给出,其中M为地球质量,G为常量,求F对于r的瞬时变化率为
.
给出,其中M为地球质量,G为常量,求F对于r的瞬时变化率为
.
(5)一杯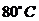 的热红茶置于
的热红茶置于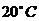 的房间里,它的温度会逐渐下降,温度
的房间里,它的温度会逐渐下降,温度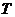 (单位
(单位 )与时间
)与时间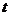 (单位:min)之间的关系由函数
(单位:min)之间的关系由函数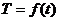 给出,则①
给出,则①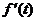 的符号为
;
的符号为
;
②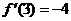 的实际意义是 .
的实际意义是 .
(6) 已知圆面积为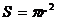 ,利用导数的定义求
,利用导数的定义求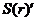 ,试解释其意义.
,试解释其意义.
(7)①求函数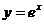 在
在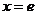 处的切线的方程;②过原点作曲线y=ex的切线,求切线的方程.
处的切线的方程;②过原点作曲线y=ex的切线,求切线的方程.
(8)已知函数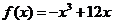 ,①求函数的单调区间;②求函数的极值,并画出函数的草图;③当
,①求函数的单调区间;②求函数的极值,并画出函数的草图;③当 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.
(9)欲制作一个容积为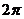 立方米的圆柱形储油罐(有盖),问它的底面半径与高分别为多少时,才能使所用的材料最省?
立方米的圆柱形储油罐(有盖),问它的底面半径与高分别为多少时,才能使所用的材料最省?
(10)利用函数的单调性,证明下列不等式,并通过函数图像直观验证: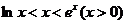
(11)函数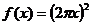 的导数是( )
的导数是( )
(A) 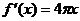 (B)
(B) 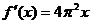 (C)
(C) 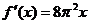 (D)
(D) 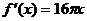
(12)函数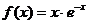 的一个单调递增区间是
的一个单调递增区间是
(A)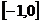 (B)
(B) 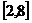 (C)
(C) 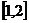 (D)
(D) 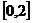
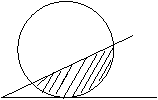
 (13)如图,直线
(13)如图,直线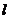 和圆C,当
和圆C,当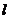 从
从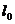 开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过
开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过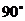 )时,它扫过的圆内阴影部分的面积S是时间t的函数,这个函数图象大致是(画草图)
)时,它扫过的圆内阴影部分的面积S是时间t的函数,这个函数图象大致是(画草图)
 C
C
 S
S
O
 O
t
O
t
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com