
12.(Ⅰ)将一颗骰子掷n(n≥2)次,求所得点数的最大值为5且最小值为2的概率.
(Ⅱ)A、B二人拿两枚骰子做抛掷游戏,规则如下:若掷出的点数之和为3的倍数时,原掷骰子的人继续掷;若掷出的不是3的倍数时,就由对方接着掷.第一次由A掷.
(1)记第n次由A掷的概率为Pn,求Pn;
(2)求前4次抛掷中A恰好掷3次的概率.
分析(Ⅰ) 在计算本例概率时要明白在掷了n次骰子后,6点与l点均不出现.但是5点和2点均要出现,根据此并利用间接法即可求得本例的概率.
掷n次骰子,不出现1点与6点的概率是(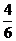 )n=(
)n=(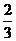 )n;
)n;
掷n次骰子,不出现1点、6点及5点的概率是(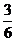 )n=(
)n=(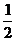 )n;
)n;
掷n次骰子,不出现1点、6点及2点的概率是(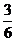 )n=(
)n=(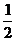 )n;
)n;
掷n次骰子,不出现1点、6点、2点及5点的概率是(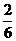 )n=(
)n=(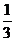 )n.
)n.
掷n次骰子,所得的点数的最大值为5且最小值为2的情况应该是不出现1点与6点,并且要出现2点与5点.因此,所求的概率为
(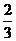 )n - (
)n - (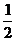 )n - (
)n - (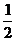 )n + (
)n + (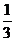 )n =
)n = 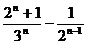 .
.
分析(Ⅱ):(1)第n+1次由A掷的事件由两个互斥事件组成:
①“第n次由A掷,第n+1次仍由A掷”,此时概率为 Pn;
Pn;
②“第n次由B掷,第n+1次由A掷”,此时概率为(1- )(1-Pn)=
)(1-Pn)=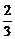 (1-Pn).于是,Pn+1=
(1-Pn).于是,Pn+1= Pn+
Pn+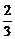 (1-Pn),整理得Pn+1-
(1-Pn),整理得Pn+1-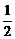 =-
=- (Pn-
(Pn-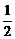 ).
).
数列{Pn-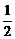 }是以
}是以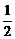 为首项,公比为-
为首项,公比为- 的等比数列,即Pn=
的等比数列,即Pn=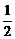 +
+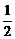 (-
(- )n-1.6分
)n-1.6分
(2)事件“前4次抛掷中A恰好掷3次”由三个彼此互斥的事件所组成:
①“第1,2,4次A掷,第3次B掷”(即AABA);
②“第1,3,4次A掷,第2次B掷”(即ABAA);
③“第1,2,3次A掷,第4次B掷”(即AAAB).
于是,前4次抛掷中A恰好掷3次的概率P=P(AABA)+P(ABAA)+P(AAAB)=1× ×
×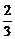 ×
×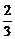 +1×
+1×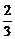 ×
×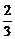 ×
× +1×
+1× ×
× ×
×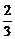 =
=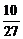 .
.
11.在一次智力竞赛中,比赛共分三个环节:选答、抢答、风险选答。第一环节“选答”中,每位选手可以从6道题目(其中4道选择题、2道操作题)中任意选3道题目作答,答对每道题目可得100分;第二环节“抢答”中,一共为参赛选手准备了5道抢答题,在每一道题目的抢答中,每位选手抢到的概率是相等的;在第三环节“风险选答”中,一共为选手准备了A、B、C三类不同的题目,选手每答对一道A类、B类、C类的题目,将分别得到300分、200分、100分,但如果答错,则相应地要扣去300分、200分、100分,而选手答对一道A类、B类、C类题目的概率分别为0.6,0.7,0.8,现在甲、乙、丙三位选手参加比赛,试求:
(1) 乙选手在第一环节中至少选到一道操作题的概率是多少?
(2) 在第二环节中,甲选手抢到的题目多于乙选手而不多于丙选手的概率是多少?
(3) 在第三环节中,就每一次答题而言,丙选手选择哪类题目得分的期望值更大一些?
答:(1)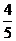 ;(2)
;(2)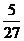 ;(3)选B类题
;(3)选B类题
10.袋中装有m个红球和n个白球,m≥n≥2,这些红球和白球除了颜色不同以外,其余都相同。从袋中同时取出2个球。
(1)若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍,试证:m必为奇数;
(2)在m,n的数组中,若取出的球是同色的概率等于不同色的概率,试求m+n≤40的所有数组(m,n)
答:(2)(6,3),(10,6),(15,10),(21,15)
9.在排球比赛中,使用的规则是“五局三胜”制,即最多打五局,有一个队胜三局则为胜方,在每局比赛中,A、B两队获胜的概率分别为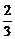 、
、 ,则最终B队获胜的概率是___
,则最终B队获胜的概率是___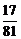 ____.
____.
8.一个盒子中有9个正品和3个废品,每次取1个产品,取出后不再放回,在取得正品前已取出的废品数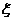 的期望
的期望 = 0.3
= 0.3
7.若以连续掷两次骰子所得的点数m、n为点P的坐标,且点P落在圆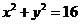 的内部的概率
的内部的概率 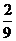
6.已知随机变量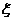 只能取3个值:
只能取3个值: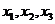 ,其概率依次成等差数列,则这个数列的公差的取值范围是(C )
,其概率依次成等差数列,则这个数列的公差的取值范围是(C )
A.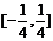 B.
B.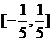 C.
C.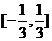 D.
D.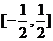
5.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( A )
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
4.如图,某城镇由6条东西方向的街道和6条南北方向的街道组成,
其中有一个池塘,街道在此变成一个菱形的环池大道。现要从城镇
的A处走到B处,使所走的路程最短最多可以有 35 种不同
的走法。
3.由0,1,2,3,4这五个数组成的无重复数字的四位偶数,按从小到大的顺序排成一个数列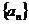 ,则
,则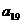 = 2014
。
= 2014
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com