
5.已知集合A=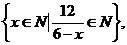 用列举法表示集合A=
用列举法表示集合A= 
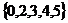
6 已知U=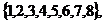
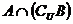
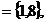
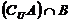
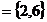
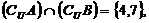 则集合A=
则集合A=


4.不等式|x-1|>-3的解集是
 ®
®
3.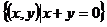
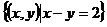 集合P= ,Q= ,则A∩B=
集合P= ,Q= ,则A∩B= 
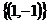

1.课本P12练习(1-5) 2.课本P13 练习(1-4) 
例1(课本第12页)设U={1,2,3,4,5,6,7,8},A={3,4,5},B={4,7,8},求CuA,
CuB, (CuA)  (CuB),
(CuA)
(CuB),
(CuA)  (CuB),
Cu(A
(CuB),
Cu(A B) , Cu(A
B) , Cu(A B).
B).
解:CuA={1,2,6,7,8} CuB={1,2,3,5,6}
(CuA)
 (CuB)= Cu(A
(CuB)= Cu(A B)={1,2,6}
B)={1,2,6}
(CuA)
 (CuB)= Cu(A
(CuB)= Cu(A B)={1,2,3,5,6,7,8}
B)={1,2,3,5,6,7,8}
例2 已知集合A={y|y=x2-4x+5},B={x|y=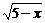 }求A∩B,A∪B.
}求A∩B,A∪B.
解:A∩B= {x|1≤x≤5}, A∪B=R.
例3 已知A={x|x2≤4}, B={x|x>a},若A∩B=Ф,求实数a的取值范围.
解:a≧2
例4 集合M={(x,y) |∣xy∣=1,x>0},N={(x,y) |xy=-1},求M∪N.
解:M∪N={(x,y) |xy=-1,或xy=1(x>0)}.
例5 已知全集U={x|x2-3x+2≥0},A={x||x-2|>1},B=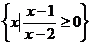 ,
,
求CUA,CUB,A∩B,A∩(CUB),(CUA)∩B
解:∵U={x|x2-3x+2≥0}={x|x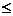 1或x
1或x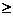 2},
2},
A={x||x-2|>1}={x|x<1或x>3},
B=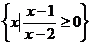 ={x| x
={x| x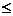 1或x>2}
1或x>2}
∴CUA=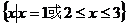
CUB=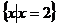
A∩B=A={x|x<1或x>3},={x|x<1或x>3},
A∩(CUB)=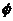
(CUA)∩B=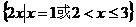
3. 德摩根律:(CuA)  (CuB)= Cu (A
(CuB)= Cu (A B),
B),
(CuA)
 (CuB)= Cu(A
(CuB)= Cu(A B)(可以用韦恩图来理解).
B)(可以用韦恩图来理解).
结合补集,还有①A (CuA)=U, ②A
(CuA)=U, ②A (CuA)=
Φ.
(CuA)=
Φ.
容斥原理
一般地把有限集A的元素个数记作card(A).对于两个有限集A,B,有
card(A∪B)= card(A)+card(B)- card(A∩B).
2.并集的性质
(1)A A=A (2)A
A=A (2)A Φ=A (3)A
Φ=A (3)A B=B
B=B A (4)A
A (4)A B
B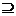 A,A
A,A B
B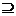 B
B
联系交集的性质有结论:Φ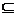 A
A B
B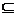 A
A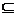 A
A B.
B.
 交集、并集的性质
交集、并集的性质
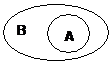 用文图表示
用文图表示
(1)若A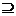 B,则A
B,则A B=B, A
B=B, A B=B
B=B
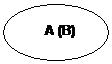 (2)若A
(2)若A B则A
B则A B=A A
B=A A B=A
B=A
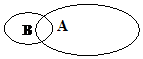 (3)若A=B, 则A
(3)若A=B, 则A A=A A
A=A A A=A
A=A
(4)若A,B相交,有公共元素,但不包含
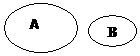 则A
则A B
B  A,A
A,A B
B B
B
A B
B A, A
A, A B
B B
B
(5) )若A,B无公共元素,则A B=Φ
B=Φ
(学生思考、讨论、分析:从图中你能看出那些结论?):
从图中观察分析、思考、讨论,完全归纳以下性质,并用集合语言证明:
1.交集的性质
(1)A A=A A
A=A A Φ=ΦA
Φ=ΦA B=B
B=B A
(2)A
A
(2)A B
B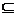 A, A
A, A B
B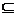 B.
B.
2.并集的定义
一般地,由所有属于A或属于B的元素所组成的集合,叫做A,B的并集.
记作:A B(读作‘A并B’),即A
B(读作‘A并B’),即A B ={x|x
B ={x|x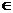 A,或x
A,或x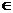 B}).
B}).
1.交集的定义
一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.
记作A B(读作‘A交B’),即A
B(读作‘A交B’),即A B={x|x
B={x|x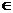 A,且x
A,且x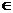 B}.
B}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com