
4.函数y=ksinx+b的最大值为2, 最小值为-4,求k,b的值
解:当k>0时 
当k<0时  (矛盾舍去) ∴k=3
b=-1
(矛盾舍去) ∴k=3
b=-1
3. 求下列函数的最值:
1° y=sin(3x+ )-1 2°
y=sin2x-4sinx+5 3° y=
)-1 2°
y=sin2x-4sinx+5 3° y=
解:1° 当3x+ =2kp+
=2kp+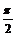 即 x=
即 x= (kÎZ)时ymax=0
(kÎZ)时ymax=0
当3x+ =2kp-
=2kp-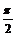 即x=
即x= (kÎZ)时ymin=-2
(kÎZ)时ymin=-2
2° y=(sinx-2)2+1 ∴当x=2kp-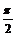 kÎZ时ymax=10
kÎZ时ymax=10
当x=2kp-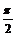 kÎZ时ymin=
2
kÎZ时ymin=
2
3° y=-1+ 当x=2kp+p kÎZ时
ymax=2
当x=2kp+p kÎZ时
ymax=2
当x=2kp kÎZ时
ymin= 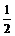
2. 直接写出下列函数的定义域、值域:
1° y= 2° y=
2° y=
解:1°当x¹2kp-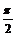 kÎZ时函数有意义,值域:[
kÎZ时函数有意义,值域:[ +∞]
+∞]
2 °xÎ[2kp+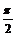 , 2kp+
, 2kp+ ] (kÎZ)时有意义,
值域[0,
] (kÎZ)时有意义,
值域[0,  ]
]
1.求下列函数的周期:
1°y=sin(2x+ )+2cos(3x-
)+2cos(3x- ) 2° y=|sinx| 3° y=2
) 2° y=|sinx| 3° y=2 sinxcosx+2cos2x-1
sinxcosx+2cos2x-1
解:1° y1=sin(2x+ ) 最小正周期T1=p
) 最小正周期T1=p
y2=2cos(3x- ) 最小正周期 T2=
) 最小正周期 T2=
∴T为T1 ,T2的最小公倍数2p ∴T=2p
2° T=p
3° y= sin2x+cos2x ∴T=p
sin2x+cos2x ∴T=p
例1 求使下列函数取得最大值的自变量x的集合,并说出最大值是什么
(1)y=cosx+1,x∈R;
(2)y=sin2x,x∈R
解:(1)使函数y=cosx+1,x∈R取得最大值的x的集合,就是使函数y=cosx,x∈R取得最大值的x的集合{x|x=2kπ,k∈Z}
函数y=cosx+1,x∈R的最大值是1+1=2
(2)令Z=2x,那么x∈R必须并且只需Z∈R,且使函数y=sinZ,Z∈R取得最大值的Z的集合是{Z|Z= +2kπ,k∈Z}
+2kπ,k∈Z}
由2x=Z= +2kπ,
+2kπ,
得x= +kπ
+kπ
即 使函数y=sin2x,x∈R取得最大值的x的集合是{x|x= +kπ,k∈Z}
+kπ,k∈Z}
函数y=sin2x,x∈R的最大值是1
例2求下列函数的定义域:
(1)y=1+ (2)y=
(2)y=
解:(1)由1+sinx≠0,得sinx≠-1
即x≠ +2kπ(k∈Z)
+2kπ(k∈Z)
∴原函数的定义域为{x|x≠ +2kπ,k∈Z}
+2kπ,k∈Z}
(2)由cosx≥0得- +2kπ≤x≤
+2kπ≤x≤ +2kπ(k∈Z)
+2kπ(k∈Z)
∴原函数的定义域为[- +2kπ,
+2kπ, +2kπ](k∈Z)
+2kπ](k∈Z)
 例3求函数y=-cosx的单调区间
例3求函数y=-cosx的单调区间
解:由y=-cosx的图象可知:
单调增区间为[2kπ,(2k+1)π](k∈Z)
单调减区间为[(2k-1)π,2kπ](k∈Z)
例4求下列三角函数的周期:1° y=sin(x+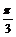 ) 2°
y=cos2x 3° y=3sin(
) 2°
y=cos2x 3° y=3sin( +
+ )
)
解:1° 令z=
x+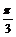 而 sin(2p+z)=sinz 即:f (2p+z)=f (z)
而 sin(2p+z)=sinz 即:f (2p+z)=f (z)
f [(x+2p)+ 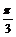 ]=f (x+
]=f (x+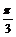 ) ∴周期T=2p
) ∴周期T=2p
2°令z=2x ∴f (x)=cos2x=cosz=cos(z+2p)=cos(2x+2p)=cos[2(x+p)]
即:f (x+p)=f (x) ∴周期T=p
3°令z= +
+ 则
则
f (x)=3sinz=3sin(z+2p)=3sin( +
+ +2p)=3sin(
+2p)=3sin( )=f (x+4p)
)=f (x+4p)
∴周期T=4p
(1)定义域:
正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)],
分别记作:
y=sinx,x∈R
y=cosx,x∈R
(2)值域
因为正弦线、余弦线的长度小于或等于单位圆的半径的长度,所以|sinx|≤1,|cosx|≤1,即
-1≤sinx≤1,-1≤cosx≤1
也就是说,正弦函数、余弦函数的值域都是[-1,1]
其中正弦函数y=sinx,x∈R
①当且仅当x= +2kπ,k∈Z时,取得最大值1
+2kπ,k∈Z时,取得最大值1
②当且仅当x=- +2kπ,k∈Z时,取得最小值-1
+2kπ,k∈Z时,取得最小值-1
而余弦函数y=cosx,x∈R
①当且仅当x=2kπ,k∈Z时,取得最大值1
②当且仅当x=(2k+1)π,k∈Z时,取得最小值-1
(3)周期性
由sin(x+2kπ)=sinx,cos(x+2kπ)=cosx (k∈Z)知:
正弦函数值、余弦函数值是按照一定规律不断重复地取得的
一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期
由此可知,2π,4π,……,-2π,-4π,……2kπ(k∈Z且k≠0)都是这两个函数的周期
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期
注意:
1°周期函数xÎ定义域M,则必有x+TÎM, 且若T>0则定义域无上界;T<0则定义域无下界;
2°“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)¹f (x0))
3°T往往是多值的(如y=sinx 2p,4p,…,-2p,-4p,…都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期)
根据上述定义,可知:正弦函数、余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π
(4)奇偶性
由sin(-x)=-sinx
cos(-x)=cosx
可知:y=sinx为奇函数
y=cosx为偶函数
∴正弦曲线关于原点O对称,余弦曲线关于y轴对称
(5)单调性
从y=sinx,x∈[- ]的图象上可看出:
]的图象上可看出:
当x∈[- ,
, ]时,曲线逐渐上升,sinx的值由-1增大到1
]时,曲线逐渐上升,sinx的值由-1增大到1
当x∈[ ,
, ]时,曲线逐渐下降,sinx的值由1减小到-1
]时,曲线逐渐下降,sinx的值由1减小到-1
结合上述周期性可知:
正弦函数在每一个闭区间[- +2kπ,
+2kπ, +2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[
+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[ +2kπ,
+2kπ, +2kπ](k∈Z)上都是减函数,其值从1减小到-1
+2kπ](k∈Z)上都是减函数,其值从1减小到-1
余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1
4.用正弦函数和余弦函数的图象解最简单的三角不等式
3.用五点法作正弦函数和余弦函数的简图(描点法):
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:
(0,0) (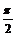 ,1) (p,0) (
,1) (p,0) ( ,-1) (2p,0)
,-1) (2p,0)
(1)y=cosx,
xÎR与函数y=sin(x+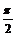 ) xÎR的图象相同
) xÎR的图象相同
(2)将y=sinx的图象向左平移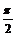 即得y=cosx的图象
即得y=cosx的图象
 (3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是
(3)也同样可用五点法作图:y=cosx xÎ[0,2p]的五个点关键是
(0,1) (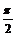 ,0) (p,-1) (
,0) (p,-1) ( ,0) (2p,1)
,0) (2p,1)
2.用单位圆中的正弦线、余弦线作正弦函数y=sinx,x∈[0,2π]、余弦函数y=cosx,x∈[0,2π]的图象(几何法):

把y=sinx,x∈[0,2π]和y=cosx,x∈[0,2π]的图象,沿着x轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx,x∈R和y=cosx,x∈R的图象,分别叫做正弦曲线和余弦曲线.


1. 正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M,则有
 ,
,
向线段MP叫做角α的正弦线,有向线段OM叫做角α的余弦线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com