
9.学校餐厅供应客饭,每位学生可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了5种不同的荤菜,若要保证每位学生有200种以上的不同选择,则餐厅至少还需准备 种不同的素菜种
8.
 位同学进行网页设计比赛,决出了第1至第5名的名次
位同学进行网页设计比赛,决出了第1至第5名的名次
 、
、 两位同学去询问名次,主考官对
两位同学去询问名次,主考官对 说:“很遗憾,你和
说:“很遗憾,你和 都未拿到冠军”;对
都未拿到冠军”;对 说:“你当然不会是最差的
说:“你当然不会是最差的 ”从这个回答分析,
”从这个回答分析, 位同学的名次排列共可能有
种不同的情况
位同学的名次排列共可能有
种不同的情况
7.赛艇运动员10人,3人会划右舷,2人会划左舷,其余5人两舷都能划,现要从中挑选6人上艇,平均分配在两舷上划桨,共有
种选法
6.有排成一行的 个空位置,
个空位置, 位女生去坐,要求任何两个女生之间都要有空位,共有 种不同的坐法
位女生去坐,要求任何两个女生之间都要有空位,共有 种不同的坐法
5.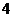 名男生和
名男生和 名女生排成一行,按下列要求各有多少种排法:
名女生排成一行,按下列要求各有多少种排法:
(1)男生必须排在一起 ; (2)女生互不相邻 ;
(3)男女生相间 ; (4)女生按指定顺序排列 .
4.公共汽车上有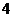 位乘客,汽车沿途停靠
位乘客,汽车沿途停靠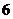 个站,那么这
个站,那么这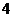 位乘客不同的下车方式共有 种;如果其中任何两人都不在同一站下车,那么这
位乘客不同的下车方式共有 种;如果其中任何两人都不在同一站下车,那么这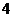 位乘客不同的下车方式共有 种
位乘客不同的下车方式共有 种
3.3名医生和6名护士被分配到3所学校为学生体检,每所学校分配1名医生和2名护士,不同的分配方法共有( )
 .
.
 .
.
 .
.
 .
.
2.学校召开学生代表大会,高二年级的3个班共选6名代表,每班至少1名,代表的名额分配方案种数是 ( )
 .
.
 .
.
 .
.
 .
.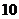
1.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点 向结点
向结点 传递信息,信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为 ( )
传递信息,信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为 ( )
 .
.
 .
.
 .
.
 .
.
例1.某考生打算从 所重点大学中选
所重点大学中选 所填在第一档次的
所填在第一档次的 个志愿栏内,其中
个志愿栏内,其中 校定为第一志愿;再从
校定为第一志愿;再从 所一般大学中选
所一般大学中选 所填在第二档次的三个志愿栏内,其中
所填在第二档次的三个志愿栏内,其中 、
、 两校必选,且
两校必选,且 在
在 前
前 问:此考生共有多少种不同的填表方法?
问:此考生共有多少种不同的填表方法?
 解:先填第一档次的三个志愿栏:因
解:先填第一档次的三个志愿栏:因 校定为第一档次的第一志愿,故第一档次的二、三志愿有
校定为第一档次的第一志愿,故第一档次的二、三志愿有 种填法;再填第二档次的三个志愿栏:
种填法;再填第二档次的三个志愿栏: 、
、 两校有
两校有 种填法,剩余的一个志愿栏有
种填法,剩余的一个志愿栏有 种填法
种填法 由分步计数原理知,此考生不同的填表方法共有
由分步计数原理知,此考生不同的填表方法共有

 (种)
(种)
例2.如图是由12个小正方形组成的 矩形网格,一质点沿网格线从点
矩形网格,一质点沿网格线从点 到点
到点 的不同路径之中,最短路径有
条
的不同路径之中,最短路径有
条
解: 总揽全局:把质点沿网格线从点A到点 的最短路径分为七步,其中四步向右,三步向上,不同走法的区别在于哪三步向上,
的最短路径分为七步,其中四步向右,三步向上,不同走法的区别在于哪三步向上,
因此,本题的结论是: .
.
例3.圆周上有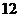 个不同的点,过其中任意两点作弦,这些弦在圆内的交点个数最多是多少?
个不同的点,过其中任意两点作弦,这些弦在圆内的交点个数最多是多少?
解:要使交点个数最多,则只需所有的交点都不重合 显然,并不是每两条弦都在圆内有交点,但如果两条弦相交,则交点就是以这两条弦的四个端点为顶点的四边形的对角线的交点,也就是说,弦在圆内的交点与以圆上四点为顶点的四边形是一一对应的
显然,并不是每两条弦都在圆内有交点,但如果两条弦相交,则交点就是以这两条弦的四个端点为顶点的四边形的对角线的交点,也就是说,弦在圆内的交点与以圆上四点为顶点的四边形是一一对应的
因此只需求以圆上四点为顶点的四边形的个数,即 个
个
变式:本题构造了四边形以求得满足条件的交点,类似的,前面讲过一个问题:
以一个正方体的8个顶点连成的异面直线共有
对
解:以一个正方体的顶点为顶点的四面体共有 =58个,每个四面体的四条棱可以组成3对异面直线,因此以一个正方体的8个顶点连成的异面直线共有3×58=174对
=58个,每个四面体的四条棱可以组成3对异面直线,因此以一个正方体的8个顶点连成的异面直线共有3×58=174对
另解: 对
对
例4.有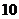 只不同的试验产品,其中有
只不同的试验产品,其中有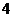 只次品,
只次品,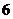 只正品,现每次取一只测试,直到
只正品,现每次取一只测试,直到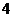 只次品全测出为止,求最后一只次品正好在第五次测试时被发现的不同情形有多少种?
只次品全测出为止,求最后一只次品正好在第五次测试时被发现的不同情形有多少种?
解:本题实质是,前五次测试中有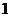 只正品
只正品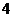 只次品,且第五次测试的是次品
只次品,且第五次测试的是次品
思路一:设想有五个位置,先从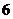 只正品中任选
只正品中任选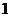 只,放在前四个位置的任一个上,有
只,放在前四个位置的任一个上,有 种方法;再把
种方法;再把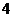 只次品在剩下的四个位置上任意排列,有
只次品在剩下的四个位置上任意排列,有 种排法
种排法 故不同的情形共有
故不同的情形共有 种
种
思路二:设想有五个位置,先从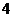 只次品中任选
只次品中任选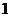 只,放在第五个位置上,有
只,放在第五个位置上,有 种方法;再从
种方法;再从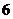 只正品中任选
只正品中任选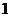 只,和剩下的
只,和剩下的 只次品一起在前四个位置上任意排列,有
只次品一起在前四个位置上任意排列,有 种方法
种方法 故不同的情形共有
故不同的情形共有 种
种
例5.在一次象棋比赛中,进行单循环比赛 其中有
其中有 人,他们各赛了
人,他们各赛了 场后,因故退出了比赛,这样,这次比赛共进行了
场后,因故退出了比赛,这样,这次比赛共进行了 场,问:比赛开始时参赛者有多少人?
场,问:比赛开始时参赛者有多少人?
解:需要考虑两种情况:第一种,因故退出比赛的两人之间没有进行比赛,则 ,此方程无正整数解;第二种,因故退出比赛的两人之间进行了比赛,则
,此方程无正整数解;第二种,因故退出比赛的两人之间进行了比赛,则 ,解得
,解得 ,所以,比赛开始时参赛者有
,所以,比赛开始时参赛者有 人
人 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com