
3. 如图所示,一长为
如图所示,一长为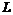 ,质量为
,质量为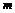 的匀质柔软链条,放在光滑的水平桌面上,有
的匀质柔软链条,放在光滑的水平桌面上,有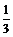 悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是多少?
悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是多少?
2.物体从高为H处自由落下,以地面为零势能面,当它的动能和势能相等时,物体离地面的高度为h,它的瞬时速度大小是v,则h和v大小为:( )
A. ,
,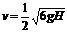 ;
;
B.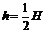 ,
,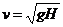 ;
;
C.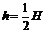 ,
,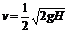 ;
;
D.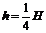 ,
,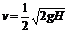 。
。
1.(南通市2008届高三基础调研测试)如图所示,某人将质量为m的石块从距地面h高处斜向上方抛出,石块抛出时的速度大小为v0,不计空气阻力,石块落地时的动能为
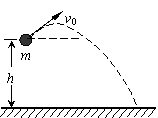 A.
A.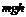
B. 
C.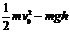
D.
4.重力做了多少正功,重力势能就减小了多少,重力做了多少负功,重力势能就增加了多少.弹力做多少功,弹性势能就增加多少,弹力做多少正功,弹性势能就减小多少.
 [应用1]如图4-3-3所示,质量为m的物体静止在地面上,物体上面连着一个轻弹簧,用手拉住弹簧上端将物体缓缓提高h,不计弹簧的质量,则人做的功应( )
[应用1]如图4-3-3所示,质量为m的物体静止在地面上,物体上面连着一个轻弹簧,用手拉住弹簧上端将物体缓缓提高h,不计弹簧的质量,则人做的功应( )
A.等于mgh B.大于mgh
C.小于mgh D.无法确定
导示: 人所做的功等于物体重力势能的增加量mgh和弹簧弹性势能的增加量总和。
故选B。
知识点二机械能守恒条件的理解
机械能守恒定律的条件:
(1)对单个物体,只有重力或弹力做功.
(2)对某一系统,物体间只有动能和重力势能及弹性势能相互转化,系统跟外界没有发生机械能的传递,机械能也没有转变成其它形式的能(如没有内能产生),则系统的机械能守恒.
(3)定律既适用于一个物体(实为一个物体与地球组成的系统),又适用于几个物体组成的物体系,但前提必须满足机械能守恒的条件.
[应用2](山东省平邑一中2007年10月阶段考试)如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间摩擦不计.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,设两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度。对于m、M和弹簧组成的系统 ( )
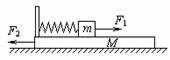 A.由于F1、F2等大反向,故系统机械能守恒
A.由于F1、F2等大反向,故系统机械能守恒
B.当弹簧弹力大小与F1、F2大小相等时,m、M各自的动能最大
C.由于F1、F2大小不变,所以m、M各自一直做匀加速运动
D.由于F1、F2均能做正功,故系统的机械能一直增大
导示:由于F1、F2对系统做功之和不为零,故系统机械能不守恒,A错误;当弹簧弹力大小与F1、F2大小相等时,速度达到最大值,故各自的动能最大,B正确;由于弹力是变化的,m、M所受合力是变化的,不会做匀加速运动,C错误;由于F1、F2先对系统做正功,当两物块速度减为零时,弹簧的弹力大于F1、F2,之后,两物块再加速相向运动,F1、F2对系统做负功,系统机械能开始减少,D错误。
答案:B。
 本题涉及到弹簧,功、机械能守恒的条件、力和运动的关系等较多知识。题目情景比较复杂,全面考查考生理解、分析、解决问题的能力。功能关系与弹簧相结合的考题在近年高考中出现得较多,复习中要加以重视。
本题涉及到弹簧,功、机械能守恒的条件、力和运动的关系等较多知识。题目情景比较复杂,全面考查考生理解、分析、解决问题的能力。功能关系与弹簧相结合的考题在近年高考中出现得较多,复习中要加以重视。

类型一单个物体机械能守恒守恒问题
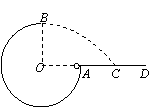 [例1](江苏省海门市2007年高三物理模拟试卷)如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,
[例1](江苏省海门市2007年高三物理模拟试卷)如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,
AD为水平面,B点在O
的正上方,一个小球
在A点以一竖直向下初速度
进入圆轨道并恰能到达B点。求:
⑴小球在A点的初速度为多少?
⑵落点C与A点的水平距离?
导示:(1)A点运动到B点,则
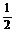 m vA2=
m vA2=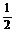 m vB2 +mg R ①
m vB2 +mg R ①
恰能通过最高点B时 mg=m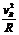 ②
②
解①②得vA =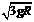 ③
③
(2)由B到C平抛运动
R=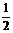 gt2 ④
gt2 ④
soc=vBt ⑤
解③④⑤得sAc= soc-R=(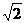 -1)R
-1)R
 对研究单个物体机械能守恒问题从能量守恒观点和转化观点进行列式解题。
对研究单个物体机械能守恒问题从能量守恒观点和转化观点进行列式解题。
类型二利用机械能守恒定律解决流体问题
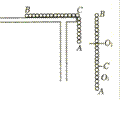
 [例2]如图所示,粗细均匀的U形管内装有总长为4L的水。开始时阀门K闭合,左右支管内水面高度差为L。打开阀门K后,左右水面刚好相平时左管液面的速度是多大?(管的内部横截面很小,摩擦阻力忽略不计)
[例2]如图所示,粗细均匀的U形管内装有总长为4L的水。开始时阀门K闭合,左右支管内水面高度差为L。打开阀门K后,左右水面刚好相平时左管液面的速度是多大?(管的内部横截面很小,摩擦阻力忽略不计)
导示:由于不考虑摩擦阻力,故整个水柱的机械能守恒。从初始状态到左右支管水面相平为止,相当于有长L/2的水柱由左管移到右管。系统的重力势能减少,动能增加。该过程中,整个水柱势能的减少量等效于高L/2的水柱降低L/2重力势能的减少。不妨设水柱总质量为8m,则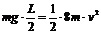 ,得
,得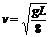 。
。
 本题在应用机械能守恒定律时仍然是用
本题在应用机械能守恒定律时仍然是用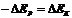 建立方程,在计算系统重力势能变化时用了等效方法。需要注意的是:研究对象仍然是整个水柱,到两个支管水面相平时,整个水柱中的每一小部分的速率都是相同的。
建立方程,在计算系统重力势能变化时用了等效方法。需要注意的是:研究对象仍然是整个水柱,到两个支管水面相平时,整个水柱中的每一小部分的速率都是相同的。
类型三用机械能守恒定律定律解决多体类
[例3](南京外国语学校高三年级第一次月考)一半径为R的半圆形竖直圆柱面,用轻质不可伸长的细绳连接的A、B两球,悬挂在圆柱面边缘两侧,A球质量为B球质量的2倍,现将A球从圆柱边缘处由静止释放,如图所示,已知A始终不离开球面,且细绳足够长,若不计一切摩擦.
 (1)求A球沿圆柱面滑至最
(1)求A球沿圆柱面滑至最
低点时速度的大小。
(2)求A球沿圆柱面运动的
最大位移。
导示:(1)设A球沿圆柱面滑至最低点时速
度的大小为v,则据机械能守恒定律可得:
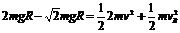
又因为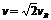
解得
(2)当A球的速度为0时,A球沿圆柱面运动的位移最大,设为s,则据机械能守恒
定律可得:
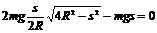
解得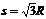


3.势能的相对性
2.势能属于系统所共有。重力势能是物体和地球组成的系统所共有的,而不是物体单独具有的,“物体的重力势能”只是一种简化的说法.同样弹性势能也是弹簧各部分组成的系统所共有。
1.重力势能会式中h表示物体相对于参考平面的高度,是个状态量。
2.机械能守恒定律
(1)内容:在只有重力(或弹簧的弹力)做功的情况下,物体的动能和重力势能(或弹性势能)发生相互转化,但机械能的总量保持不变,这个结论叫做机械能守恒定律。
(2)表达式:a.
b.
c.

知识点一势能的理解
1.机械能:动能和势能统称为机械能。
3.弹力做功与弹性势能变化的关系
弹性势能的改变量仅与弹力做功有关,弹力做多少正功,弹性势能就减少多少;弹力做多少负功,弹性势能就增加。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com