2．直线y=kx+3与x轴的交点是(1，0)，则k的值是(　 )

　　 A．3　　　 B．2　　　 C．-2　　　 D．-3

1．直线y=3x+9与x轴的交点是(　 )

　　 A．(0，-3)　　　 B．(-3，0)　　 C．(0，3)　　 D．(0，-3)

2．当自变量x为何值时，函数y=2x+20的值为0？

　　 这两个问题之间有什么联系吗？

　　 我们这节课就来研究这个问题，并学习利用这种关系解决相关问题的方法．

魔法师

　 　例：若直线y=kx+6与两坐标轴所围成的三角形面积是24，求常数k的值是多少？

　 　分析：(1)一次函数的图象与两条坐标轴围成的图形是直角三角形，两条直角边的长分别是图象与x轴的交点的横坐标的绝对值和与y轴的交点的纵坐标的绝对值．

　　 (2)确定图象与两条坐标轴的交点坐标可以通过令x=0和y=0解方程求得．

　 　解：设直线y=kx+6与x轴和y轴分别交于点A、B．

　　 令y=0得x=-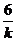；令x=0得y=6．

∴A(-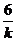，0)、B(0，6)　　

∴OA=|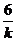|、OA=│6│=6　

∴S=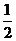OA·OB=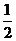|-|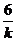×6=24

　　 ∴│k│= 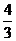　　∴k=±

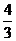
演兵场

　　 ☆我能选

1．解方程2x+20=0

2．应用函数求解一元一次方程．

学习难点

　　 用函数观点认识一元一次方程．

预习问题

我们来看下面两个问题：

1．函数观点认识一元一次方程．

2．在直角坐标系中，以方程kx-y+b=0的解为坐标的点组成的图象就是一次函数y=kx+b的图象．

学习重点

1．解关于x的方程kx+b=0可以转化为：已知函数y=kx+b的函数值为0，求相应的自变量的值．从图象上看，相当于已知直线y=kx+b，确定它与x轴的交点的横坐标．

14.3.1 一次函数与一元一次方程

学习目标

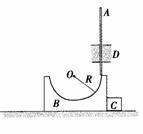
4．(南京市秦淮中学2007年物理高考模拟试卷)如图所示，B是质量为2m、半径为R的光滑半球形碗，放在光滑的水平桌面上。A是质量为m的细长直杆，光滑套管D被固定在竖直方向，A可以自由上下运动，物块C的质量为m，紧靠半球形碗放置。初始时，A杆被握住，使其下端正好与碗的半球面的上边缘接触(如图)。然后从静止开始释放A，A、B、C便开始运动。求：

(1)长直杆的下端运动到碗的最低点时，长直杆竖直方向的速度和B、C水平方向的速度；

　 (2)运动的过程中，长直杆的下端能上升到的最高点距离半球形碗底部的高度是多少?