
2. 静电场中的对称性
例2. (2005上海高考)如图1所示,带电量为+q的点电荷与均匀带电薄板相距为2d,点电荷到带电薄板的垂线通过板的几何中心。若图中b点处产生的电场强度为零,根据对称性,带电薄板在图中b点处产生的电场强度大小为多少,方向如何?(静电力恒量为k)。
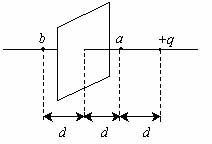
图1
解析:在电场中a点:
板上电荷在a、b两点的电场以带电薄板对称,带电薄板在b点产生的场强大小为,方向水平向左。
点评:题目中要求带电薄板产生的电场,根据中学物理知识仅能直接求点电荷产生的电场,无法直接求带电薄板产生的电场;由Ea=0,可以联想到求处于静电平衡状态的导体的感应电荷产生的场强的方法,利用来间接求出带电薄板在a点的场强,然后根据题意利用对称性求出答案。
例3. 静电透镜是利用静电场使电子束会聚或发散的一种装置,其中某部分静电场的分布如图2所示。虚线表示这个静电场在xOy平面内的一簇等势线,等势线形状相对于Ox轴、Oy轴对称,等势线的电势沿x轴正向增加,且相邻两等势线的电势差相等。一个电子经过P点(其横坐标为)时,速度与Ox轴平行。适当控制实验条件,使该电子通过电场区域时仅在Ox轴上方运动。在通过电场区域过程中,该电子沿y方向的分速度vy,随位置坐标x变化的示意图是:
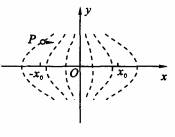
图2

解析:由于静电场的电场线与等势线垂直,且沿电场线电势依次降低,由此可判断Ox轴上方区域y轴左侧各点的场强方向斜向左上方,y轴右侧各点的场强方向斜向左下方。电子运动过程中,受到的电场力的水平分力沿x轴正方向,与初速方向相同,因此,电子在x方向上的分运动是加速运动,根据空间对称性,电子从x=运动到过程中,在y轴左侧运动时间比在y轴右侧运动的时间长。电子受到电场力的竖直分力先沿y轴负方向,后沿y轴正方向。因此电子在y方向上的分运动是先向下加速后向下减速,但由于时间的不对称性,减速时间比加速时间短,所以,当时,的方向应沿y轴负方向。正确答案为D。
1. 简谐运动中的对称性
例1. 劲度系数为k的轻质弹簧,下端挂一个质量为m的小球,小球静止时距地面的高度为h,用力向下拉球使球与地面接触,然后从静止释放小球(弹簧始终在弹性限度以内)则:
A. 运动过程中距地面的最大高度为2h
B. 球上升过程中势能不断变小
C. 球距地面高度为h时,速度最大
D. 球在运动中的最大加速度是kh/m
解析:因为球在竖直平面内做简谐运动,球从地面上由静止释放时,先做变加速运动,当离地面距离为h时合力为零,速度最大,然后向上做变减速运动,到达最高点时速度为零,最低点速度为零时距平衡位置为h,利用离平衡位置速度相同的两点位移具有对称性,最高点速度为零时距平衡位置也为h,所以球在运动过程中距地面的最大高度为2h,由于球的振幅为h,由可得,球在运动过程中的最大加速度为,球在上升过程中动能先增大后减小,由整个系统机械能守恒可知,系统的势能先减小后增大。所以正确选项为ACD。
22.(14分)
已知定义在R上的函数f(x)=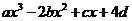 (a,b,c,d∈R)的图像关于原点对称,且x=1时,f(x)取得极小值
(a,b,c,d∈R)的图像关于原点对称,且x=1时,f(x)取得极小值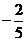 .
.
(1)求f(x)的解析式;
(2)当x∈[-1,1]时,函数图像上是否存在两点,使得过此两点处的切线互相垂直?证明你的结论;
(3)设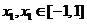 时,求证:|
时,求证:|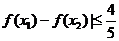 .
.
21.(12分)
在平面直角坐标系xoy中,点P到M(0,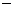
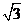 ),N(0,
),N(0,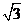 )的距离之和等于4,设点P的轨迹C.
)的距离之和等于4,设点P的轨迹C.
(1)写出曲线C的方程;
(2)设直线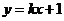 与曲线C交于A、B两点,k为何值时?
与曲线C交于A、B两点,k为何值时?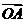
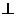
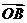 ,此时
,此时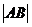 的值是多少?
的值是多少?
20.(12分)
已知数列{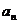 }的前n项和为
}的前n项和为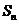 ,
,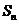 =
=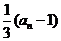
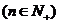 .
.
(1)求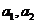 ;
;
(2)求数列{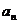 }的通项 .
}的通项 .
19.(12分)
如图,在正方体ABCD
-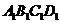 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面 的中心 .
的中心 .
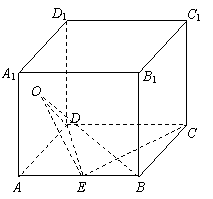 (1)求证:OB⊥EC ;
(1)求证:OB⊥EC ;
(2)求二面角O-DE-A的大小(用反三角函数表示).
]
18.(12分)
甲、乙围棋选手进行围棋比赛,采用五局三胜制(先胜三场者获胜).若每场比赛甲获胜的概率为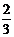 ,乙获胜的概率为
,乙获胜的概率为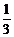 .求:
.求:
(1)甲以3∶0获胜的概率;
(2)甲获胜的概率.
17.(12分)求不等式的解集:
(1)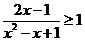 ;
;
(2)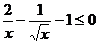 .
.
16.已知函数y= f(x)的图像的两个对称中心分别是M(2,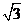 ),N (4,
),N (4,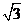 )且f(2)=2,
)且f(2)=2,
则f(6)= .
15.设f(x)=(1+2x)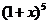 ,导函数f′(x)展开式中
,导函数f′(x)展开式中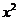 项的系数是 .
项的系数是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com