
6.线面平行与垂直的判定
(1)两直线平行的判定
①定义:在同一个平面内,且没有公共点的两条直线平行.
②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a?β,α∩β=b,则a∥b.
③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.
④两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b
(2)两直线垂直的判定
①定义:若两直线成90°角,则这两直线互相垂直.
②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c
③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b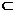 α,a⊥b.④三垂线定理和它的逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
α,a⊥b.④三垂线定理和它的逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
(3)直线与平面平行的判定
①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.
②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即
若a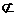 α,b
α,b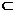 α,a∥b,则a∥α.
α,a∥b,则a∥α.
③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l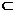 α,则l∥β.
α,则l∥β.
(4)直线与平面垂直的判定
①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m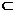 α,n
α,n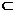 α,m∩n=B,l⊥m,l⊥n,则l⊥α.
α,m∩n=B,l⊥m,l⊥n,则l⊥α.
③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.
④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.
⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l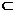 β,l⊥a,则l⊥α.
β,l⊥a,则l⊥α.
(5)两平面平行的判定
①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点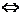 α∥β.
α∥β.
②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b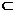 α,a∩b=P,a∥β,b∥β,则α∥β.
α,a∩b=P,a∥β,b∥β,则α∥β.
③垂直于同一直线的两平面平行.即若α⊥a,β⊥a,则α∥β.
④平行于同一平面的两平面平行.即若α∥β,β∥γ,则α∥γ.
(6)两平面垂直的判定
①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°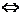 α⊥β.
α⊥β.
②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l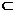 α,则α⊥β.
α,则α⊥β.
③一个平面垂直于两个平行平面中的一个,也垂直于另一个.即若α∥β,α⊥γ,则β⊥γ.
(7)线、线关系和线、面关系的辨证法


5.异面直线的判定
证明两条直线是异面直线通常采用反证法.
有时也可用“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.
4.空间线面的位置关系
 平行-没有公共点
平行-没有公共点
共面
(1)直线与直线 相交-有且只有一个公共点
异面(既不平行,又不相交)
 直线在平面内-有无数个公共点
直线在平面内-有无数个公共点
 (2)直线和平面 直线不在平面内 平行-没有公共点
(2)直线和平面 直线不在平面内 平行-没有公共点
(直线在平面外) 相交-有且只有一个公共点
 相交-有一条公共直线(无数个公共点)
相交-有一条公共直线(无数个公共点)
(3)平面与平面
平行-没有公共点
2.平面的基本性质
公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.
公理3 经过不在同一直线上的三个点,有且只有一个平面.
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
|
 3.证题方法
3.证题方法
|
|
 |
|||
|
|||
|
1、平面:几何里的平面是无限伸展的.平面通常用一个平行四边形来表示.
(1)平面的表示方法: 。
(2)用集合论中的符号表示它们之间的关系,例如:A∈l表示点A在直线l上;
A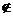 α表示点A不在平面α内;l
α表示点A不在平面α内;l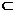 α表示直线l在平面α内;
α表示直线l在平面α内;
a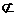 α表示直线a不在平面α内;l∩m=A表示直线l与直线m相交于A点;
α表示直线a不在平面α内;l∩m=A表示直线l与直线m相交于A点;
α∩l=A表示平面α与直线l交于A点;α∩β=l表示平面α与平面β相交于直线l.
18.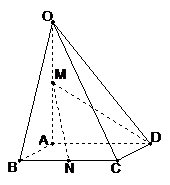 如图,在四棱锥
如图,在四棱锥 中,底面
中,底面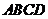 四边长为1的菱形,
四边长为1的菱形,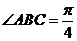 ,
, 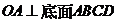 ,
, 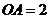 ,
,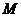 为
为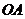 的中点,
的中点, 为
为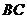 的中点
的中点
(Ⅰ)证明:直线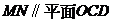
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
17. 如图,在四棱锥
如图,在四棱锥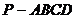 中,底面
中,底面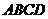 是矩形.已知
是矩形.已知 .
.
(Ⅰ)证明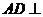 平面
平面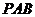 ;
;
(Ⅱ)求异面直线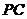 与
与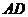 所成的角的大小;
所成的角的大小;
(Ⅲ)求点B到平面OCD的距离。
16.在体积为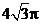 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC= ,A,C两点的球面距离为
,A,C两点的球面距离为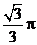 ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.
15.如图,已知球O点面上四点A、B、C、D,DA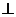 平面ABC,AB
平面ABC,AB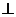 BC,DA=AB=BC=
BC,DA=AB=BC=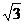 ,则球O点体积等于___________。
,则球O点体积等于___________。
14.若三棱锥的三个侧棱两两垂直,且侧棱长均为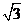 ,则其外接球的表面积是 .
,则其外接球的表面积是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com