1．速度选择器

正交的匀强磁场和匀强电场组成速度选择器。带电粒子必须以唯一确定的速度(包括大小、方向)才能匀速(或者说沿直线)通过速度选择器。否则将发生偏转。这个速度的大小可以由洛伦兹力和电场力的平衡得出：qvB=Eq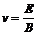，。在本图中，速度方向必须向右。

(1)这个结论与离子带何种电荷、电荷多少都无关。

(2)若速度小于这一速度，电场力将大于洛伦兹力，带电粒子向电场力方向偏转，电场力做正功，动能将增大，洛伦兹力也将增大，粒子的轨迹既不是抛物线，也不是圆，而是一条复杂曲线；若大于这一速度，将向洛伦兹力方向偏转，电场力将做负功，动能将减小，洛伦兹力也将减小，轨迹是一条复杂曲线。

[例题19]某带电粒子从图中速度选择器左端由中点O以速度v₀向右射去，从右端中心a下方的b点以速度v₁射出；若增大磁感应强度B，该粒子将打到a点上方的c点，且有ac=ab，则该粒子带___电；第二次射出时的速度为­_____。

解：B增大后向上偏，说明洛伦兹力向上，所以为带正电。由于洛伦兹力总不做功，所以两次都是只有电场力做功，第一次为正功，第二次为负功，但功的绝对值相同。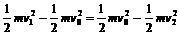，故。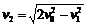

[例题20]如图所示，一个带电粒子两次以同样的垂直于场线的初速度v₀分别穿越匀强电场区和匀强磁场区， 场区的宽度均为L偏转角度均为α，求E∶B

解：分别利用带电粒子的偏角公式。在电场中偏转：

，在磁场中偏转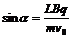：，由以上两式可得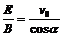。可以证明：当偏转角相同时，侧移必然不同(电场中侧移较大)；当侧移相同时，偏转角必然不同(磁场中偏转角较大)。

2．仔细审题，挖掘隐含条件。

[例题18]在 M、 N两条长直导线所在的平面内，一带电粒子的运动轨迹，如图所示．已知两条导线M、N只有一条中有恒定电流，另一条导线中无电流，关于电流、电流方向和粒子带电情况及运动方向，可能是

A．M中通有自上而下的恒定电流，带正电的粒子从b点向a点运动

B．M中通有自上而下的恒定电流，带负电的粒子从a点向b点运动

C．N中通有自下而上的恒定电流，带正电的粒子从b点向a点运动

D．N中通有自下而上的恒定电流，带负电的粒子从a点向b点运动

让学生讨论得出结果。很多学生会选择所有选项，或对称选择A、D(或B、C)。前者是因为没有考虑直线电流在周围产生非匀强磁场，带电粒子在其中不做匀速圆周运动。后者是在选择过程中有很强的猜测成分。

分析：两根直线电流在周围空间产生的磁场为非匀强磁场，靠近导线处磁场强，远离导线处磁场弱。所以带电粒子在该磁场中不做匀速圆周运动，而是复杂曲线运动。因为带电粒子在运动中始终只受到洛仑兹力作用，所以可以定性使用圆运动半径规律R=mv/ Bq。由该规律知，磁场越强处，曲率半径越小，曲线越弯曲；反之，曲线弯曲程度越小。

解：选项A、B正确。

小结：这是一道带电粒子在非匀强磁场中运动的问题，这时粒子做复杂曲线运动，不再是匀速圆周运动。但在定性解决这类问题时可使用前面所分析的半径公式。洛仑兹力永远不做功仍成立。

1．洛仑兹力永远不做功，因此磁场中带电粒子的动能不变。

3．画出轨迹草图并计算。

分析：带电粒子在两磁场中做半径不同的匀速圆周运动，但因为洛仑兹力永远不做功，所以带电粒子运动速率不变．粒子恰好不能通过两磁场的临界条件是粒子到达边界P时，其速度方向平行于边界面。粒子在磁场中轨迹如图所示。再利用平面几何和圆运动规律即可求解。

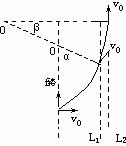解：如图所示，设O₁、O₂分别为带电粒子在磁场B₁和B₂中运动轨迹的圆心。则

在磁场B₁中运动的半径为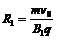

在磁场B₂中运动的半径为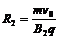

设角α、β分别为粒子在磁场B₁和B₂中运动轨迹所对应圆心角，则由几何关系知

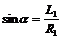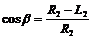，，且α+β＝90°

所以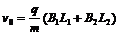

若粒子能通过两磁场区，则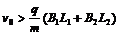

小结：

2．什么是粒子运动通过磁场或不通过磁场的临界条件？

1．该粒子在两磁场中运动速率是否相同？

3．讨论粒子速度方向发生变化后，粒子运动轨迹及速度偏转角的比。

分析：(1)圆运动半径可直接代入公式求解。

(2)先在圆中画出任意一速度方偏转角为初速度与未速度的夹角，且偏转角等于粒子运动轨迹所对应的圆心角。向入射时，其偏转角为哪个角？如图所示。由图分析知：弦ac是粒子轨迹上的弦，也是圆形磁场的弦。

因此，弦长的变化一定对应速度偏转角的变化，也一定对应粒子圆运动轨迹的圆心角的变化。所以当弦长为圆形磁场直径时，偏转角最大。

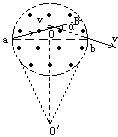解：(1)设粒子圆运动半径为R，则

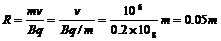
(2)由图知：弦长最大值为ab=2r=6×10^-2m

设速度偏转角最大值为α_m，此时初速度方向与ab连线夹角为θ，则

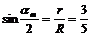，故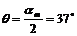

当粒子以与ab夹角为37°斜向右上方入射时，粒子飞离磁场时有最大偏转角，其最大值为74°。

小结：本题所涉及的问题是一个动态问题，即粒子虽然在磁场中均做同一半径的匀速圆周运动，但因其初速度方向变化，使得粒子运动轨迹的长短和位置均发生变化，要会灵活运用平面几何知识去解决．

计算机演示：(1)随粒子入射速度方向的变化，粒子飞离磁场时速度偏转角的变化。(2)随粒子入射速度方向的变化，粒子做匀速圆周运动的圆心的运动轨迹。其轨迹为以a点为圆心的一段圆弧。

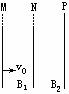[例题17]如图所示，很长的平行边界面M、N与N、P间距分别为L₁、L₂，其间分别有磁感应强度为B₁与B₂的匀强磁场区，磁场方向均垂直纸面向里．已知B₁≠B₂，一个带正电的粒子电量为q，质量为m，以大小为v₀。的速度垂直边界面M与磁场方向射入MN间磁场区，试讨论粒子速度v₀应满足什么条件，才能通过两个磁场区，并从边界面P射出？(不计粒子重力)

问题：

2．在图中画出粒子以图示速度方向入射时在磁场中运动的轨迹图，并找出速度的偏转角。

1．第一问由学生自己完成。

3．在xy平面内什么位置加一个圆形磁场可使带电质点按题意运动？其中有什么样特点的圆形磁场为半径最小的磁场？常见错误：

加以aM和bN连线交点为圆心的圆形磁场，其圆形磁场最小半径为R。

分析：带电质点在磁场中做匀速圆周运动，其半径为

因为带电质点在a、b两点速度方向垂直，所以带电质点在磁场中运动轨迹为1/4圆弧，O₁为其圆心，如图所示MN圆弧。

在xy平面内加以MN连线为弦，且包含MN圆弧的所有圆形磁场均可使带电质点完成题意运动。其中以MN连线为半径的磁场为最小圆形磁场。

解：设圆形磁场的圆心为O₂点，半径为r，则由图知：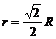

因为，所以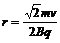

小结：这是一个需要逆向思维的问题，同时考查了空间想象能力，即已知粒子运动轨迹，求所加圆形磁场的位置。考虑问题时，要抓住粒子运动特点，即该粒子只在所加磁场中做匀速圆周运动，所以粒子运动的1/4圆弧必须包含在磁场区域中，且圆运动起点、终点必须是磁场边界上的点。然后再考虑磁场的最小半径。

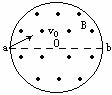
[例题16]在真空中，半径为r=3×10^-2m的圆形区域内，有一匀强磁场，磁场的磁感应强度为B=0.2T，方向如图所示，一带正电粒子，以初速度v₀=10⁶m/s的速度从磁场边界上直径ab一端a点处射入磁场，已知该粒子荷质比为q/m=10⁸C/kg，不计粒子重力，则(1)粒子在磁场中匀速圆周运动的半径是多少？(2)若要使粒子飞离磁场时有最大的偏转角，其入射时粒子的方向应如何(以v₀与Oa的夹角θ表示)？最大偏转角多大？

问题：