22．(10分)分析和解：(1)设电子经电压U₁加速后的速度为v₀，由动能定理

　　　 　　　　e U₁=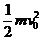－0…………………………………………(2分)

　　　　 解得　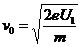 ………………………………..………(1分)

(2)电子以速度v₀进入偏转电场后，垂直于电场方向做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动。设偏转电场的电场强度为E，电子在偏转电场中运动的时间为t，加速度为a，电子离开偏转电场时的侧移量为y。由牛顿第二定律和运动学公式

　　　 　　　　　t=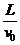……………………………………………..……….(1分)

F=ma　　 F=eE　 　E=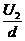

a =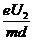……………………………………………(2分)

y=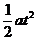……………………………………………(1分)

解得　 y=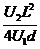…………………………………………(1分)

(3)减小加速电压U₁；增大偏转电压U₂；……

(本题的答案不唯一，只要措施合理，答出一项可得1分，答出两项及以上可得2分。)

22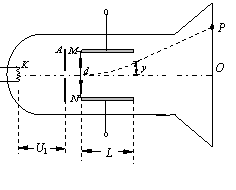．(10分)右下图为一真空示波管的示意图，电子从灯丝K发出(初速度可忽略不计)，经灯丝与A板间的电压U₁加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场)，电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点。 已知M、N两板间的电压为U₂，两板间的距离为d，板长为L，电子的质量为m，电荷量为e，不计电子受到的重力及它们之间的相互作用力。

(1)求电子穿过A板时速度的大小；

(2)求电子从偏转电场射出时的侧移量；

(3)若要使电子打在荧光屏上P点的上方，可采取哪些措施？

21．(10分)分析和解：(1)木块A在桌面上受到滑动摩擦力作用做匀减速运动，根据牛顿第二定律，木块A的加速度　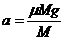　 ＝2.5m/s²………………………(1分)

设两木块碰撞前A的速度大小为v，根据运动学公式，得

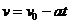＝2.0m/s……………………………(2分)

(2)两木块离开桌面后均做平抛运动，设木块B离开桌面时的速度大小为v₂，在空中飞行的时间为t′。根据平抛运动规律有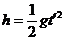：，s＝v₂t′…………………(2分)

解得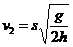：　　　　　　　　　　 ＝1.5m/s……………………………(1分)

(3)设两木块碰撞后木块A的速度大小为v₁，根据动量守恒定律有：

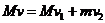…………………………………(1分)

解得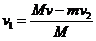：　　　　　　　　　　　 =0.80m/s…………………………(1分)

设木块A落到地面过程的水平位移为s′，根据平抛运动规律，得

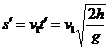　　　　　　　　　　　　　　 ＝0.32m………………………(1分)

则木块A落到地面上的位置与D点之间的距离　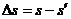 ＝0.28m ………(1分)

21．(10分)如图所示，在距水平地面高h＝0.80m的水平桌面一端的边缘放置一个质量m＝0.80kg的木块B，桌面的另一端有一块质量M=1.0kg的木块A以初速度v₀=4.0m/s开始向着木块B滑动，经过时间t=0.80s与B发生碰撞，碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点，它们的碰撞时间极短，且已知D点距桌面边缘的水平距离s=0.60m，木块A与桌面间的动摩擦因数μ=0.25，重力加速度取g＝10m/s²。求：

(1)两木块碰撞前瞬间，木块A的速度大小；

(2)木块B离开桌面时的速度大小；

(3)木块A落到地面上的位置与D点之间的距离。

20.(8分)分析和解：(1)带电粒子经过电场加速，进入偏转磁场时速度为v，由动能定理

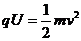　 　　…………………①(1分)

进入磁场后带电粒子做匀速圆周运动，轨道半径为r

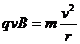………………②(2分)

　 打到H点有　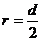　………………………③(1分)

由①②③得　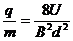…………(1分)

(2)要保证所有带电粒子都不能打到MN边界上，带电粒子在磁场中运动偏角小于90°，临界状态为90°，如图所示，磁场区半径

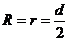　　　　　　　(2分)

　所以磁场区域半径满足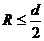　　(1分)

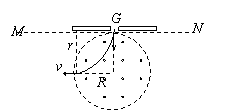
20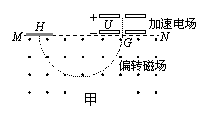．(8分)在甲图中，带正电粒子从静止开始经过电势差为U的电场加速后，从G点垂直于MN进入偏转磁场。该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场，磁场的磁感应强度为B，带电粒子经偏转磁场后，最终到达照相底片上的H点．测得G、H间的距离为 d，粒子的重力可忽略不计。

(1)设粒子的电荷量为q，质量为m，试证明该粒子的比荷为：；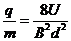

(2)若偏转磁场的区域为圆形，且与MN相切于G点，如图乙所示，其它条件不变。要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长)，求磁场区域的半径应满足的条件。

19.(8分)分析和解：(1)导体棒、金属导轨和直流电源构成闭合电路，根据闭合电路欧姆定律有：

I=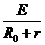=1.5A…………(3分)

(2)导体棒受到的安培力：

F_安=BIL=0.30N…………(2分)

(3)导体棒所受重力沿斜面向下的分力F₁= mg sin37º=0.24N

由于F₁小于安培力，故导体棒受沿斜面向下的摩擦力f…………(1分)

　　 根据共点力平衡条件

　　　 mg sin37º+f=F_安…………(1分)

解得：f=0.06N …………(1分)

19．(8分)如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37º，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场。金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源。现把一个质量m=0.040kg的导体棒ab放在金属导轨上，导体棒恰好静止。导体棒与金属导轨垂直、且接触良好，导体棒与金属导轨接触的两点间的电阻R₀=2.5Ω，金属导轨电阻不计，g取10m/s²。已知sin37º=0.60，cos37º=0.80，求：

(1)通过导体棒的电流；

(2)导体棒受到的安培力大小；

(3)导体棒受到的摩擦力大小。

18．(8分)分析和解：

(1)　　　　 因为金属块匀速运动，所以

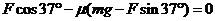　　 _{………………}(2分)

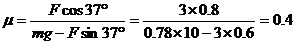_{…………(2分)}

(2)撤去拉力后a=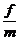=μg _{………　 (1分)}

=4m/s² _{………(1分)}

金属块在桌面上滑行的最大距离s = 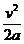　_{………(1分)}

=

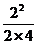
=0.5m_{……………… (1分)}

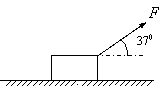
18．(8分)如图所示，质量为0.78kg的金属块放在水平桌面上，在与水平方向成37°角斜向上、大小为3.0N的拉力F作用下，以2.0m／s的速度向右做匀速直线运动．(sin37°=0.60，cos37°＝0.80，g取10m/s²)求：

(1)金属块与桌面间的动摩擦因数；

(2)如果从某时刻起撤去拉力，撤去拉力后金属块在桌面上滑行的最大距离。