1．(崇文区)如图所示，两个物体A和B，质量分别为M和m，用跨过定滑轮的轻绳相连，A静止于水平地面上，不计摩擦，则下列说法正确的是　　　　　　　　　　 (　　　 )

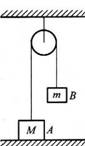A．物体A对绳的作用力大小为Mg

B．物体A对绳的作用力大小为mg

C．物体A对地面的作用力大小为Mg

D．物体A对地面的作用力大小为(M+m) g

5.

(1)金属棒MN沿导轨竖直向上运动，进入磁场中切割磁感线产生感应电动势。当金属棒MN匀速运动到C点时，电路中感应电动势最大，产生的感应电流最大。

金属棒MN接入电路的有效长度为导轨OCA形状满足的曲线方程中的x值。因此接入电路的金属棒的有效长度为

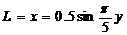　 　　L_m=x_m=0.5m

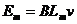　　　 E_m=3.0V

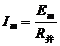　　　 且　　　　　　

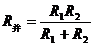
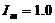A

(2)金属棒MN匀速运动中受重力mg、安培力F_安、外力F_外作用

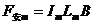
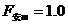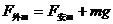
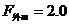N

N

(3)金属棒MN在运动过程中，产生的感应电动势

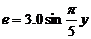
有效值为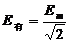　

金属棒MN滑过导轨OC段的时间为t

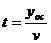
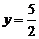　　　 m

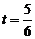s　

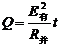
滑过OC段产生的热量　 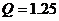　　J.

4.

分析和解：(1)导体棒、金属导轨和直流电源构成闭合电路，根据闭合电路欧姆定律有：

I=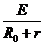=1.5A…………(3分)

(2)导体棒受到的安培力：

F_安=BIL=0.30N…………(2分)

(3)导体棒所受重力沿斜面向下的分力F₁= mg sin37º=0.24N

由于F₁小于安培力，故导体棒受沿斜面向下的摩擦力f…………(1分)

　　 根据共点力平衡条件

　　　 mg sin37º+f=F_安…………(1分)

解得：f=0.06N …………(1分)

3．

解：

(1)感应电动势为 E=BLv=1.0V

感应电流为　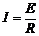 =1.0 A　　　　　　　　　　　　　　　　　　 (4分)

(2)导体棒匀速运动，安培力与拉力平衡

即有F=BIL=0.1N 　　　　　　　　　　　　　　　　　　　　　　(4分)

(3) 导体棒移动30cm的时间为　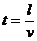 = 0.03s　　　　　　　　

根据焦耳定律， Q₁ = I²R t = 0.03J　 (或Q₁=Fs=0.03J)

根据能量守恒， Q₂=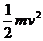= 0.5J

电阻R上产生的热量　 Q = Q₁+Q₂ = 0.53J　　　　　　　　　　　 (4分)

2．

解：(1)由楞次定律(或右手定则)，线框中感应电流的方向为逆时针(或abcda)…………(2分)

(2)设t=2.0s时的速度为v，据题意有：BLv=IR 解得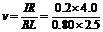m/s=0.4m/s………(3分)

(3)设t=5.0s时的速度为v′,整个过程中线框中产生的焦耳热为Q，则有：

BLv′=I′R………………………………(1分)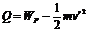，　 …………………………(2分)

由上述两式解得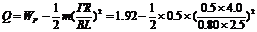：J=1.67J……………(1分)

1．

解：(1)根据法拉第电磁感应定律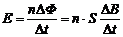　　 (3分)　

　　 求出　　　　 E = 1.2(V)　　　　　　　　　 (1分)

(2)根据全电路欧姆定律 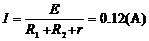　(1分)

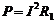　　　　 根据　　　　 　　　　　　　　　　　　(1分)

　　 求出　　　 　P = 5.76×10^-2(W)　　　 　　　　(1分)

(3)S断开后，流经R₂的电量即为S闭合时C板上所带的电量Q

电容器两端的电压　　 U = IR₂＝0.6(V)　　 (1分)

流经R₂的电量　　 Q = CU = 1.8×10^-5(C)　　 (2分)

1　 AC

1. (1)a=5m/s² 向下；(2)v₀=5m/s　　　　　

9.　 BC

1　 AD　　

2　 BCD　　

3　 ABD

4　 AD　　

5　 BCD　

6　 BCD　

7　 BD

8.　 BCD