
3.
解:(1)由楞次定律(或右手定则),线框中感应电流的方向为逆时针(或abcda)…………(2分)
(2)设t=2.0s时的速度为v,据题意有:BLv=IR 解得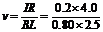 m/s=0.4m/s………(3分)
m/s=0.4m/s………(3分)
(3)设t=5.0s时的速度为v′,整个过程中线框中产生的焦耳热为Q,则有:
BLv′=I′R………………………………(1分), 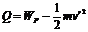 …………………………(2分)
…………………………(2分)
由上述两式解得: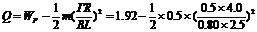 J=1.67J……………………(1分)
J=1.67J……………………(1分)
4?
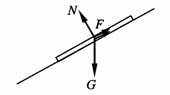 (1)(共4分)线框在磁场区域做匀速运动时,其受力如图所示:
(1)(共4分)线框在磁场区域做匀速运动时,其受力如图所示:
∴ F=mgsinθ
又安培力: F=BIl (1分)
感应电流: I=E/R
感应电动势: E=Blv (1分)
解得匀速运动的速度: v=mgRsinθ/B2l2(2分)
(2)(共2分)在进入磁场前,线框的加速度a=gsinθ (1分)
所以线框进入磁场前下滑的距离s=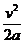 =
=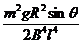 (1分)
(1分)
(3)(共2分)过程中线框沿斜面通过了2 l的距离,所以:Q热=mg·2lsinθ
2.
解:
(1)感应电动势为 E=BLv=1.0V
感应电流为 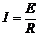 =1.0 A
(4分)
=1.0 A
(4分)
(2)导体棒匀速运动,安培力与拉力平衡
即有F=BIL=0.1N (4分)
(3) 导体棒移动30cm的时间为 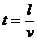 = 0.03s
= 0.03s
根据焦耳定律, Q1 = I2R t = 0.03J (或Q1=Fs=0.03J)
根据能量守恒, Q2=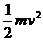 = 0.5J
= 0.5J
电阻R上产生的热量 Q = Q1+Q2 = 0.53J (4分)
1.
(1)金属棒MN沿导轨竖直向上运动,进入磁场中切割磁感线产生感应电动势。当金属棒MN匀速运动到C点时,电路中感应电动势最大,产生的感应电流最大。
金属棒MN接入电路的有效长度为导轨OCA形状满足的曲线方程中的x值。因此接入电路的金属棒的有效长度为
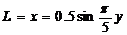 Lm=xm=0.5m
Lm=xm=0.5m
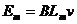 Em=3.0V
Em=3.0V
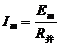 且
且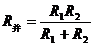
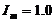 A
A
(2)金属棒MN匀速运动中受重力mg、安培力F安、外力F外作用
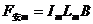
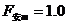 N
N
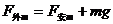
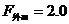 N
N
(3)金属棒MN在运动过程中,产生的感应电动势
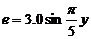
有效值为 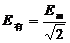
金属棒MN滑过导轨OC段的时间为t
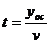
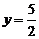 m
m
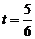 s
s
滑过OC段产生的热量 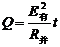
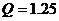 J
J
1. BDF ; 偏小; g=4π2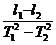
1. AD 2. BC 3. ABD 4. AD
6. C 7. D 8. C 9. C 10. C
1. B 2. B 3. B 4. D 5. A
4.(宣武区)用质量为m、总电阻为R的导线做成边长为l的正方形线框MNPQ,并将其放在倾角为θ的平行绝缘导轨上,平行导轨的间距也为l,如图所示。线框与导轨之间是光滑的,在导轨的下端有一宽度为l(即ab=l)、磁感应强度为B的有界匀强磁场,磁场的边界aa′、bb′垂直于导轨,磁场的方向与线框平面垂直。
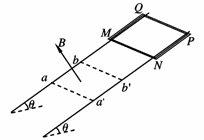 某一次,把线框从静止状态释放,线框恰好能够匀速地穿过磁场区域。若当地的重力加速度为g,求:
某一次,把线框从静止状态释放,线框恰好能够匀速地穿过磁场区域。若当地的重力加速度为g,求:
(1)线框通过磁场时的运动速度;
(2)开始释放时,MN与bb′之间的距离;
(3)线框在通过磁场的过程中所生的热。
北京市各区2009年高三上学期期末试题分类精编
振动、波和热学
3.(西城区)如图(甲)所示,边长为L=2.5m、质量m=0.50kg的正方形绝缘金属线框,平放在光滑的水平桌面上,磁感应强度B=0.80T的匀强磁场方向竖直向上,金属线框的一边ab与磁场的边界MN重合.在力F作用下金属线框由静止开始向左运动,在5.0s内从磁场中拉出.测得金属线框中的电流随时间变化的图象如图(乙)所示.已知金属线框的总电阻为R=4.0Ω.
(1)试判断金属线框从磁场中拉出的过程中,线框中的感应电流方向?
(2)t=2.0s时,金属线框的速度?
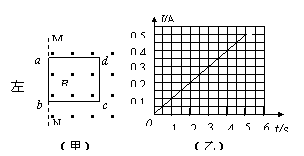 (3)已知在5.0s内力F做功1.92J,那么,金属框从磁场拉出过程线框中产生的焦耳热是多少?
(3)已知在5.0s内力F做功1.92J,那么,金属框从磁场拉出过程线框中产生的焦耳热是多少?
2.(丰台区)如图所示,宽度为L=0.20 m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=1.0Ω的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B=0.50 T。一根质量为m=10g的导体棒MN放在导轨上与导轨接触良好,导轨和导体棒的电阻均可忽略不计。现用一平行于导轨的拉力拉动导体棒沿导轨向右匀速运动,运动速度v=10 m/s,在运动过程中保持导体棒与导轨垂直。求:
(1)在闭合回路中产生的感应电流的大小;
(2)作用在导体棒上的拉力的大小;
(3)当导体棒移动30cm时撤去拉力,求整个过程中电阻R上产生的热量。
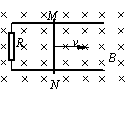
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com