
7] 1 3 12 8 4 9 10
[7 1] 3 12 8 4 9 10
[7 3 1] 12 8 4 9 10
[12 7 3 1] 8 4 9 10
[12 8 7 3 1] 4 9 10
[12 8 7 4 3 1] 9 10
[12 9 8 7 4 3 1] 10
[12 10 9 8 7 4 3 1]
冒泡排序
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
1 |
1 |
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
||
|
3 |
3 |
1 |
|
12 |
|
12 |
|
12 |
|
12 |
|
12 |
||
|
12 |
12 |
12 |
|
1 |
|
8 |
|
8 |
|
8 |
|
8 |
||
|
8 |
8 |
8 |
|
8 |
|
1 |
|
4 |
|
4 |
|
4 |
||
|
4 |
4 |
4 |
|
4 |
|
4 |
|
1 |
|
9 |
|
9 |
||
|
9 |
9 |
9 |
|
9 |
|
9 |
|
9 |
|
1 |
|
10 |
||
|
10 |
10 |
10 |
|
10 |
|
10 |
|
10 |
|
10 |
|
|
第一趟
|
7 |
|
7 |
|
12 |
|
12 |
|
12 |
|
12 |
|
3 |
|
12 |
|
8 |
|
8 |
|
9 |
|
10 |
|
12 |
|
8 |
|
7 |
|
9 |
|
10 |
|
9 |
|
8 |
|
4 |
|
9 |
|
10 |
|
8 |
|
8 |
|
4 |
|
9 |
|
10 |
|
7 |
|
7 |
|
7 |
|
9 |
|
10 |
|
4 |
|
4 |
|
4 |
|
4 |
|
10 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
第2趟 第3趟 第4趟 第5趟 第6趟
点评:直接插入法和冒泡法排序是常见的排序方法,通过该例,我们对比可以发现,直接插入排序比冒泡排序更有效一些,执行的操作步骤更少一些.
例6.给出以下四个数:6,-3,0,15,用直接插入法排序将它们按从小到大的顺序排列,用冒泡法将它们按从大到小的顺序排列.
分析:不论从大到小的顺序还是按从大到小的顺序,都可按两种方法的步骤进行排序。
解析:
直接插入排序法:
题型1:求最大公约数
例1.(1)用辗转相除法求123和48的最大公约数?
(2)用更相减损来求80和36的最大公约数?
解析:(1)辗转相除法求最大公约数的过程如下:(建立带余除式)
123=2×48+27 
48=1×27+21
27=1×21+6
21=3×6+3
6=2×3+0
最后6能被3整除,得123和48的最大公约数为3。
(2)分析:我们将80作为大数,36作为小数,执行更相减损术来求两数的最大公约数。执行结束的准则是减数和差相等.
更相减损术:
因为80和36都是偶数,要去公因数2。
80÷2=40,36÷2=18;
40和18都是偶数,要去公因数2。
40÷2=20,18÷2=9
下面来求20与9的最大公约数,
20-9=11
11-9=2
9-2=7
7-2=5
5-2=3
3-2=1
2-1=1
可得80和36的最大公约数为22×1=4。
点评:对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等。
例2.设计一个算法,求出840与1764的最大公因数。
解析:我们已经学习过了对自然数的素因数分解的方法,下面的算法就是在此基础上设计的。
解题思路如下:
首先对两个数进行素因数分解:
840=23×3×5×7,1764=22×32×72,
其次,确定两个数的公共素因数:2,3,7。
接着确定公共素因数的指数:对于公共素因数2,840中为23,1764中为22,应取较少的一个22,同理可得下面的因数为3和7。
算法步骤:
第一步:将840进行素数分解23×3×5×7;
第二步:将1764进行素数分解22×32×72;
第三步:确定它们的公共素因数:2,3,7;
第四步:确定公共素因数2,3,7的指数分别是:2,1,1;
第五步:最大公因数为22×31×71=84。
点评:质数是除1以外只能被1和本身整除的正整数,它应该是无限多个,但是目前没有一个规律来确定所有的质数.
题型2:秦九韶算法
例3.(2009福州模拟)如果执行右面的程序框图,那么输出的 ( )
( )
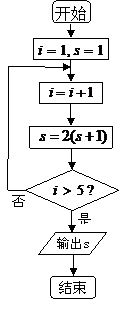
A.22 B.46 C.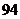 D.190
D.190
答案 C
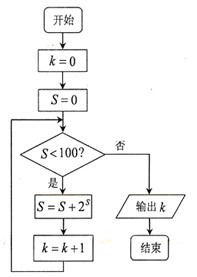
2、(2009浙江卷理)某程序框图如图所示,该程序运行后输出的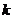 的值是 ( )
的值是 ( )
A.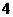 B.
B.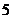 C.
C.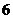 D.
D.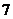
[解析]对于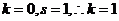 ,而对于
,而对于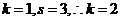 ,则
,则
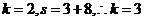 ,后面是
,后面是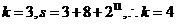 ,不
,不
符合条件时输出的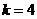 .
.
答案 A
4.进位制
(1)概念
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制。现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
对于任何一个数,我们可以用不同的进位制来表示。比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的。
一般地,若k是一个大于一的整数,那么以k为基数的k进制可以表示为:
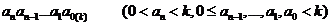 ,
,
而表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数。
(2)进位制间的转换
关于进位制的转换,教科书上以十进制和二进制之间的转换为例讲解,并推广到十进制和其它进制之间的转换。这样做的原因是,计算机是以二进制的形式进行存储和计算数据的,而一般我们传输给计算机的数据是十进制数据,因此计算机必须先将十进制数转换为二进制数,再处理,显然运算后首次得到的结果为二进制数,同时计算机又把运算结果由二进制数转换成十进制数输出。
非十进制数转换为十进制数比较简单,只要计算下面的式子值即可:
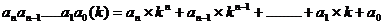

第一步:从左到右依次取出k进制数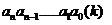 各位上的数字,乘以相应的k的幂,k的幂从n开始取值,每次递减1,递减到0,即
各位上的数字,乘以相应的k的幂,k的幂从n开始取值,每次递减1,递减到0,即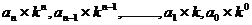 ;
;
第二步:把所得到的乘积加起来,所得的结果就是相应的十进制数。
十进制数转换成非十进制数
把十进制数转换为二进制数,教科书上提供了“除2取余法”,我们可以类比得到十进制数转换成k进制数的算法“除k取余法”。
非十进制之间的转换
一个自然的想法是利用十进制作为桥梁。教科书上提供了一个二进制数据与16进制数据之间的互化的方法,也就是先有二进制数转化为十进制数,再由十进制数转化成为16进制数。
7.将新数据列中的第7个数97与右边相邻的数49进行比较,因为49<97,97应下沉,所以顺序改变,得到新的数据列:
{38,49,65, 76, 13,97, 49,27}
我们把上述过程称为一趟排序。其基本特征是最大的数据沉到底,即排在最左边位置上的数据是数组中最大的数据。反复执行上面的步骤,就能完成排序工作,排序过程不会超过7趟。这种排序的方法称为冒泡排序。
上面的分析具有一般性,如果数据列有n个数据组成,至多经过n-1趟排序,就能完成整个排序过程.
6.将新数据列中的第6个数97与右边相邻的数27进行比较,因为27<97,97应下沉,所以顺序改变,得到新的数据列:
{38,49,65, 76, 13,97,27,49}
5.将新数据列中的第5个数97与右边相邻的数13进行比较,因为13<97,97应下沉,所以顺序改变,得到新的数据列:
{38,49,65, 76, 13,97,27,49}
4.将新数据列中的第4个数97与右边相邻的数76进行比较,因为76<97,97应下沉,所以顺序不变,得到新的数据列:
{38,49,65, 76,97,13,27,49}
3.将新数据列中的第3个数65与右边相邻的数97进行比较,因为97>65,所以顺序不变,得到新的数据列:
{38,49,65,97,76,13,27,49}
2.将新数据列中的第2个数49与右边相邻的数65进行比较,因为65>49,所以顺序不变,得到新的数据列:
{38,49,65,97,76,13,27,49}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com