
6.直线y=-3x-3与x轴的交点坐标是________,则不等式-3x+9>12的解集是________.
5.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是________.
4.当自变量x的值满足____________时,直线y=-x+2上的点在x轴下方.
3.已知关于x的不等式ax+1>0(a≠0)的解集是x<1,则直线y=ax+1与x轴的交点是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
☆我能填
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于x的不等式2x+k<0的解集是( )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
1.直线y=x-1上的点在x轴上方时对应的自变量的范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2.当自变量x为何值时函数y=2x-4的值大于0?
在问题1中,不等式5x+6>3x+10可以转化为2x-4>0,解这个不等式得x>2.
解问题2就是要解不等式2x-4>0,得出x>2时函数y=2x-4的值大于0.因此这两个问题实际上是同一个问题.
那么,是不是所有的一元一次不等式都可转化为一次函数的相关问题呢?它在函数图象上的表现是什么?如何通过函数图象来求解一元一次不等式?
以上这些问题,我们本节将要学到,请你认真预习一下吧.
魔法师
例:用画图象的方法解不等式2x+1>3x+4
分析:(1)可将不等式化为-x-3>0,作出直线y=-x-3,然后观察:自变量x取何值时,图象上的点在x轴上方?
或(2)画出直线y=2x+1与y=3x+4,然后观察:对于哪些x的值,直线y=2x+1上的点在直线y=3x+4上相应的点的上方?
解:方法(1)原不等式为:-x-3>0,在直角坐标系中画出函数y=-x-3的图象(图1).从图象可以看出,当x<-3时这条直线上的点在x轴上方,即这时y=-x-3>0,因此不等式的解集是x<-3.
方法(2) 把原不等式的两边看着是两个一次函数,在同一坐标系中画出直线y=2x+1与y=3x+4(图2),从图象上可以看出它们的交点的横坐标是x=-3,因此当x<-3时,对于同一个x的值,直线y=2x+1上的点在直线y=3x+4上相应点的上方,此时有2x+1>3x+4,因此不等式的解集是x<-3.
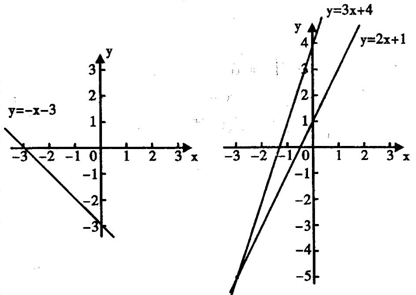
(1) (2)
演兵场
☆我能选
1.解不等式5x+6>3x+10.
2.掌握用图象求解不等式的方法.
学习难点
图象法求解不等式中自变量取值范围的确定.
预习问题
我们来看下面两个问题有什么关系?
1.理解一元一次不等式与一次函数的转化关系及本质联系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com