当外界条件(恒温恒容或恒温恒压)一定时, 同一可逆反应无论从正反应开始还是从逆反应开始,平衡时平衡混合物中任何相同组分的分数(体积、物质的量)均相等，这样的化学平衡互称为等效平衡。

15．(2008·江苏)已知函数f₁(x)＝3|x－p₁|，f₂(x)＝2·3|x－p₂|(x∈R，p₁，p₂为常数)，函数f(x)定义为：对每个给定的实数x，f(x)＝

(1)求f(x)＝f₁(x)对所有实数x成立的充分必要条件(用p₁，p₂表示)；

(2)设a，b是两个实数，满足a<b，且p₁，p₂∈(a，b)．若f(a)＝f(b)，求证：函数f(x)在区间[a，b]上的单调增区间的长度之和为(闭区间[m，n]的长度定义为n－m)．

解：(1)由f(x)的定义可知，

f(x)＝f₁(x)(对所有实数x)

等价于f₁(x)≤f₂(x)(对所有实数x)，

这又等价于3|x－p₁|≤2·3|x－p₂|，

即3|x－p₁|－|x－p₂|≤2对所有实数x均成立．(*)

易知函数|x－p₁|－|x－p₂|(x∈R)的最大值为|p₂－p₁|，故(*)等价于3|p₂－p₁|≤2，即|p₂－p₁|≤log₃2，这就是所求的充分必要条件．

(2)分两种情形讨论．

(ⅰ)当|p₁－p₂|≤log₃2时，由(1)知f(x)＝f₁(x)(对所有实数x∈[a，b])，则由f(a)＝f(b)及a<p₁<b易知p₁＝.再由f₁(x)＝的单调性可知，f(x)在区间[a，b]上的单调增区间的长度为b－＝.如下图．

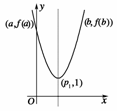
(ⅱ)当|p₁-p₂|>log₃2时，

不妨设p₁<p₂，则p₂-p₁>log₃2.

于是，当x≤p₁时，

有f₁(x)=3p₁-x<3p₂-x<f₂(x)，

从而f(x)=f₁(x)．

当x≥p₂时，f₁(x)=3x-p₁=3p₂-p₁·3x-p₂>3log₃2·3x-p₂=f₂(x)，从而f(x)=f₂(x)．

当p₁<x<p₂时，f₁(x)=3x-p₁及f₂(x)=2·3p₂-x.

由方程3^x₀-p₁=2·3^p2-x0，解得f₁(x)与f2(x)图象交点的横坐标为

显然p₁<x₀＝P₂－[(p₂－p₁)－log₃2]<p₂，这表明x₀在p₁与p₂之间．

由①易知f(x)＝

综上可知，在区间[a，b]上，

f(x)＝

如下图所示．

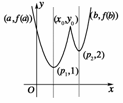
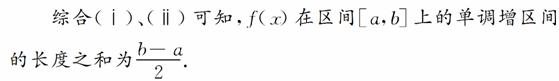
14．已知函数f(x)＝lg(k∈R且k>0)．

(1)求函数f(x)的定义域；

(2)若函数f(x)在[10，+∞)上单调递增，求k的取值范围．

解：(1)由>0及k>0得：>0.

①当0<k<1时，得x<1或x>；

②当k＝1时，得>0，∴x∈R且x≠1

③当k>1时，得x<或x>1，即x∈∪(1，+∞)；

综上，所求函数的定义域：当0<k<1时为(－∞，1)∪；当k>1时为∪(1，+∞)；当k＝1时为{x|x∈R且x≠1}．

(2)由f(x)在[10，+∞)上是增函数，∴>0得k>.

又f(x)＝lg＝lg，对任意的x₁、x₂，当10≤x₁<x₂时，有f(x₁)<f(x₂)，即lg<lg，

得：<⇔(k－1)<0，

又∵>，

∴k－1<0，∴k<1.

综上可知k的取值范围是.

13．(2009·安徽安庆质检)函数f(x)＝log₂的定义域为集合A，关于x的不等式2^2ax<()^a+2x(a∈R)的解集为B，求使A∪B＝B的实数a的取值范围．

解：∵A∪B＝B，∴A⊂B.

由>0⇒A＝{x|1<x<2}；

由2^2ax<()^a+2x⇒2ax<－a－2x，即2(a+1)x<－a，

①若a+1<0即a<－1，

则x>－.∵A⊂B，

∴－≤1⇒a≤－.∴a<－1.

②若a+1＝0即a＝－1，则x∈R，满足A⊂B，

∴a＝－1适合；

③若a+1>0，即a>－1，则x<－，

∵A⊂B，

∴－≥2⇒a≤－⇒－1<a≤－.

综上，a∈(－∞，－]．

12．定义在R上的奇函数f(x)有最小正周期为2，且x∈(0,1)时，f(x)＝.

(1)求f(x)在[－1,1]上的解析式；

(2)判断f(x)在(0,1)上的单调性；

(3)当λ为何值时，方程f(x)＝λ在x∈[－1,1]上有实数解．

解：(1)∵f(x)是x∈R上的奇函数，

∴f(0)＝0.

又∵2为最小正周期，

∴f(1)＝f(1－2)＝f(－1)＝－f(1)＝0.

设x∈(－1,0)，则－x∈(0,1)，

f(－x)＝＝＝－f(x)，

∴f(x)＝－，

∴f(x)＝

(2)设0<x₁<x₂<1，

f(x₁)－f(x₂)

＝

＝>0，

∴f(x)在(0,1)上为减函数．

(3)∵f(x)在(0,1)上为减函数，

∴<f(x)<，

即f(x)∈(，)．

同理，x在(－1,0)上时，f(x)∈(－，－)．

又f(－1)＝f(0)＝f(1)＝0，

∴当λ∈(－，－)∪(，)或λ＝0时，f(x)＝λ在[－1,1]内有实数解．

11．(2007·山东)函数y＝log_a(x+3)－1(a>0，a≠1)的图象恒过定点A，若点A在直线mx+ny+1＝0上，其中mn>0，则+的最小值为__________．

答案：8

解析：∵y＝log_a(x+3)－1，恒过点(－2，－1)，

∴A(－2，－1)，又A在直线上，

∴－2m－n+1＝0.即2m+n＝1.

又mn>0，∴m>0，n>0.

而+＝+

＝2++2+≥4+2＝8.

当n＝，m＝取“＝”，

∴+的最小值为8.故填8.

10．(2009·成都市外国语学校)已知函数f(x)＝2^x－1的反函数为f^－1(x)，g(x)＝log₄(3x+1)，若f^－1(x)≤g(x)，则x的取值范围是________．

答案：[0,1]

解析：由y＝2^x－1得y∈(－1，+∞)，∵y+1＝2^x，∴x＝log₂(y+1)，∴f^－1(x)＝log₂(x+1)(x∈(－1，+∞))．

∵f^－1(x)≤g(x)，∴log₂(x+1)≤log₂，∴0<x+1≤，解得0≤x≤1.

9．(2009·成都市一诊测)设函数f(x)＝e^2(x－1)，y＝f^－1(x)为y＝f(x)的反函数，若函数g(x)＝，则g[g(－1)]＝________.

答案：1

解析：依题意得g(－1)＝－1+2＝1，g[g(－1)]＝g(1)＝f^－1(1)．设f^－1(1)＝t，则有f(t)＝1，即e^2(t－1)＝1，t＝1，所以g[g(－1)]＝1.

8．(2009·保定市调研)若函数f(x)＝log₂的定义域和值域均为[1，+∞)，则实数a的取值集合为(　)

A．{0} 　　　　　　　　　　　　　　　　　　　　　　　 B．{a|0≤a≤1}

C．{a|a≥0}　 　　　　　　　　　　　　　　　　　　 D．{a|a≥2}

答案：A

解析：由题意得，log₂≥1在x≥1时恒成立，即≥2在x≥1时恒成立；

而≥2即x++a≥2，函数g(x)＝x++a在[1，+∞)上为增函数；

∴g(x)≥g(1)＝1+1+a≥2恒成立，∴a≥0.

由g(x)在[1，+∞)上为增函数，可知f(x)在[1，+∞)也为增函数，∴f(1)＝1，∴a＝0，选A.

7．设函数f(x)＝若f(x₀)>1，则x₀的取值范围是(　)

A．(－∞，0)∪(2，+∞)　 　　　　　　　 B．(0,2)

C．(－∞，－1)∪(3，+∞)　 　　　　　 D．(－1,3)

答案：C

解析：当x₀∈[2，+∞)时，由f(x₀)＝log₂(x₀－1)>1，得x₀>3；

当x₀∈(－∞，2)时，由f(x₀)＝()x₀－1>1，得x₀<－1.所以x₀∈(－∞，－1)∪(3，+∞)．故选C.