
6.直线与圆锥曲线的位置关系:
(1)相交: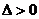
 直线与椭圆相交;
直线与椭圆相交;  直线与双曲线相交,但直线与双曲线相交不一定有
直线与双曲线相交,但直线与双曲线相交不一定有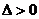 ,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故
,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故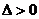 是直线与双曲线相交的充分条件,但不是必要条件;
是直线与双曲线相交的充分条件,但不是必要条件; 直线与抛物线相交,但直线与抛物线相交不一定有
直线与抛物线相交,但直线与抛物线相交不一定有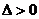 ,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故
,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故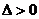 也仅是直线与抛物线相交的充分条件,但不是必要条件。
也仅是直线与抛物线相交的充分条件,但不是必要条件。
如(1)若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点,则k的取值范围是_______;
(2)直线y―kx―1=0与椭圆 恒有公共点,则m的取值范围是_______
恒有公共点,则m的取值范围是_______
(3)过双曲线 的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条
的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条
(2)相切:
 直线与椭圆相切;
直线与椭圆相切;
 直线与双曲线相切;
直线与双曲线相切;
 直线与抛物线相切;
直线与抛物线相切;
(3)相离:
 直线与椭圆相离;
直线与椭圆相离;
 直线与双曲线相离;
直线与双曲线相离;
 直线与抛物线相离。
直线与抛物线相离。
特别提醒:(1)直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交。如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;
(2)过双曲线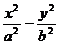 =1外一点
=1外一点 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。
如(1)过点 作直线与抛物线
作直线与抛物线 只有一个公共点,这样的直线有______
只有一个公共点,这样的直线有______
(2)过点(0,2)与双曲线 有且仅有一个公共点的直线的斜率的取值范围为______
有且仅有一个公共点的直线的斜率的取值范围为______
(3)对于抛物线C: ,我们称满足
,我们称满足 的点
的点 在抛物线的内部,
在抛物线的内部,
若点 在抛物线的内部,则直线
在抛物线的内部,则直线 :
: 与抛物线C的位置关系是_______
与抛物线C的位置关系是_______
(4)过抛物线 的焦点
的焦点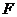 作一直线交抛物线于P、Q两点,若线段PF与FQ的长
作一直线交抛物线于P、Q两点,若线段PF与FQ的长
分别是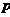 、
、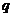 ,则
,则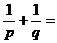 _______
_______
(5)设双曲线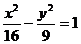 的右焦点为
的右焦点为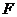 ,右准线为
,右准线为 ,设某直线
,设某直线 交其左支、右支和
交其左支、右支和
右准线分别于 ,则
,则 和
和 的大小关系为___________
的大小关系为___________
(6)求椭圆 上的点到直线
上的点到直线 的最短距离
的最短距离
(7)直线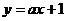 与双曲线
与双曲线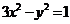 交于
交于 、
、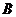 两点。①当
两点。①当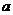 为何值时,
为何值时, 、
、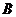 分
分
别在双曲线的两支上?②当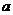 为何值时,以AB为直径的圆过坐标原点?
为何值时,以AB为直径的圆过坐标原点?
5、点 和椭圆
和椭圆 (
(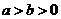 )的关系:
)的关系:
(1)点 在椭圆外
在椭圆外
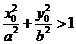 ;
;
(2)点 在椭圆上
在椭圆上
 =1;
=1;
(3)点 在椭圆内
在椭圆内

4.圆锥曲线的几何性质:
(1)椭圆(以 (
(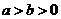 )为例):①范围:
)为例):①范围: ;②焦点:两个焦点
;②焦点:两个焦点 ;③对称性:两条对称轴
;③对称性:两条对称轴 ,一个对称中心(0,0),四个顶点
,一个对称中心(0,0),四个顶点 ,其中长轴长为2
,其中长轴长为2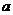 ,短轴长为2
,短轴长为2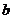 ;④准线:两条准线
;④准线:两条准线 ; ⑤离心率:
; ⑤离心率: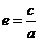 ,椭圆
,椭圆
 ,
, 越小,椭圆越圆;
越小,椭圆越圆; 越大,椭圆越扁。
越大,椭圆越扁。
如(1)若椭圆 的离心率
的离心率 ,则
,则 的值是_
_
的值是_
_
(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为_
(2)双曲线(以 (
( )为例):①范围:
)为例):①范围: 或
或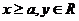 ;②焦点:两个焦点
;②焦点:两个焦点 ;③对称性:两条对称轴
;③对称性:两条对称轴 ,一个对称中心(0,0),两个顶点
,一个对称中心(0,0),两个顶点 ,其中实轴长为2
,其中实轴长为2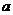 ,虚轴长为2
,虚轴长为2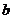 ,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为
,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为 ;④准线:两条准线
;④准线:两条准线 ; ⑤离心率:
; ⑤离心率: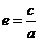 ,双曲线
,双曲线
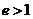 ,等轴双曲线
,等轴双曲线
 ,
, 越小,开口越小,
越小,开口越小, 越大,开口越大;⑥两条渐近线:
越大,开口越大;⑥两条渐近线: 。
。
如(1)双曲线的渐近线方程是 ,则该双曲线的离心率等于______
,则该双曲线的离心率等于______
(2)双曲线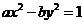 的离心率为
的离心率为 ,则
,则 =
=
(3)设双曲线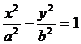 (a>0,b>0)中,离心率e∈[
(a>0,b>0)中,离心率e∈[ ,2],则两条渐近线夹角θ的取值范围是________
,2],则两条渐近线夹角θ的取值范围是________
(3)抛物线(以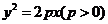 为例):①范围:
为例):①范围: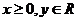 ;②焦点:一个焦点
;②焦点:一个焦点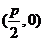 ,其中
,其中 的几何意义是:焦点到准线的距离;③对称性:一条对称轴
的几何意义是:焦点到准线的距离;③对称性:一条对称轴 ,没有对称中心,只有一个顶点(0,0);④准线:一条准线
,没有对称中心,只有一个顶点(0,0);④准线:一条准线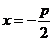 ; ⑤离心率:
; ⑤离心率: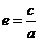 ,抛物线
,抛物线
 。
。
如设 ,则抛物线
,则抛物线 的焦点坐标为________
的焦点坐标为________
3.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):
(1)椭圆:由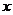
 ,
,
 分母的大小决定,焦点在分母大的坐标轴上。
分母的大小决定,焦点在分母大的坐标轴上。
如已知方程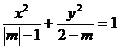 表示焦点在y轴上的椭圆,则m的取值范围是_ _
表示焦点在y轴上的椭圆,则m的取值范围是_ _
(2)双曲线:由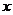
 ,
,
 项系数的正负决定,焦点在系数为正的坐标轴上;
项系数的正负决定,焦点在系数为正的坐标轴上;
(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
特别提醒:(1)在求解椭圆、双曲线问题时,首先要判断焦点位置,焦点F ,F
,F 的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数
的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数 ,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,
,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,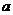 最大,
最大,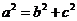 ,在双曲线中,
,在双曲线中, 最大,
最大,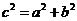 。
。
2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):
(1)椭圆:焦点在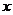 轴上时
轴上时 (
(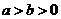 )
)
 (参数方程,其中
(参数方程,其中 为参数),焦点在
为参数),焦点在 轴上时
轴上时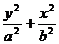 =1(
=1(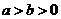 )。方程
)。方程 表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。
表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。
如(1)已知方程 表示椭圆,则
表示椭圆,则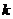 的取值范围为____
的取值范围为____
(2)若 ,且
,且 ,则
,则 的最大值是____,
的最大值是____,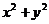 的最小值是___
的最小值是___
(2)双曲线:焦点在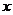 轴上:
轴上: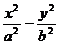 =1,焦点在
=1,焦点在 轴上:
轴上: =1(
=1( )。方程
)。方程 表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。
表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。
如(1)双曲线的离心率等于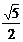 ,且与椭圆
,且与椭圆 有公共焦点,则该双曲线的方程_______
有公共焦点,则该双曲线的方程_______
(2)设中心在坐标原点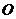 ,焦点
,焦点 、
、 在坐标轴上,离心率
在坐标轴上,离心率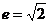 的双曲线C过点
的双曲线C过点 ,则C的方程为_______
,则C的方程为_______
(3)抛物线:开口向右时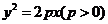 ,开口向左时
,开口向左时 ,开口向上时
,开口向上时 ,开口向下时
,开口向下时 。
。
1.圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F ,F
,F 的距离的和等于常数
的距离的和等于常数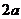 ,且此常数
,且此常数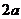 一定要大于
一定要大于 ,当常数等于
,当常数等于 时,轨迹是线段F
时,轨迹是线段F F
F ,当常数小于
,当常数小于 时,无轨迹;双曲线中,与两定点F
时,无轨迹;双曲线中,与两定点F ,F
,F 的距离的差的绝对值等于常数
的距离的差的绝对值等于常数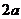 ,且此常数
,且此常数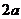 一定要小于|F
一定要小于|F F
F |,定义中的“绝对值”与
|,定义中的“绝对值”与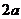 <|F
<|F F
F |不可忽视。若
|不可忽视。若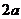 =|F
=|F F
F |,则轨迹是以F
|,则轨迹是以F ,F
,F 为端点的两条射线,若
为端点的两条射线,若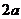 ﹥|F
﹥|F F
F |,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
|,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
如(1)已知定点 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.
,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A. B.
B.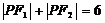
C.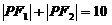 D.
D.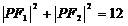
(2)方程 表示的曲线是_____
表示的曲线是_____
(2)第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母”,其商即是离心率 。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。
。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。
如已知点 及抛物线
及抛物线 上一动点P(x,y),则y+|PQ|的最小值是__ ___
上一动点P(x,y),则y+|PQ|的最小值是__ ___
2.(江苏卷18)设平面直角坐标系 中,设二次函数
中,设二次函数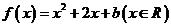 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(Ⅰ)求实数b 的取值范围;
(Ⅱ)求圆C 的方程;
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.
[解析]本小题主要考查二次函数图象与性质、圆的方程的求法.
(Ⅰ)令 =0,得抛物线与
=0,得抛物线与 轴交点是(0,b);
轴交点是(0,b);
令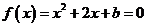 ,由题意b≠0 且Δ>0,解得b<1 且b≠0.
,由题意b≠0 且Δ>0,解得b<1 且b≠0.
(Ⅱ)设所求圆的一般方程为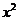

令 =0 得
=0 得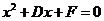 这与
这与 =0 是同一个方程,故D=2,F=
=0 是同一个方程,故D=2,F= .
.
令 =0 得
=0 得 =0,此方程有一个根为b,代入得出E=―b―1.
=0,此方程有一个根为b,代入得出E=―b―1.
所以圆C 的方程为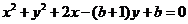 .
.
(Ⅲ)圆C 必过定点(0,1)和(-2,1).
证明如下:将(0,1)代入圆C 的方程,得左边=0 +1
+1 +2×0-(b+1)+b=0,右边=0,
+2×0-(b+1)+b=0,右边=0,
所以圆C 必过定点(0,1).
同理可证圆C 必过定点(-2,1).
18.(广东卷11)经过圆 的圆心
的圆心 ,且与直线
,且与直线 垂直的直线
垂直的直线
方程是 .
19已知菱形 的顶点
的顶点 在椭圆
在椭圆 上,对角线
上,对角线 所在直线的斜率为1.
所在直线的斜率为1.
(Ⅰ)当直线 过点
过点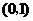 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)当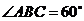 时,求菱形
时,求菱形 面积的最大值.
面积的最大值.
解:(Ⅰ)由题意得直线 的方程为
的方程为 .
.
因为四边形 为菱形,所以
为菱形,所以 .
.
于是可设直线 的方程为
的方程为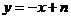 .
.
由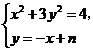 得
得 .
.
因为 在椭圆上,
在椭圆上,
所以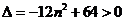 ,解得
,解得 .
.
设 两点坐标分别为
两点坐标分别为 ,
,
则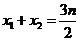 ,
, ,
,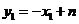 ,
, .
.
所以 .
.
所以 的中点坐标为
的中点坐标为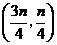 .
.
由四边形 为菱形可知,点
为菱形可知,点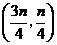 在直线
在直线 上,
上,
所以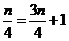 ,解得
,解得 .
.
所以直线 的方程为
的方程为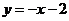 ,即
,即 .
.
(Ⅱ)因为四边形 为菱形,且
为菱形,且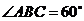 ,
,
所以 .
.
所以菱形 的面积
的面积 .
.
由(Ⅰ)可得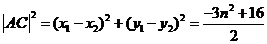 ,
,
所以 .
.
所以当 时,菱形
时,菱形 的面积取得最大值
的面积取得最大值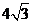 .
.
17.(重庆卷15)直线l与圆 (a<3)相交于两点A,B,弦AB的中点为(0,1),则直线l的方程为 . x-y+1=0
(a<3)相交于两点A,B,弦AB的中点为(0,1),则直线l的方程为 . x-y+1=0
16.(四川卷14)已知直线 与圆
与圆 ,则
,则 上各点到
上各点到 的距离的最小值为_______。
的距离的最小值为_______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com