
14.答案:B
解析: RM={x|x>1+
RM={x|x>1+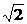 ,x∈R},又1+
,x∈R},又1+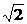 <3.
<3.
故 RM∩N={3,4}.故选B.
RM∩N={3,4}.故选B.
13.答案:B
解析:方法一:N={x|x2-2x-3<0}={x|-1<x<3},所以M∩N={x|0≤x<2},故选B.
方法二:由(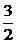 )2-2·(
)2-2·(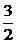 )-3<0,知1.5∈N,又1.5∈M,因此1.5∈M∩N,从而排除A、C;由交集定义与M的表达式,可排除D,得B.
)-3<0,知1.5∈N,又1.5∈M,因此1.5∈M∩N,从而排除A、C;由交集定义与M的表达式,可排除D,得B.
评述:本题考查对交集的理解和掌握,所设定的集合实质是不等式的解集,兼考处理不等式解集的基本技能.
12.答案:D
解析:由已知A={x|x>6或x<-1},B={x|5-a<x<5+a},而11∈B,
∴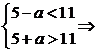 a>6.
a>6.
此时:5-a<-1,5+a>6,∴A∪B=R.
评述:本题考查集合基本知识,一元二次不等式、绝对值不等式的解法及分析问题解决问题的能力.
11.答案:C
解析:由图知阴影部分表示的集合是M∩P的子集且是 IS的子集,故答案为C.
IS的子集,故答案为C.
评述:本题源于课本,属送分题,是前几年高考题的回归.
10.答案:A
解析:根据子集的计算应有24-1=15(个).
评述:求真子集时千万不要忘记空集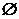 是任何非空集合的真子集.同时,A不是A的真子集.
是任何非空集合的真子集.同时,A不是A的真子集.
9.答案:A
解析:若a=1,则y=cos2x-sin2x=cos2x,此时y的最小正周期为π,故a=1是充分条件.
而由y=cos2ax-sin2ax=cos2ax,此时y的周期为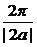 =π,
=π,
∴a=±1,故a=1不是必要条件.
评述:本题考查充要条件的基本知识,难点在于周期概念的准确把握.
8.答案:C
解析:∵A={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1}
B={-5,-4,-3,-2,-1,0,1,2,3,4,5}
∴A∪B={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5}共有16个元素.
7.答案:A
解析:∵ IM={b,e},
IM={b,e}, IN={a,c},∴
IN={a,c},∴ IM∩
IM∩ IN=
IN=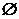 .
.
6.答案:C
解析:当a=3时,直线l1:3x+2y+9=0,直线l2:3x+2y+4=0
显然a=3 l1∥l2.
l1∥l2.
5.答案:D
解析:若a2+b2=0,即a=b=0时,f(-x)=(-x)|x+0|+0=-x|x|=-f(x)
∴a2+b2=0是f(x)为奇函数的充分条件.
又若f(x)为奇函数即f(-x)=-x|(-x)+a|+b=-(x|x+a|+b),则
必有a=b=0,即a2+b2=0,∴a2+b2=0是f(x)为奇函数的必要条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com