
24. 答案:D
答案:D
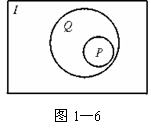
解析:依题意画出文氏图:如图1-6,显然A、B、C均正确,故应选D.
23.答案:C
解析:∵ IA={4},
IA={4}, IB={0,1},∴
IB={0,1},∴ IA∪
IA∪ IB={0,1,4}.
IB={0,1,4}.
22.答案:A
解析:如果方程ax2+by2=c表示双曲线,即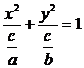 表示双曲线,因此有
表示双曲线,因此有 ,即ab<0.这就是说“ab<0”是必要条件;若ab<0,c可以为0,此时,方程不表示双曲线,即ab<0不是充分条件.
,即ab<0.这就是说“ab<0”是必要条件;若ab<0,c可以为0,此时,方程不表示双曲线,即ab<0不是充分条件.
评述:本题考查充要条件的推理判断和双曲线的概念.
21.答案:C
 解析一:∵M∩N=N,∴N
解析一:∵M∩N=N,∴N M,∴
M,∴ IN
IN
 IM
IM
解析二:画出韦恩图1-5,显然: IM
IM
 IN.故选C.
IN.故选C.
评述:本题主要考查集合的概念和集合的关系,题目中不给出具体集合,对分析问题解决问题能力提高了要求.
20.答案:B
解析:由已知 IM={-3,-4},∴
IM={-3,-4},∴ IM∩N={-3,-4}.
IM∩N={-3,-4}.
19.答案:B
解析:由集合P得1<x<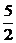 ,由集合Q有0<x<10.利用数轴上的覆盖关系,易得P
,由集合Q有0<x<10.利用数轴上的覆盖关系,易得P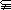 Q.
Q.
18.答案:D
解析:由奇函数定义可知:若f(x)为奇函数,则对定义域内任意一个x,都有f(-x)=-f(x),即f(-x)+f(x)=0,反之,若有f(x)+f(-x)=0,即f(-x)=-f(x),由奇函数的定义可知f(x)为奇函数.
评述:对于判断奇偶性问题应注意:x为定义域内任意值,因此定义域本身应关于原点对称,这是奇偶性问题的必要条件.
17.答案:C
解析:方法一: IA中元素是非2的倍数的自然数,
IA中元素是非2的倍数的自然数, IB中元素是非4的倍数的自然数,显然,只有C选项正确.
IB中元素是非4的倍数的自然数,显然,只有C选项正确.
 方法二:因A={2,4,6,8…},B={4,8,12,16,…},所以
方法二:因A={2,4,6,8…},B={4,8,12,16,…},所以 IB={1,2,3,5,6,7,9…},所以I=A∪
IB={1,2,3,5,6,7,9…},所以I=A∪ IB,故答案为C.
IB,故答案为C.
方法三:因B A,所以
A,所以 IA
IA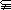
 IB,
IB, IA∩
IA∩ IB=
IB= IA,故I=
IA,故I=
A∪ IA=A∪
IA=A∪ IB.
IB.
方法四:根据题意,我们画出文氏图1-4来解,易知B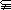 A,如图:可以清楚看到I=
A,如图:可以清楚看到I=
A∪ IB是成立的.
IB是成立的.
评述:本题考查对集合概念和关系的理解和掌握,注意数形结合的思想方法,用无限集考查,提高了对逻辑思维能力的要求.
16. 答案:C
答案:C
解析:方法一:显然 IB={1,2,4,6,7},
IB={1,2,4,6,7},
于是A∪ IB=I,故选C.
IB=I,故选C.
方法二:利用文氏图1-3知I=A∪ IB,应选C.
IB,应选C.
15.答案:D
解析:
方法一:解方程组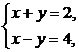 得
得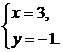 故M∩N={(3,-1)},所以选D.
故M∩N={(3,-1)},所以选D.
方法二:因所求M∩N为两个点集的交集,故结果仍为点集,显然只有D正确.
评述:要特别理解集合中代表元素的意义,此题迎刃而解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com