
(二) ①、[正宫][端正好] 没来由犯王法,不提防遭刑宪,叫声屈动地惊天。顷刻间游魂先赴森罗殿,怎不将天地也生怨。
[正宫]是 ,[端正好]是 ,这一段文字出自课文 ,作者是 (朝代)的 。
②、 是戏剧动作的总称。包括舞台的程式、武打和舞蹈。
③宋词又叫 或 。依照风格一般分为 与 。
7.(一)①、大江东去,浪淘尽,千古风流人物。故垒西边,人道是,三国周郎赤壁。 , , 。江山如画,一时多少豪杰。
②、东篱把酒黄昏后,有暗香盈袖。 , , 。
③、竹杖芒鞋轻胜马,谁怕? 。
④、可堪回首,佛狸祠下,一片神鸦社鼓!凭谁问: , ?
⑤ ,水随天去秋无际。
⑥、 ,到黄昏、点点滴滴。这次第, ?
3、下列划线字词在文中解释不完全正确的一项是( )
A、戕害(杀害、残害) 都门帐饮无绪(没有心思、心情不好)
还酹江月(把酒洒在地上,以示凭吊) 经年(年复一年)
B、舞榭(建在高台上的房子) 这次第(光景、状况)
蟊贼(吃禾苗根、节的害虫。 怎生了得(怎么包含得了)
在文中指危害人民或国家的人)
C、断鸿(失群的孤雁) 一尊还酹(同“樽”,酒杯)
净(元杂剧中扮演性情恶劣、举动粗野的角色)
仙吕(元杂剧的宫调名) 采茶歌(曲牌名)
D、三秋(秋季) 珠玑(泛指大小不同的各种珠宝)
月一十五(每月初一、十五) 孟浪(鲁莽草率)
2、下列词语中有错别字的一项是( )
A、嗟怨 篡夺 枭雄 前合后偃
B、错勘 珠玑 凝噎 引亢高歌
C、樯橹 料峭 堪脍 小乔初嫁
D、罪愆 盗跖 昧心 暮霭沉沉
1、下列加点字注音全对的一项是( )
A、看觑(qù) 窥伺(cì) 蟊贼(máo) 湛湛青天(zhàn)
B、涔涔(cén) 亲戚(qī) 缜密(zhěn) 鳏寡孤独(guān)
C、戕害(qiāng) 纶巾(guān) 尸骸(hái) 繁文缛节(rù)
D、揩干(jiē) 亢旱(kàn) 埋怨(mán) 还酹江月(lèi)
23.[解法一](1)由 ,得
,得 ,
......2分
,
......2分
整理后,可得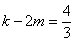 ,
,
 、
、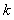

 ,
,
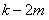 为整数,
为整数, 
 不存在
不存在 、
、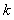

 ,使等式成立。
......5分
,使等式成立。
......5分
(2)若 ,即
,即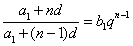 ,
(*)
,
(*)
(ⅰ)若 则
则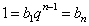 。
。 
当{ }为非零常数列,{
}为非零常数列,{ }为恒等于1的常数列,满足要求。
......7分
}为恒等于1的常数列,满足要求。
......7分
(ⅱ)若 ,(*)式等号左边取极限得
,(*)式等号左边取极限得 ,(*)式等号右边的极限只有当
,(*)式等号右边的极限只有当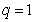 时,才能等于1。此时等号左边是常数,
时,才能等于1。此时等号左边是常数, ,矛盾。
,矛盾。
综上所述,只有当{ }为非零常数列,{
}为非零常数列,{ }为恒等于1的常数列,满足要求。......10分
}为恒等于1的常数列,满足要求。......10分
[解法二]设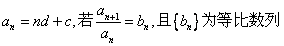

则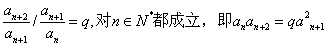


(i) 若d=0,则

(ii) 若
 (常数)即
(常数)即 ,则d=0,矛盾
,则d=0,矛盾
综上所述,有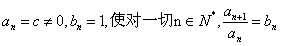 , 10分
, 10分
(3)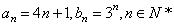

设 .
.
 ,
,
 .
13分
.
13分
取 15分
15分
由二项展开式可得正整数M1、M2,使得(4-1)2s+2=4M1+1,
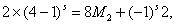

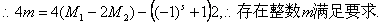
故当且仅当p=3s,s N时,命题成立.
N时,命题成立.
说明:第(3)题若学生从以下角度解题,可分别得部分分(即分步得分)
若p为偶数,则am+1+am+2+……+am+p为偶数,但3k为奇数
故此等式不成立,所以,p一定为奇数。
当p=1时,则am+1=bk,即4m+5=3k,
而3k=(4-1)k
=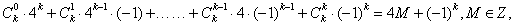
当k为偶数时,存在m,使4m+5=3k成立 1分
当p=3时,则am+1+am+2+am+3=bk,即3am+2-bk, 
也即3(4m+9)=3k,所以4m+9=3k-1,4(m+1)+5=3k-1
由已证可知,当k-1为偶数即k为奇数时,存在m, 4m+9=3k成立 2分
当p=5时,则am+1+am+2+……+am+5=bk,即5am+3=bk
也即5(4m+13)=3k,而3k不是5的倍数,所以,当p=5时,所要求的m不存在
故不是所有奇数都成立. 2分

23.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知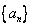 是公差为
是公差为 的等差数列,
的等差数列, 是公比为
是公比为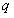 的等比数列。
的等比数列。
(1) 若 ,是否存在
,是否存在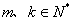 ,有
,有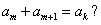 说明理由;
说明理由; 

(2) 找出所有数列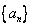 和
和 ,使对一切
,使对一切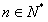 ,
, ,并说明理由;
,并说明理由;
(3) 若 试确定所有的
试确定所有的 ,使数列
,使数列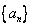 中存在某个连续
中存在某个连续 项的和是数列
项的和是数列 中的一项,请证明。
中的一项,请证明。
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
已知函数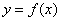 的反函数。定义:若对给定的实数
的反函数。定义:若对给定的实数 ,函数
,函数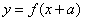 与
与 互为反函数,则称
互为反函数,则称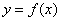 满足“
满足“ 和性质”;若函数
和性质”;若函数 与
与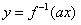 互为反函数,则称
互为反函数,则称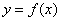 满足“
满足“ 积性质”。
积性质”。
(1) 判断函数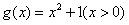 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由; 

(2) 求所有满足“2和性质”的一次函数;
(3) 设函数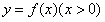 对任何
对任何 ,满足“
,满足“ 积性质”。求
积性质”。求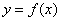 的表达式。
的表达式。
22(1)解,函数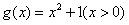 的反函数是
的反函数是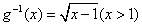
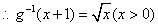


而 其反函数为
其反函数为

故函数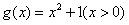 不满足“1和性质”
不满足“1和性质”
(2)设函数 满足“2和性质”,
满足“2和性质”,
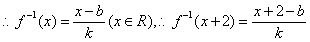 …….6分
…….6分
而 得反函数
得反函数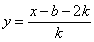 ………….8分
………….8分
由“2和性质”定义可知 =
= 对
对 恒成立
恒成立
 即所求一次函数为
即所求一次函数为 ………..10分
………..10分 
(3)设 ,
, ,且点
,且点 在
在 图像上,则
图像上,则 在函数
在函数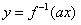 图象上,
图象上,
 故
故 ,可得
,可得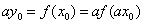 ,
......12分
,
......12分
 ,
, 

令 ,则
,则 。
。
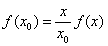 ,即
,即 。 ......14分
。 ......14分
综上所述,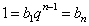
 ,此时
,此时 ,其反函数就是
,其反函数就是 ,
,
而 ,故
,故 与
与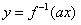 互为反函数 。
......16分
互为反函数 。
......16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com