
15.(2009四川卷理)已知 为实数,且
为实数,且 。则“
。则“ ”是“
”是“ ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C.充要条件
D. 既不充分也不必要条件. 

[考点定位]本小题考查不等式的性质、简单逻辑,基础题。(同文7)
解析: 推不出
推不出 ;但
;但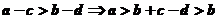 ,故选择B。
,故选择B。
解析2:令 ,则
,则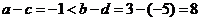 ;由
;由 可得,
可得,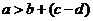 因为
因为 ,则
,则 ,所以
,所以 。故“
。故“ ”是“
”是“ ”的必要而不充分条件。
”的必要而不充分条件。
14.(2009天津卷理)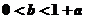 ,若关于x 的不等式
,若关于x 的不等式 >
>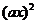 的解集中的整数恰有3个,则
的解集中的整数恰有3个,则
(A) (B)
(B)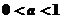 (C)
(C)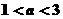 (D)
(D)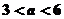
[考点定位]本小题考查解一元二次不等式,
解析:由题得不等式 >
>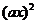 即
即 ,它的解应在两根之间,故有
,它的解应在两根之间,故有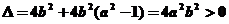 ,不等式的解集为
,不等式的解集为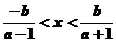 或
或 。若不等式的解集为
。若不等式的解集为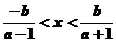 ,又由
,又由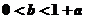 得
得 ,故
,故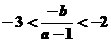 ,即
,即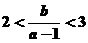 .
. 

13.(2009天津卷理)设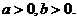 若
若 的最小值为
的最小值为
A 8
B 4 C
1 D 
[考点定位]本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
[解析]因为 ,所以
,所以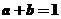 ,
,
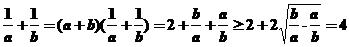 ,当且仅当
,当且仅当 即
即 时“=”成立,故选择C
时“=”成立,故选择C
12.(2009天津卷理)设变量x,y满足约束条件: .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为
(A)6 (B)7 (C)8 (D)23
[考点定位]本小考查简单的线性规划,基础题。
解析:画出不等式 表示的可行域,如右图,.
表示的可行域,如右图,. 

让目标函数表示直线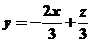 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组 得
得 ,所以
,所以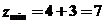 ,故选择B。.
,故选择B。. 


11.(2009湖南卷理)已知D是由不等式组 ,所确定的平面区域,则圆
,所确定的平面区域,则圆  在区域D内
在区域D内
的弧长为 [ B]
A  B
B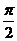 C
C 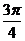 D
D
 .
. 

[答案]:B
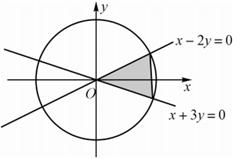
[解析]解析如图示,图中阴影部分所在圆心角所对弧长即为所求,易知图中两直线的斜率分别是
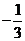 ,所以圆心角
,所以圆心角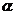 即为两直线的所成夹角,所以
即为两直线的所成夹角,所以 ,所以
,所以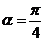 ,而圆的半径是2,所以弧长是
,而圆的半径是2,所以弧长是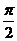 ,故选B现。
,故选B现。
10.(2009宁夏海南卷文)设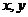 满足
满足 则
则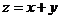
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值
(D)既无最小值,也无最大值. 

[答案]B
[解析]画出不等式表示的平面区域,如右图,由z=x+y,得y=-x+z,令z=0,画出y=-x的图象,当它的平行线经过A(2,0)时,z取得最小值,最小值为:z=2,无最大值,故选.B

9.(2009宁夏海南卷理)设x,y满足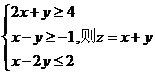
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值 (D)既无最小值,也无最大值
解析:画出可行域可知,当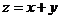 过点(2,0)时,
过点(2,0)时, ,但无最大值。选B.
,但无最大值。选B.
8.(2009湖南卷文)若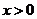 ,则
,则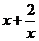 的最小值为
的最小值为
 .
.
解: 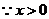
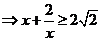 ,当且仅当
,当且仅当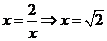 时取等号.
时取等号.
7.(2009四川卷文)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么该企业可获得最大利润是
A. 12万元 B. 20万元 C. 25万元 D. 27万元
[答案]D
 [解析]设生产甲产品
[解析]设生产甲产品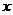 吨,生产乙产品
吨,生产乙产品 吨,则有关系:
吨,则有关系:
|
|
A原料 |
B原料 |
甲产品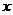 吨 吨 |
3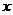 |
2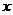 |
乙产品 吨 吨 |
 |
3 |
则有:
目标函数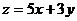
作出可行域后求出可行域边界上各端点的坐标,经验证知:
当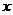 =3,
=3, =5时可获得最大利润为27万元,故选D
=5时可获得最大利润为27万元,故选D
6.(2009四川卷文)已知 ,
,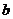 ,
, ,
,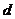 为实数,且
为实数,且 >
>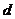 .则“
.则“ >
>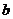 ”是“
”是“ -
- >
>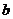 -
-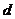 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
[答案]B .


[解析]显然,充分性不成立.又,若 -
- >
>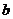 -
-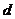 和
和 >
>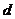 都成立,则同向不等式相加得
都成立,则同向不等式相加得 >
>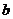
即由“ -
- >
>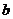 -
-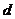 ”
”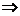 “
“ >
>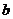 ”
”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com