
18.(江西卷)(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是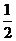 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令 表示该公司的资助总额.
表示该公司的资助总额.
(1) 写出 的分布列; (2) 求数学期望
的分布列; (2) 求数学期望 .
. 

解:(1) 的所有取值为
的所有取值为
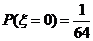

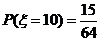

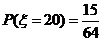


(2) .
.
16、(全国卷2)20(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数;
(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求 的分布列及数学期望。
的分布列及数学期望。 

分析:(I)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意此分层抽样与性别无关。
(II)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率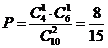
(III) 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
, ,
,
 ,
,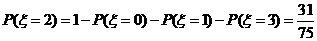
分布列及期望略。
评析:本题较常规,比08年的概率统计题要容易。在计算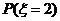 时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
15、(山东卷) (19)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q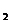 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 |
0
|
2
|
3 |
4 |
5 |
  p p
|
0.03
|
P1
|
P2 |
P3
|
P4
|
(1)
求q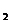 的值;
的值; 

(2)
求随机变量 的数学期望E
的数学期望E ;
;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
解:(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25, , P(B)= q
, P(B)= q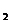 ,
, .
.
根据分布列知:  =0时
=0时 =0.03,所以
=0.03,所以 ,q
,q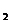 =0.8.
=0.8.
(2)当 =2时, P1=
=2时, P1=


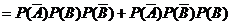 =0.75 q
=0.75 q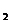 (
(  )×2=1.5 q
)×2=1.5 q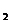 (
(  )=0.24
)=0.24
当 =3时, P2 =
=3时, P2 = =0.01,
=0.01,
当 =4时, P3=
=4时, P3=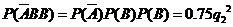 =0.48,
=0.48,
当 =5时, P4=
=5时, P4=
 =0.24
=0.24
所以随机变量 的分布列为
的分布列为
 |
0
|
2
|
3 |
4 |
5 |
|
p
|
0.03
|
0.24
|
0.01 |
0.48
|
0.24 |
随机变量 的数学期望
的数学期望
(3)该同学选择都在B处投篮得分超过3分的概率为

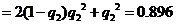 ;
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
[命题立意]:本题主要考查了互斥事件的概率,相互独立事件的概率和数学期望,以及运用概率知识解决问题的能力.
14、(全国1)19.(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局。
(I)求甲获得这次比赛胜利的概率;
(II)设 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求 得分布列及数学期望。
得分布列及数学期望。
分析:本题较常规,比08年的概率统计题要容易。
需提醒的是:认真审题是前提,部分考生由于考虑了前两局的概率而导致失分,这是很可惜的,主要原因在于没读懂题。
另外,还要注意表述,这也是考生较薄弱的环节。
13、(辽宁卷)(19)(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为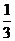 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) 

(19)解:
(Ⅰ)依题意X的分列为

………………6分
(Ⅱ)设A1表示事件“第一次击中目标时,击中第i部分”,i=1,2.
B1表示事件“第二次击中目标时,击中第i部分”,i=1,2.
依题意知P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3,
 ,
,
所求的概率为
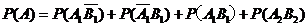

 ………12分
………12分
12、(浙江卷)
|
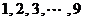 这
这 个自然数中,任取
个自然数中,任取 个数.
个数.
(I)求这 个数中恰有
个数中恰有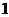 个是偶数的概率;
个是偶数的概率;
(II)设 为这
为这 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为 ,则有两组相邻的数
,则有两组相邻的数
 和
和 ,此时
,此时 的值是
的值是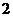 ).求随机变量
).求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.
解析:(I)记“这3个数恰有一个是偶数”为事件A,则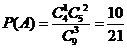 ;
; 

(II)随机变量 的取值为
的取值为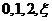 的分布列为
的分布列为
 |
0 |
1 |
2 |
|
P |
 |
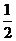 |
 |
所以 的数学期望为
的数学期望为


11、(天津卷)(18)(本小题满分12分)
在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
本小题主要考查古典概型及计算公式、离散型随机变量的分布列和数学期望、互斥事件等基础知识,考查运用概率知识解决实际问题的能力。满分12分。
(Ⅰ)解:由于从10件产品中任取3件的结果为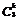 ,从10件产品中任取3件,其中恰有k件一等品的结果数为
,从10件产品中任取3件,其中恰有k件一等品的结果数为 ,那么从10件产品中任取3件,其中恰有k件一等品的概率为P(X=k)=
,那么从10件产品中任取3件,其中恰有k件一等品的概率为P(X=k)= 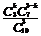 ,k=0,1,2,3.
,k=0,1,2,3.
所以随机变量X的分布列是
|
X |
0 |
1 |
2 |
3 |
|
P |
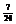 |
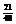 |
 |
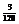 |
X的数学期望EX=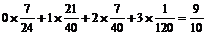
(Ⅱ)解:设“取出的3件产品中一等品件数多于二等品件数”为事件A,“恰好取出1件一等品和2件三等品”为事件A1“恰好取出2件一等品“为事件A2,”恰好取出3件一等品”为事件A3由于事件A1,A2,A3彼此互斥,且A=A1∪A2∪A3而
 P(A2)=P(X=2)=
P(A2)=P(X=2)=  ,P(A3)=P(X=3)=
,P(A3)=P(X=3)=  ,
,
所以取出的3件产品中一等品件数多于二等品件数的概率为
P(A)=P(A1)+P(A2)+P(A3)=
 +
+ +
+ =
=
10、(四川卷)18. (本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有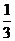 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡。
持银卡。
(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望 。
。
(18)本小题主要考察相互独立事件、互斥事件、随机变量的分布列、数学期望等概率计算,考察运用概率只是解决实际问题的能力。
解:(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。设事件 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件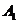 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件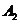 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。




所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是 。
。
…………………………………………………………6分
(Ⅱ) 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
, 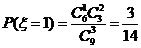
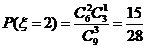 ,
, ,
,
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
 |
 |
 |
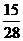 |
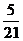 |
所以 , ……………………12分
, ……………………12分
9、(重庆卷)17.(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和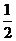 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数 的分布列与期望.w.w.
的分布列与期望.w.w.
(17)(本小题13分)
解:设 表示甲种大树成活k株,k=0,1,2
表示甲种大树成活k株,k=0,1,2
 表示乙种大树成活l株,l=0,1,2
表示乙种大树成活l株,l=0,1,2
则 ,
, 独立. 由独立重复试验中事件发生的概率公式有
独立. 由独立重复试验中事件发生的概率公式有
 ,
,  .
.
据此算得
 ,
,  ,
,  .
.
 ,
,  ,
,  .
.
(Ⅰ) 所求概率为
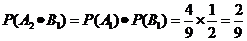 .
.
(Ⅱ) 解法一:
 的所有可能值为0,1,2,3,4,且
的所有可能值为0,1,2,3,4,且
 ,
,
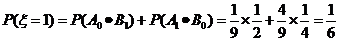 ,
,

=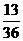 ,
,
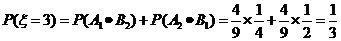 .
.
 .
.
综上知 有分布列
有分布列
 |
0 |
1 |
2 |
3 |
4 |
|
P |
1/36 |
1/6 |
13/36 |
1/3 |
1/9 |
从而, 的期望为
的期望为
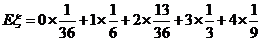
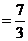 (株)
(株)
解法二:
分布列的求法同上
令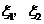 分别表示甲乙两种树成活的株数,则
分别表示甲乙两种树成活的株数,则


故有
从而知
8、(重庆卷)6.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为( C )
A. B.
B. C.
C. D.
D.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com