
2. ;
;
1.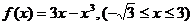 ;
;
3.等比数列的性质
①等比数列任意两项间的关系:如果 是等比数列的第
是等比数列的第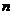 项,
项,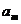 是等差数列的第
是等差数列的第 项,且
项,且 ,公比为
,公比为 ,则有
,则有 ;
;
②对于等比数列 ,若
,若 ,则
,则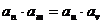 ,也就是:
,也就是: ,如图所示:
,如图所示: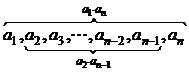 。
。
③若数列 是等比数列,
是等比数列, 是其前n项的和,
是其前n项的和, ,那么
,那么 ,
,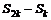 ,
,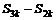 成等比数列。
成等比数列。
如下图所示:

2.等比数列的判定方法
①定义法:对于数列 ,若
,若 ,则数列
,则数列 是等比数列;
是等比数列;
②等比中项:对于数列 ,若
,若 ,则数列
,则数列 是等比数列。
是等比数列。
1.等比数列的知识要点(可类比等差数列学习)
(1)掌握等比数列定义 =q(常数)(n
=q(常数)(n N),同样是证明一个数列是等比数列的依据,也可由an·an+2=
N),同样是证明一个数列是等比数列的依据,也可由an·an+2=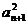 来判断;
来判断;
(2)等比数列的通项公式为an=a1·qn-1;
(3)对于G 是a、b 的等差中项,则G2=ab,G=± ;
;
(4)特别要注意等比数列前n 项和公式应分为q=1与q≠1两类,当q=1时,Sn=na1,当q≠1时,Sn= ,Sn=
,Sn= 。
。
题型1:等比数列的概念
例1.“公差为0的等差数列是等比数列”;“公比为 的等比数列一定是递减数列”;“a,b,c三数成等比数列的充要条件是b2=ac”;“a,b,c三数成等差数列的充要条件是2b=a+c”,以上四个命题中,正确的有( )
的等比数列一定是递减数列”;“a,b,c三数成等比数列的充要条件是b2=ac”;“a,b,c三数成等差数列的充要条件是2b=a+c”,以上四个命题中,正确的有( )
A.1个 B.2个 C.3个 D.4个
解析:四个命题中只有最后一个是真命题。
命题1中未考虑各项都为0的等差数列不是等比数列;
命题2中可知an+1=an× ,an+1<an未必成立,当首项a1<0时,an<0,则
,an+1<an未必成立,当首项a1<0时,an<0,则 an>an,即an+1>an,此时该数列为递增数列;
an>an,即an+1>an,此时该数列为递增数列;
命题3中,若a=b=0,c∈R,此时有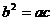 ,但数列a,b,c不是等比数列,所以应是必要而不充分条件,若将条件改为b=
,但数列a,b,c不是等比数列,所以应是必要而不充分条件,若将条件改为b=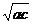 ,则成为不必要也不充分条件。
,则成为不必要也不充分条件。
点评:该题通过一些选择题的形式考察了有关等比数列的一些重要结论,为此我们要注意一些有关等差数列、等比数列的重要结论。
例2.命题1:若数列{an}的前n项和Sn=an+b(a≠1),则数列{an}是等比数列;
命题2:若数列{an}的前n项和Sn=an2+bn+c(a≠0),则数列{an}是等差数列;
命题3:若数列{an}的前n项和Sn=na-n,则数列{an}既是等差数列,又是等比数列;上述三个命题中,真命题有( )
A.0个 B.1个 C.2个 D.3个
解析:
由命题1得,a1=a+b,当n≥2时,an=Sn-Sn-1=(a-1)·an-1。若{an}是等比数列,则 =a,即
=a,即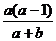 =a,所以只有当b=-1且a≠0时,此数列才是等比数列。
=a,所以只有当b=-1且a≠0时,此数列才是等比数列。
由命题2得,a1=a+b+c,当n≥2时,an=Sn-Sn-1=2na+b-a,若{an}是等差数列,则a2-a1=2a,即2a-c=2a,所以只有当c=0时,数列{an}才是等差数列。
由命题3得,a1=a-1,当n≥2时,an=Sn-Sn-1=a-1,显然{an}是一个常数列,即公差为0的等差数列,因此只有当a-1≠0;即a≠1时数列{an}才又是等比数列。
点评:等比数列中通项与求和公式间有很大的联系,上述三个命题均涉及到Sn与an的关系,它们是an=
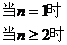 ,正确判断数列{an}是等差数列或等比数列,都必须用上述关系式,尤其注意首项与其他各项的关系。上述三个命题都不是真命题,选择A。
,正确判断数列{an}是等差数列或等比数列,都必须用上述关系式,尤其注意首项与其他各项的关系。上述三个命题都不是真命题,选择A。
题型2:等比数列的判定
例3.(2000全国理,20)(Ⅰ)已知数列{cn},其中cn=2n+3n,且数列{cn+1-pcn}为等比数列,求常数p;(Ⅱ)设{an}、{bn}是公比不相等的两个等比数列,cn=an+bn,证明数列{cn}不是等比数列。
解析:(Ⅰ)解:因为{cn+1-pcn}是等比数列,
故有:(cn+1-pcn)2=(cn+2-pcn+1)(cn-pcn-1),
将cn=2n+3n代入上式,得:
[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)],
即[(2-p)2n+(3-p)3n]2
=[(2-p)2n+1+(3-p)3n+1][(2-p)2n-1+(3-p)3n-1],
整理得 (2-p)(3-p)·2n·3n=0,解得p=2或p=3。
(2-p)(3-p)·2n·3n=0,解得p=2或p=3。
(Ⅱ)证明:设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn。
为证{cn}不是等比数列只需证c22≠c1·c3。
事实上,c22=(a1p+b1q)2=a12p2+b12q2+2a1b1pq,
c1·c3=(a1+b1)(a1p2+b1q2)=a12p2+b12q2+a1b1(p2+q2),
由于p≠q,p2+q2>2pq,又a1、b1不为零,
因此c22≠c1·c3,故{cn}不是等比数列。
点评:本题主要考查等比数列的概念和基本性质,推理和运算能力。
例4.(2003京春,21)如图3-1,在边长为l的等边△ABC中,圆O1为△ABC的 内切圆,圆O2与圆O1外切,且与AB,BC相切,…,圆On+1与圆On外切,且与AB、BC相切,如此无限继续下去.记圆On的面积为an(n∈N*),证明{an}是等比数列;
内切圆,圆O2与圆O1外切,且与AB,BC相切,…,圆On+1与圆On外切,且与AB、BC相切,如此无限继续下去.记圆On的面积为an(n∈N*),证明{an}是等比数列;
证明:记rn为圆On的半径,则r1= tan30°=
tan30°= 。
。 =sin30°=
=sin30°= ,所以rn=
,所以rn=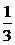 rn-1(n≥2),于是a1=πr12=
rn-1(n≥2),于是a1=πr12= ,故{an}成等比数列。
,故{an}成等比数列。
点评:该题考察实际问题的判定,需要对实际问题情景进行分析,最终对应数值关系建立模型加以解析。
题型3:等比数列的通项公式及应用
例5.一个等比数列有三项,如果把第二项加上4,那么所得的三项就成为等差数列,如果再把这个等差数列的第三项加上32,那么所得的三项又成为等比数列,求原来的等比数列。
解析:设所求的等比数列为a,aq,aq2;
则2(aq+4)=a+aq2,且(aq+4)2=a(aq2+32);
解得a=2,q=3或a= ,q=-5;
,q=-5;
故所求的等比数列为2,6,18或 ,-
,- ,
,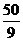 。
。
点评:第一种解法利用等比数列的基本量 ,先求公比,后求其它量,这是解等差数列、等比数列的常用方法,其优点是思路简单、实用,缺点是有时计算较繁。
,先求公比,后求其它量,这是解等差数列、等比数列的常用方法,其优点是思路简单、实用,缺点是有时计算较繁。
例6.(2006年陕西卷)已知正项数列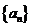 ,其前
,其前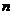 项和
项和 满足
满足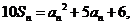 且
且 成等比数列,求数列
成等比数列,求数列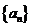 的通项
的通项
解析:∵10Sn=an2+5an+6, ①
∴10a1=a12+5a1+6,解之得a1=2或a1=3。
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2)。
当a1=3时,a3=13,a15=73,a1, a3,a15不成等比数列
∴a1≠3;
当a1=2时,,a3=12, a15=72,有 a32=a1a15 , ∴a1=2, ∴an=5n-3。
点评:该题涉及等比数列的求和公式与等比数列通项之间的关系,最终求得结果。
题型4:等比数列的求和公式及应用
例7.(1)(2006年辽宁卷)在等比数列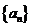 中,
中,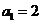 ,前
,前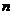 项和为
项和为 ,若数列
,若数列 也是等比数列,则
也是等比数列,则 等于( )
等于( )
A. B.
B.  C.
C. D.
D.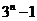
(2)(2006年北京卷)设 ,则
,则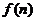 等于( )
等于( )
A.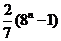 B.
B.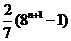 C.
C. D.
D.
(3)(1996全国文,21)设等比数列{an}的前n项和为Sn,若S3+S6=2S9,求数列的公比q;解析:(1)因数列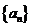 为等比,则
为等比,则 ,因数列
,因数列 也是等比数列,
也是等比数列,
则
即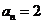 ,所以
,所以 ,故选择答案C。
,故选择答案C。
(2)D;
(3)解:若q=1,则有S3=3a1,S6=6a1,S9=9a1。
因a1≠0,得S3+S6≠2S9,显然q=1与题设矛盾,故q≠1。
由S3+S6=2S9,得 ,整理得q3(2q6-q3-1)=0,由q≠0,得2q6-q3-1=0,从而(2q3+1)(q3-1)=0,因q3≠1,故q3=-
,整理得q3(2q6-q3-1)=0,由q≠0,得2q6-q3-1=0,从而(2q3+1)(q3-1)=0,因q3≠1,故q3=- ,所以q=-
,所以q=- 。
。
点评:对于等比数列求和问题要先分清数列的通项公式,对应好首项和公比求出最终结果即可。
例8.(1)(2002江苏,18)设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2b4=a3.分别求出{an}及{bn}的前10项的和S10及T10;
(2)(2001全国春季北京、安徽,20)在1与2之间插入n个正数a1,a2,a3……,an,使这n+2个数成等比数列;又在1与2之间插入n个正数b1,b2,b3,……,bn,使这n+2个数成等差数列.记An=a1a2a3……an,Bn=b1+b2+b3+……+bn.
(Ⅰ)求数列{An}和{Bn}的通项;
(Ⅱ)当n≥7时,比较An与Bn的大小,并证明你的结论。
(3)(2002天津理,22)已知{an}是由非负整数组成的数列,满足a1=0,a2=3,
an+1an=(an-1+2)(an-2+2),n=3,4,5,….
(Ⅰ)求a3;
(Ⅱ)证明an=an-2+2,n=3,4,5,…;
(Ⅲ)求{an}的通项公式及其前n项和Sn。
解析:(1)∵{an}为等差数列,{bn}为等比数列,
∴a2+a4=2a3,b2b4=b32.
已知a2+a4=b3,b2b4=a3,
∴b3=2a3,a3=b32.
得 b3=2b32.
∵b3≠0 ∴b3= ,a3=
,a3=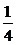 .
.
由a1=1,a3=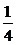 知{an}的公差为d=
知{an}的公差为d=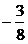 ,
,
∴S10=10a1+ .
.
由b1=1,b3= 知{bn}的公比为q=
知{bn}的公比为q= 或q=
或q= .
.
当q= 时,
时, ,
,
当q= 时,
时,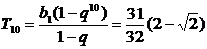 。
。
(2)(Ⅰ)设公比为q,公差为d,等比数列1,a1,a2,……,an,2,等差数列1,b1,b2,……,bn,2。
则A1=a1=1·q A2=1·q·1·q2 A3=1·q·1·q2·1·q3
又∵an+2=1·qn+1=2得qn+1=2,
An=q·q2…qn=q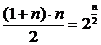 (n=1,2,3…)
(n=1,2,3…)
又∵bn+2=1+(n+1)d=2 ∴(n+1)d=1
B1=b1=1+d B2=b2+b1=1+d+1+2d Bn=1+d+…+1+nd= n
n
(Ⅱ)An>Bn,当n≥7时
证明:当n=7时,23.5=8·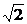 =An Bn=
=An Bn= ×7,∴An>Bn
×7,∴An>Bn
设当n=k时,An>Bn,则当n=k+1时,

又∵Ak+1=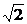 ·
·
 且Ak>Bk ∴Ak+1>
且Ak>Bk ∴Ak+1>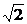 ·
· k
k
∴Ak+1-Bk+1>
又∵k=8,9,10… ∴Ak+1-Bk+1>0,综上所述,An>Bn成立.
(3)(Ⅰ)解:由题设得a3a4=10,且a3、a4均为非负整数,所以a3的可能的值为1,2,5,10.
若a3=1,则a4=10,a5= ,与题设矛盾.
,与题设矛盾.
若a3=5,则a4=2,a5=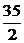 ,与题设矛盾.
,与题设矛盾.
若a3=10,则a4=1,a5=60,a6=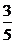 ,与题设矛盾.
,与题设矛盾.
所以a3=2.
(Ⅱ)用数学归纳法证明:
①当n=3,a3=a1+2,等式成立;
②假设当n=k(k≥3)时等式成立,即ak=ak-2+2,由题设ak+1ak=(ak-1+2)·(ak-2+2),因为ak=ak-2+2≠0,所以ak+1=ak-1+2,
也就是说,当n=k+1时,等式ak+1=ak-1+2成立;
根据①和②,对于所有n≥3,有an+1=an-1+2。
(Ⅲ)解:由a2k-1=a2(k-1)-1+2,a1=0,及a2k=a2(k-1)+2,a2=3得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,…,即an=n+(-1)n,n=1,2,3,…。
所以Sn=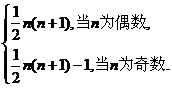
点评:本小题主要考查数列与等差数列前n项和等基础知识,以及准确表述,分析和解决问题的能力。
题型5:等比数列的性质
例9.(1)(2005江苏3)在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=( )
(A)33 (B)72 (C)84 (D)189
(2)(2000上海,12)在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N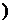 成立.类比上述性质,相应地:在等比数列{bn}中,若b9=1,则有等式 成立。
成立.类比上述性质,相应地:在等比数列{bn}中,若b9=1,则有等式 成立。
解析:(1)答案:C;解:设等比数列{an}的公比为q(q>0),由题意得:a1+a2+a3=21,即3+3q+3q2=21,q2+q-6=0,求得q=2(q=-3舍去),所以a3+a4+a5=q2(a1+a2+a3)=4 故选C。
故选C。
(2)答案:b1b2…bn=b1b2…b17-n(n<17,n∈N*);
解:在等差数列{an}中,由a10=0,得a1+a19=a2+a18=…=an+a20-n=an+1+a19-n=2a10=0,
所以a1+a2+…+an+…+a19=0,即a1+a2+…+an=-a19-a18-…-an+1,
又∵a1=-a19,a2=-a18,…,a19-n=-an+1
∴a1+a2+…+an=-a19-a18-…-an+1=a1+a2+…+a19-n,
若a9=0,同理可得a1+a2+…+an=a1+a2+a17-n,
相应地等比数列{bn}中,则可得:b1b2…bn=b1b2…b17-n(n<17,n∈N*)。
点评:本题考查了等比数列的相关概念及其有关计算能力。
例10.(1)设首项为正数的等比数列,它的前n项和为80,前2n项和为6560,且前n项中数值最大的项为54,求此数列的首项和公比q。
(2)在 和
和 之间插入n个正数,使这
之间插入n个正数,使这 个数依次成等比数列,求所插入的n个数之积。
个数依次成等比数列,求所插入的n个数之积。
(3)设等比数列{an}的各项均为正数,项数是偶数,它的所有项的和等于偶数项和的4倍,且第二项与第四项的积是第3项与第4项和的9倍,问数列{lgan}的前多少项和最大?(lg2=0 3,lg3=0.4)
3,lg3=0.4)
解析:(1)设等比数列{an}的前n项和为Sn,依题意设:a1>0,Sn=80 ,S2n=6560。
∵S2n≠2Sn ,∴q≠1;
从而
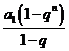 =80,且
=80,且 =6560。
=6560。
两式相除得1+qn=82 ,即qn=81。
∴a1=q-1>0 即q>1,从而等比数列{an}为递增数列,故前n项中数值最大的项为第n项。
∴a1qn-1=54,从而(q-1)qn-1=qn-qn-1=54。
∴qn-1=81-54=27
∴q=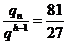 =3。
=3。
∴a1=q-1=2
故此数列的首为2,公比为3。
(2)解法1:设插入的n个数为 ,且公比为q,
,且公比为q,
则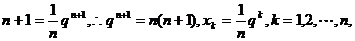
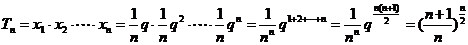 。
。
解法2:设插入的n个数为 ,
,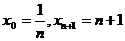
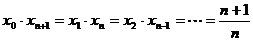
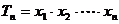
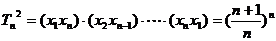
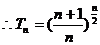 。
。
(3)解法一 设公比为q,项数为2m,m∈N*,
设公比为q,项数为2m,m∈N*,
依题意有: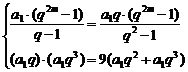 ,
,
化简得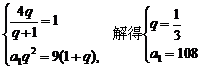 ,
,
设数列{lgan}前n项和为Sn,
则Sn=lga1+lga1q2+…+lga1qn-1=lga1n·q1+2+…+(n-1)
=nlga1+ n(n-1)·lgq=n(2lg2+lg3)-
n(n-1)·lgq=n(2lg2+lg3)- n(n-1)lg3
n(n-1)lg3
=(-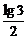 )·n2+(2lg2+
)·n2+(2lg2+ lg3)·n
lg3)·n
可见,当n=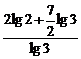 时,Sn最大,
时,Sn最大,
而 =5,故{lgan}的前5项和最大,
=5,故{lgan}的前5项和最大,
解法二 接前,
接前, ,于是lgan=lg[108(
,于是lgan=lg[108( )n-1]=lg108+(n-1)lg
)n-1]=lg108+(n-1)lg ,
,
∴数列{lgan}是以lg108为首项,以lg 为公差的等差数列,
为公差的等差数列,
令lgan≥0,得2lg2-(n-4)lg3≥0,
∴n≤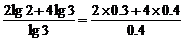 =5.5,
=5.5,
由于n∈N*,可见数列{lgan}的前5项和最大。
点评:第一种解法利用等比数列的基本量 ,先求公比,后求其它量,这是解等差数列、等比数列的常用方法,其优点是思路简单、实用,缺点是有时计算较繁;第二种解法利用等比数列的性质,与“首末项等距”的两项积相等,这在解题中常用到。
,先求公比,后求其它量,这是解等差数列、等比数列的常用方法,其优点是思路简单、实用,缺点是有时计算较繁;第二种解法利用等比数列的性质,与“首末项等距”的两项积相等,这在解题中常用到。
题型6:等差、等比综合问题
例11.(2006年广东卷)已知公比为 的无穷等比数列
的无穷等比数列 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列 各项的和为
各项的和为 。
。
(Ⅰ)求数列 的首项
的首项 和公比
和公比 ;
;
(Ⅱ)对给定的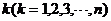 ,设
,设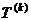 是首项为
是首项为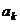 ,公差为
,公差为 的等差数列.求数列
的等差数列.求数列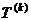 的前10项之和。
的前10项之和。
解析:(Ⅰ)依题意可知: ,
,
(Ⅱ)由(Ⅰ)知,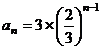 ,所以数列
,所以数列 的的首项为
的的首项为 ,公差
,公差 ,
,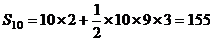 ,即数列
,即数列 的前10项之和为155。
的前10项之和为155。
点评:对于出现等差、等比数列的综合问题,一定要区分开各自的公式,不要混淆。
4.等比数列前n项和公式
一般地,设等比数列 的前n项和是
的前n项和是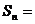
 ,当
,当 时,
时, 或
或 ;当q=1时,
;当q=1时, (错位相减法)。
(错位相减法)。
说明:(1) 和
和 各已知三个可求第四个;(2)注意求和公式中是
各已知三个可求第四个;(2)注意求和公式中是 ,通项公式中是
,通项公式中是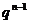 不要混淆;(3)应用求和公式时
不要混淆;(3)应用求和公式时 ,必要时应讨论
,必要时应讨论 的情况。
的情况。
3.等比中项
如果在 中间插入一个数
中间插入一个数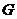 ,使
,使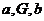 成等比数列,那么
成等比数列,那么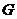 叫做
叫做 的等比中项(两个符号相同的非零实数,都有两个等比中项)。
的等比中项(两个符号相同的非零实数,都有两个等比中项)。
2.等比数列通项公式为: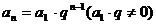 。
。
说明:(1)由等比数列的通项公式可以知道:当公比 时该数列既是等比数列也是等差数列;(2)等比数列的通项公式知:若
时该数列既是等比数列也是等差数列;(2)等比数列的通项公式知:若 为等比数列,则
为等比数列,则 。
。
1.等比数列定义
一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比;公比通常用字母 表示
表示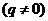 ,即:
,即: :
: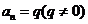 数列对于数列(1)(2)(3)都是等比数列,它们的公比依次是2,5,
数列对于数列(1)(2)(3)都是等比数列,它们的公比依次是2,5, 。(注意:“从第二项起”、“常数”
。(注意:“从第二项起”、“常数” 、等比数列的公比和项都不为零)
、等比数列的公比和项都不为零)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com