2.关于一定历史时期人地关系的叙述，正确的是(　)　

A.采猎文明时期，人受地的制约比较小　

B.农业革命以后，人地关系得到和谐发展　

C.产业革命之后，人地关系开始出现矛盾，局部地区产生环境问题　

D.到了近代，人们对人地关系的认识逐渐走向系统化和科学化　

1.关于农业文明时期人地关系的叙述，正确的是(　)　

①人与自然的对抗性增强，地理环境遭到破坏　

②人类对人地关系的认识有了科学的萌芽　

③环境对人类的制约作用较强，人类改造环境的作用微弱　

④大规模的耕作、灌溉和放牧使生态系统日趋复杂和稳定　

A.①②　　　　　　 B.③④　　　　　 C.①③　　　　　 D.②④　

10．( 2005福建)如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

(Ⅰ)求证AE⊥平面BCE；

(Ⅱ)求二面角B-AC-E的大小；

(Ⅲ)求点D到平面ACE的距离.

分析：本小题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识，考查空间想象能力，逻辑思维能力与运算能力.

解法一：

(Ⅰ)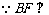平面ACE.　 .

∵二面角D-AB-E为直二面角，且， 平面ABE.

(Ⅱ)连结BD交AC于C，连结FG，

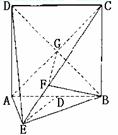
∵正方形ABCD边长为2，

∴BG⊥AC，BG=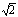，平面ACE，

由三垂线定理的逆定理得FG⊥AC.

是二面角B-AC-E的平面角.

由(Ⅰ)AE⊥平面BCE， 又，

∴在等腰直角三角形AEB中，BE=.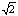

又直角

，

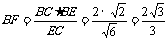∴二面角B-AC-E等于

(Ⅲ)过点E作交AB于点O. OE=1.

∵二面角D-AB-E为直二面角，∴EO⊥平面ABCD.

设D到平面ACE的距离为h，

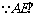平面BCE，

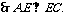
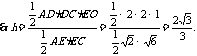
∴点D到平面ACE的距离为

9．(2004天津) 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F.

(Ⅰ)证明PA//平面EDB；

(Ⅱ)证明PB⊥平面EFD；

(Ⅲ)求二面角C-PB-D的大小.　　　　　

(1)证明：连结AC，AC交BD于O，连结EO.

∵底面ABCD是正方形，

∴点O是AC的中点

在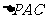中，EO是中位线，∴PA // EO

而平面EDB且平面EDB，

所以，PA // 平面EDB

(2)证明：∵PD⊥底面ABCD且底面ABCD，

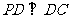∴　 ∵PD=DC，可知是等腰直角三角形，而DE是斜边PC的中线，

∴.　　　　　　　 　　　　　①

同样由PD⊥底面ABCD，得PD⊥BC.

∵底面ABCD是正方形，有DC⊥BC，

∴BC⊥平面PDC.

而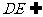平面PDC，∴.　　 ②

由①和②推得平面PBC.

而平面PBC，∴

又且，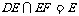

所以PB⊥平面EFD.

(3)解：由(2)知，，故是二面角C-PB-D的平面角.

由(2)知，.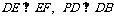

设正方形ABCD的边长为a，则

,

，

，.

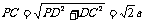在中，

.

在中，

,

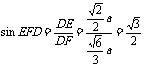∴，二面角C-PB-D的大小为.

8．已知矩形ABCD中,AB=1, BC=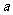(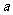>0),PA⊥面ABCD,PA=1

(1)问BC边上是否存在一点Q，使得PQ⊥QD并且说明理由

(2)若BC边上有且只有一个点Q使得PQ⊥QD，求这时二面角Q-PD-A大小

解：(1) a=2时只有一点；a＞2时有两点；a＜2时没有点；

(2)arctan

7．在直三棱柱ABC-A₁B₁C₁中，底面三角形ABC为等腰直角三角形，且∠ABC=90^ο ，E为C₁C的中点 ，F

是BB₁上是BF=BB₁，AC=AA₁=2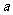,求平面EFA与面ABC所成角的大小

答案： arctan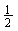

5. 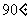;　　　　　　 6.[0°，90°]；

提示:3. l⊥平面PAB于C,PC是ΔPAB外接圆直径，用余、正弦定理.

[解答题]

6．一条直线与直二面角的两个面所成的角分别是α和β，则α+β的范围是_____．

◆答案提示：　 1-3. BCB;　　 4. a⊥b;

5．(2005浙江)设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E(如图)．现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于_________．

4.设a、b是异面直线，α、β是两个平面，且a⊥α，b⊥β，aβ，bα，则当_______(填上一种条件即可)时，有α⊥β.