3．人耳可以听到的声波的频率范围是20Hz-20000Hz。频率低于20Hz的声波叫次声波，频率高于20000Hz的声波叫超声波。

2．空气中的声速可认为是340m/s，水中的声速是1450m/s，铁中的声速是5400m/s。

1．空气中的声波是纵波。

7．波动图象的应用：

(1)从图象上直接读出振幅、波长、任一质点在该时刻的振动位移。

(2)波动方向<==>振动方向。

方法：选择对应的半周，再由波动方向与振动方向“头头相对、尾尾相对”来判断。

如图：

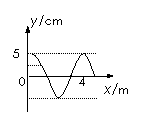[例7]如图是一列沿x轴正方向传播的机械波在某时刻的波

形图。由图可知：这列波的振幅为5cm，波长为 4m 。此时刻

P点的位移为2.5cm，速度方向为沿y轴正方向，加速度方向

沿y轴负方向； Q点的位移为－5cm，速度为　 0 ，加速度方

向沿y轴正方向。

[例8]如图是一列波在t₁=0时刻的波形，波的传播速度

为2m/s，若传播方向沿x轴负向，则从t₁=0到t₂=2.5s的时间

内，质点M通过的路程为______，位移为_____。　　　　　　　　　　

解析：由图：波长λ=0.4m，又波速v=2m/s，可得：

周期T=0.2s，所以质点M振动了12.5T。

对于简谐振动，质点振动1T，通过的路程总是4A；振动0.5T，通过的路程总是2A。

所以，质点M通过的路程12×4A+2A=250cm=2.5m。质点M振动12.5T时仍在平衡位置。

所以位移为0。

[例9]在波的传播方向上，距离一定的P与Q点之间只有一个波谷的四种情况，如图A、B、C、D所示。已知这四列波在同一种介质中均向右传播，则质点P能首先达到波谷的是( 　)

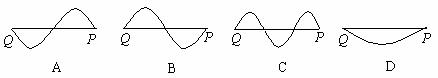
解析：四列波在同一种介质中传播，则波速v应相同。由T=λ/v得：T_D>T_A=T_B>T_C；

再结合波动方向和振动方向的关系得：C图中的P点首先达到波谷。

(3)两个时刻的波形问题：设质点的振动时间(波的传播时间)为t，波传播的距离为x。

则：t=nT+△t即有x=nλ+△x (△x=v△t) 且质点振动nT(波传播nλ)时，波形不变。

①根据某时刻的波形，画另一时刻的波形。

方法1：波形平移法：当波传播距离x=nλ+△x时，波形平移△x即可。

方法2：特殊质点振动法：当波传播时间t=nT+△t时，根据振动方向判断相邻特殊点(峰点，谷点，平衡点)振动△t后的位置进而确定波形。

②根据两时刻的波形，求某些物理量(周期、波速、传播方向等)

[例10]如图是一列向右传播的简谐横波在某时刻的波形图。

已知波速v=0.5m/s，画出该时刻7s前及7s后的瞬时波形图。

解析：λ=2m，v=0.5m/s，T =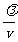=4 s.所以⑴波在7s内传播

的距离为x=vt=3.5m=1λ⑵质点振动时间为1T。

方法1　 波形平移法：现有波形向右平移λ可得7s后的波形；

现有波形向左平移λ可得7s前的波形。

由上得到图中7s后的瞬时波形图(粗实线)和7s前的瞬时波形图(虚线)。

方法2　 特殊质点振动法：根据波动方向和振动方向的关系，确定两个特殊点(如平衡点和峰点)在3T/4前和3T/4后的位置进而确定波形。请读者试着自行分析画出波形。

[例11]如图实线是某时刻的波形图象，虚线是经过0.2s

时的波形图象。求：

①波传播的可能距离 ②可能的周期(频率)

③可能的波速　 ④若波速是35m/s，求波的传播方向　

⑤若0.2s小于一个周期时，传播的距离、周期(频率)、波速。

解析：

①题中没给出波的传播方向，所以有两种可能：向左传播或向右传播。

向左传播时，传播的距离为x=nλ+3λ/4=(4n+3)m　 (n=0、1、2　 …)

向右传播时，传播的距离为x=nλ+λ/4=(4n+1)m　 (n=0、1、2　 …)

②向左传播时，传播的时间为t=nT+3T/4得：T=4t/(4n+3)=0.8 /(4n+3)(n=0、1、2　 …)

向右传播时，传播的时间为t=nT+T/4得：T=4t/(4n+1)=0.8 /(4n+1)　 (n=0、1、2　 …)

③计算波速，有两种方法。v=x/t 　或v=λ/T

向左传播时，v=x/t=(4n+3)/0.2=(20n+15)m/s. 或v=λ/T=4 (4n+3)/0.8=(20n+15)m/s.(n=0、1、2　 …)

向右传播时，v=x/t=(4n+1)/0.2=(20n+5)m/s. 或v=λ/T=4 (4n+1)/0.8=(20n+5)m/s. (n=0、1、2　 …)

④若波速是35m/s，则波在0.2s内传播的距离为x=vt=35×0.2m=7m=1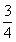λ，所以波向左传播。

⑤若0.2s小于一个周期，说明波在0.2s内传播的距离小于一个波长。则：

向左传播时，传播的距离x=3λ/4=3m；传播的时间t=3T/4得：周期T=0.267s；波速v=15m/s.向右传播时，传播的距离为λ/4=1m；传播的时间t=T/4得：周期T=0.8s；波速v =5m/s.

点评：做此类问题的选择题时，可用答案代入检验法。

(4)根据波的传播特点(运动状态向后传)确定某质点的运动状态问题：

[例12]一列波在介质中向某一方向传播，如图是此波在某一时刻的波形图，且此时振动还只发生在M、N之间，并知此波的周期为T，Q质点速度方向在波形中是向下的。则：波源是_____；P质点的起振方向为_________；从波源起振开始计时时，P点已经振动的时间为______。

解析：由Q点的振动方向可知波向左传播，N是波源。

由M点的起振方向(向上)得P质点的起振方向向上。振动从N点传播到M点需要1T，传播到P点需要3T/4，所以质点P已经振动的时间为T/4.

[例13]如图是一列向右传播的简谐横波在t=0时刻(开始计时)的波形图，已知在t=1s时，B点第三次达到波峰(在1s内B点有三次达到波峰)。则：

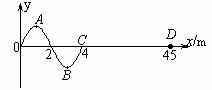
①周期为________　　　　　　 ②波速为______；

③D点起振的方向为_________；④在t=____s时刻，此波传到D点；在t=____s和t=___s时D点分别首次达到波峰和波谷；在t=____s和t=___s时D点分别第二次达到波峰和波谷。

解析：

①B点从t=0时刻开始在经过t=2.5T=1s第三次达到波峰，故周期T=0.4s.　

②由v=λ/T=10m/s.　

③D点的起振方向与介质中各质点的起振方向相同。在图示时刻，C点恰好开始起振，由波动方向可知C点起振方向向下。所以，D点起振方向也是向下。

④从图示状态开始计时：此波传到D点需要的时间等于波从C点传播到D需要的时间，即：t=(45－4)/10=4.1s；　 D点首次达到波峰的时间等于A质点的振动状态传到D点需要的时间，即：t=(45－1) /10=4.4s； D点首次达到波谷的时间等于B质点的振动状态传到D点需要的时间，即：t=(45－3)/10=4.2s；D点第二次达到波峰的时间等于D点首次达到波峰的时间再加上一个周期，即：t=4.4 s+0.4s=4.8 s.　 D点第二次达到波谷的时间等于D点首次达到波峰的时间再加上一个周期，即：t=4.2s+0.4s=4.6s.

[例14]　 已知在t₁时刻简谐横波的波形如图中实线所示；在时刻t₂该波的波形如图中虚线所示。t₂-t₁ = 0.02s。求：

(1)该波可能的传播速度。

(2)若已知T< t₂-t₁<2T，且图中P质点在t₁时刻的瞬时速度方向向上，求可能的波速。

(3)若0.01s<T<0.02s，且从t₁时刻起，图中Q质点比R质点先回到平衡位置，求可能的波速。

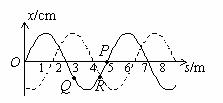
解析：(1)如果这列简谐横波是向右传播的，在t₂-t₁内波形向右匀速传播了，所以波速=100(3n+1)m/s (n=0，1，2，…)；同理可得若该波是向左传播的，可能的波速v=100(3n+2)m/s　 (n=0，1，2，…)

(2)P质点速度向上，说明波向左传播，T< t₂-t₁ <2T，说明这段时间内波只可能是向左传播了5/3个波长，所以速度是唯一的：v=500m/s

(3)“Q比R先回到平衡位置”，说明波只能是向右传播的，而0.01s<T<0.02s，也就是T<0.02s<2T，所以这段时间内波只可能向右传播了4/3个波长，解也是唯一的：v=400m/s

6．起振方向

介质中每个质点开始振动的方向都和振源开始振动的方向相同。

[例5] 在均匀介质中有一个振源S，它以50H_Z的频率上下振动，该振动以40m/s的速度沿弹性绳向左、右两边传播。开始时刻S的速度方向向下，试画出在t=0.03s时刻的波形。

解析：从开始计时到t=0.03s经历了1.5个周期，波分别向左、右传播1.5个波长，该时刻波源S的速度方向向上，所以波形如右图所示。

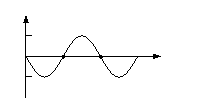[例6] 如图所示是一列简谐横波在t=0时刻的波形图，已知这列波沿x轴正方向传播，波速为20m/s。P是离原点为2m的一个介质质点，则在t=0.17s时刻，质点P的：①速度和加速度都沿-y方向；②速度沿+y方向，加速度沿-y方向；③速度和加速度都正在增大；④速度正在增大，加速度正在减小。

以上四种判断中正确的是

A．只有①　　　　　　 B．只有④

C．只有①④　　　　　 D．只有②③

解析：由已知，该波的波长λ=4m，波速v=20m/s，因此周期为T=λ/v=0.2s；因为波向右传播，所以t=0时刻P质点振动方向向下；0.75 T <0.17s< T，所以P质点在其平衡位置上方，正在向平衡位置运动，位移为正，正在减小；速度为负，正在增大；加速度为负，正在减小。①④正确，选C

5．介质质点的运动是简谐运动(是一种变加速运动)

任何一个介质质点在一个周期内经过的路程都是4A，在半个周期内经过的路程都是2A，但在四分之一个周期内经过的路程就不一定是A了。

4．波的传播是匀速的

在一个周期内，波形匀速向前推进一个波长。n个周期波形向前推进n个波长(n可以是任意正数)。因此在计算中既可以使用v=λžf，也可以使用v=s/t，后者往往更方便。

3．波的图象的画法

波的图象中，波的图形、波的传播方向、某一介质质点的瞬时速度方向，这三者中已知任意两者，可以判定另一个。(口诀为“上坡下，下坡上” ；或者“右上右、左上左))

2．描述波的物理量--波速、周期、波长：

(1)波速v：运动状态或波形在介质中传播的速率；同一种波的波速由介质决定。

注：在横波中，某一波峰(波谷)在单位时间内传播的距离等于波速。

(2)周期T：即质点的振动周期；由波源决定。

(3)波长λ：在波动中，振动位移总是相同的两个相邻质点间的距离。

注：在横波中，两个相邻波峰(波谷)之间的距离为一个波长。

结论：

(1)波在一个周期内传播的距离恰好为波长。

由此：①v=λ/T=λf；λ=vT.　　 ②波长由波源和介质决定。

(2)质点振动nT(波传播nλ)时，波形不变。

(3)相隔波长整数倍的两质点，振动状态总相同；相隔半波长奇数倍的两质点，振动状态总相反。

1．振动图象和波的图象

振动图象和波的图象从图形上看好象没有什么区别，但实际上它们有本质的区别。

(1)物理意义不同：振动图象表示同一质点在不同时刻的位移；波的图象表示介质中的各个质点在同一时刻的位移。 　　　　　　　　　　　　　　　

(2)图象的横坐标的单位不同：振动图象的横坐标表示时间；波的图象的横坐标表示距离。

(3)从振动图象上可以读出振幅和周期；从波的图象上可以读出振幅和波长。

简谐振动图象与简谐横波图象的列表比较：

	简谐振动	简谐横波
图 象
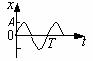坐 标	横坐标	时间	介质中各质点的平衡位置
纵坐标	质点的振动位移	各质点在同一时刻的振动位移
研究对象	一个质点	介质中的大量质点
物理意义	一个质点在不同时刻的振动位移	介质中各质点在同一时刻的振动位移
随时间的变化	原有图形不变，图线随时间而延伸	原有波形沿波的传播方向平移
运动情况	质点做简谐运动	波在介质中匀速传播；介质中各质点做简谐振动