3.电磁感应中的能量守恒

只要有感应电流产生，电磁感应现象中总伴随着能量的转化。电磁感应的题目往往与能量守恒的知识相结合。这种综合是很重要的。要牢固树立起能量守恒的思想。

[例5] 如图所示，矩形线圈abcd质量为m，宽为d，在竖直平面内由静止自由下落。其下方有如图方向的匀强磁场，磁场上、下边界水平，宽度也为d，线圈ab边刚进入磁场就开始做匀速运动，那么在线圈穿越磁场的全过程，产生了多少电热？

解：ab刚进入磁场就做匀速运动，说明安培力与重力刚好平衡，在下落2d的过程中，重力势能全部转化为电能，电能又全部转化为电热，所以产生电热Q =2mgd。

[例6]如图所示，水平面上固定有平行导轨，磁感应强度为B的匀强磁场方向竖直向下。同种合金做的导体棒ab、cd横截面积之比为2∶1，长度和导轨的宽均为L，ab的质量为m ，电阻为r，开始时ab、cd都垂直于导轨静止，不计摩擦。给ab一个向右的瞬时冲量I，在以后的运动中，cd的最大速度v_m、最大加速度a_m、产生的电热各是多少？

解：给ab冲量后，ab获得速度向右运动，回路中产生感应电流，cd受安培力作用而加速，ab受安培力而减速；当两者速度相等时，都开始做匀速运动。所以开始时cd的加速度最大，最终cd的速度最大。全过程系统动能的损失都转化为电能，电能又转化为内能。由于ab、cd横截面积之比为2∶1，所以电阻之比为1∶2，根据Q=I ²Rt∝R，所以cd上产生的电热应该是回路中产生的全部电热的2/3。又根据已知得ab的初速度为v₁=I/m，因此有： ，解得。最后的共同速度为v_m=2I/3m，系统动能损失为ΔE_K=I ²/ 6m，其中cd上产生电热Q=I ²/ 9m

2.转动产生的感应电动势

⑴转动轴与磁感线平行。如图磁感应强度为B的匀强磁场方向垂直于纸面向外，长L的金属棒oa以o为轴在该平面内以角速度ω逆时针匀速转动。求金属棒中的感应电动势。在用导线切割磁感线产生感应电动势的公式时注意其中的速度v应该是平均速度，即金属棒中点的速度。

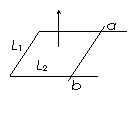
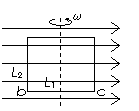⑵线圈的转动轴与磁感线垂直。如图矩形线圈的长、宽分别为L₁、L₂，所围面积为S，向右的匀强磁场的磁感应强度为B，线圈绕图示的轴以角速度ω匀速转动。线圈的ab、cd两边切割磁感线，产生的感应电动势相加可得E=BSω。如果线圈由n匝导线绕制而成，则E=nBSω。从图示位置开始计时，则感应电动势的即时值为e=nBSωcosωt 。该结论与线圈的形状和转动轴的具体位置无关(但是轴必须与B垂直)。

实际上，这就是交流发电机发出的交流电的即时电动势公式。

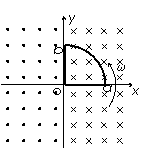
[例4] 如图所示，xoy坐标系y轴左侧和右侧分别有垂直于纸面向外、向里的匀强磁场，磁感应强度均为B，一个围成四分之一圆形的导体环oab，其圆心在原点o，半径为R，开始时在第一象限。从t=0起绕o点以角速度ω逆时针匀速转动。试画出环内感应电动势E随时间t而变的函数图象(以顺时针电动势为正)。

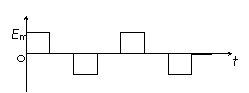解：开始的四分之一周期内，oa、ob中的感应电动势方向相同，大小应相加；第二个四分之一周期内穿过线圈的磁通量不变，因此感应电动势为零；第三个四分之一周期内感应电动势与第一个四分之一周期内大小相同而方向相反；第四个四分之一周期内感应电动势又为零。感应电动势的最大值为E_m=BR²ω，周期为T=2π/ω，图象如右。

1.法拉第电磁感应定律

电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比，即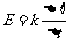，在国际单位制中可以证明其中的k=1，所以有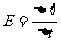。对于n匝线圈有。

在导线切割磁感线产生感应电动势的情况下，由法拉第电磁感应定律可推出感应电动势的大小是：E=BLvsinα(α是B与v之间的夹角)。

[例1]如图所示，长L₁宽L₂的矩形线圈电阻为R，处于磁感应强度为B的匀强磁场边缘，线圈与磁感线垂直。求：将线圈以向右的速度v匀速拉出磁场的过程中，⑴拉力F大小； ⑵拉力的功率P； ⑶拉力做的功W； ⑷线圈中产生的电热Q ；⑸通过线圈某一截面的电荷量q 。

解：这是一道基本练习题，要注意要注意所用的边长究竟是L₁还是L₂ ，还应该思考一下所求的各物理量与速度v之间有什么关系。

⑴

⑵

⑶

⑷

⑸ 与v无关

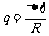特别要注意电热Q和电荷q的区别，其中与速度无关！(这个结论以后经常会遇到)。

[例2]如图所示，竖直放置的U形导轨宽为L，上端串有电阻R(其余导体部分的电阻都忽略不计)。磁感应强度为B的匀强磁场方向垂直于纸面向外。金属棒ab的质量为m，与导轨接触良好，不计摩擦。从静止释放后ab保持水平而下滑。试求ab下滑的最大速度v_m

解：释放瞬间ab只受重力，开始向下加速运动。随着速度的增大，感应电动势E、感应电流I、安培力F都随之增大，加速度随之减小。当F增大到F=mg时，加速度变为零，这时ab达到最大速度。

　　 由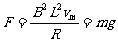，可得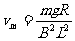

点评：这道题也是一个典型的习题。要注意该过程中的功能关系：重力做功的过程是重力势能向动能和电能转化的过程；安培力做功的过程是机械能向电能转化的过程；合外力(重力和安培力)做功的过程是动能增加的过程；电流做功的过程是电能向内能转化的过程。达到稳定速度后，重力势能的减小全部转化为电能，电流做功又使电能全部转化为内能。这时重力的功率等于电功率也等于热功率。

进一步讨论：如果在该图上端电阻右边安一只电键，让ab下落一段距离后再闭合电键，那么闭合电键后ab的运动情况又将如何？(无论何时闭合电键，ab可能先加速后匀速，也可能先减速后匀速，但最终稳定后的速度总是一样的)。

[例3] 如图所示，U形导线框固定在水平面上，右端放有质量为m的金属棒ab，ab与导轨间的动摩擦因数为μ，它们围成的矩形边长分别为L₁、L₂，回路的总电阻为R。从t=0时刻起，在竖直向上方向加一个随时间均匀变化的匀强磁场B=kt，(k>0)那么在t为多大时，金属棒开始移动？

解：由= kL₁L₂可知，回路中感应电动势是恒定的，电流大小也是恒定的，但由于安培力F=BIL∝B=kt∝t，随时间的增大，安培力将随之增大。当安培力增大到等于最大静摩擦力时，ab将开始向左移动。这时有：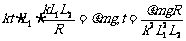

例7. 利用如图所示的一只电压表、一个电阻箱和一个电键，测量一个电池组的电动势和内电阻。请画出实验电路图，并用笔画线作导线将所给器材连接成实验电路。用记录的实验数据写出电动势和内电阻的表达式。

解：与学生实验相比，用电阻箱代替了电流表。由于电压可测，由电压、电阻就可以算出电流(这个电流是通过电阻箱的电流，比通过电池的电流偏小，系统误差是由电压表的分流造成的)。电路图如下。实验步骤是：

　 (1) 按电路图接好实验电路

(2)改变电阻箱阻值，分别读出两组电阻箱阻值和对应的路端电压值R₁、U₁、R₂、U₂。

(3)根据闭合电路欧姆定律列出与这两组数据相对应的方程：

。

⑷解方程组可得E和r：

如果只给出电阻箱和电流表，用类似的方法同样可以测量电源的电动势和内电阻。

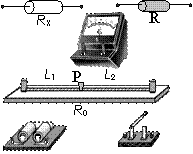
例8. 电桥法测电阻。利用给出的电路图和器材(G为灵敏电流表，R₀为阻值均匀的电阻丝，R为已知阻值的定值电阻，R_x为被测电阻)。要求利用这些器材测未知电阻R_x。(1)实验中还需要什么测量仪器？

(2)将实物连成电路图。

(3)写出测量R_x的实验步骤，并写出利用测量数据表示R_x的表达式。

解：

(1)还需要米尺(测量左右两部分电阻丝的长度L₁、L₂)。

(2)实物连接图略。

(3)按图接好电路后，移动滑动触头P，使电流表指针指在中央零刻度处。用刻度尺测量P点两边电阻丝的长度L₁、L₂；由R_X∶R=L₁∶L₂得。

例9. 下右图中的P是一根表面均匀地镀有一层很薄的电阻膜的长陶瓷管(碳膜布满圆柱体的外侧面)。陶瓷管的长度约为50cm，外径约为6cm，所用电阻膜材料的电阻率已知为ρ，管的两端有导电箍M、N。该电阻的长度就是陶瓷管的长度，其截面积可看作等于膜的厚度与圆周长的乘积。现有器材为：A.米尺、B.游标卡尺、C.螺旋测微器、D.电压表、E.电流表、F.电池组、G.滑动变阻器、H.电阻箱、I.电键和导线。请你设计一个测量该电阻膜厚度d的实验方案。

　 　(1)所须选用的器材有：__________________(填器材前的字母即可)。

　 　(2)所须测量的物理量有：_____ 、_____、 _____、 _____。

　 (3)根据实验测得的以上数据计算电阻膜厚度d的数学表达式为：d=________________。

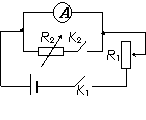
　 (4)在左下图的方框中画出实验电路图(MN间的电阻膜的电阻约几个kΩ，滑动变阻器的总阻值为50Ω)。并将右下图中的实物按电路图连接起来(有3根导线已经连好，不得改动)。

解：

(1)A(用来测量MN间的长度)、B(用来测量陶瓷管的外径)、D、E、F、G、I(以上用来测量电阻膜的阻值)

　(2)MN间距离L、管的外径D、电流I、电压U

　(3)

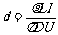
(4)测量大电阻所以要采用电流表内接法；由于被测电阻阻值　 远大于滑 动变阻器的总阻值，所以只有采用分压电路才能做到多取几组数据测电阻值，减小偶然误差。

例10. 在实验室中，往往利用半偏法测量电流表或电压表的内阻。测量电路图如右。E为电源，其电动势为E。R₁为总阻值较大的滑动变阻器。R₂为电阻箱。A为被测电流表。用此电路，经以下步骤可近似测得电流表的内阻R_A：①闭合K₁，断开K₂，调节R₁，使电流表读数等于其量程I₀；②保持R₁不变，闭合K₂，调节R₂，使电流表读数等于I₀/2；③读出R₂的值，则R_A=R₂。

(1)按照电路图在右边实物图所给出的实物图中画出连接导线。

(2)若电源的内阻忽略不计，试分析该实验的系统误差总是使电表内阻的测量值比其真实值偏大还是偏小？

解：

(1)图略。

(2)闭合K₂后，回路的总电阻减小，总电流将增大。因此当电流表读数等于I₀/2时，通过电阻箱的电流将略大于I₀/2，实际上电阻箱的电阻比表头电阻小一些，也就是说测量值比真实值偏小。

例11. 用伏安法测电阻时，由于电压表、电流表内阻的影响，测量结果总存在系统误差。按下图所示的电路进行测量，可以消除这种系统误差。

(1)该实验的第一步是：闭合电键S₁，将电键S₂接2，调节滑动变阻器R_P和r，使电压表读数尽量接近满量程，读出这时电压表和电流表的示数U₁、I₁；请你接着写出第二步，并说明需要记录的数据：_________________________。

(2)由以上记录数据计算被测电阻R_X的表达式是R_X=___________。

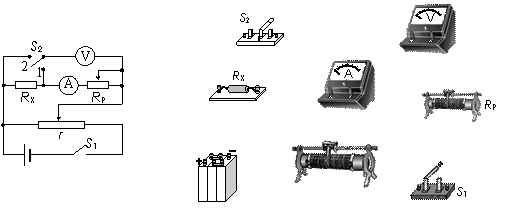(3)将右图中给出的仪器按照电路图的要求连接起来。

解：

(1)将电键S₂接1，读出这时电压表和电流表的示数U₂、I₂。

(2)

　(3)图略。

例12. 某同学选用一只标有“3.8V 0.3A”的小灯泡，用电流表和电压表测量它在不同电压下的电流，从而计算出它在不同电压下的实际电阻值。根据实验数据画出的I-U图象如右。

(1)从图象看出，电压越高对应的实际电阻值越_____，这说明灯丝材料的电阻率随温度的升高而________。

(2)若实验室提供的器材是：电动势为6V，内阻很小的铅蓄电池；量程0-0.6-3A的直流电流表；量程0-3-15V的直流电压表；最大阻值10Ω的滑动变阻器；一只电键和若干导线。请画出正确的实验电路图。并标出开始实验时所用的电表量程和滑动变阻器滑动触头的位置。

解：

(1)曲线上每一点和原点的连线的斜率的倒数表示该时刻对应的灯丝电阻。由图象可知随着电压的升高灯丝的电阻增大。这说明灯丝材料的电阻率随温度的升高而增大。

(2)正常工作时灯丝的电阻才十几个欧姆，电压低时电阻更小，所以应作为小电阻处理，测量部分应该用外接法。灯丝两端的电压要求从零开始逐渐增大，所以供电部分必须采用分压电路。开始时电流表量程应选用0.6A，电压表量程应选用3V(快要超过3V时再改用15V量程)，滑动变阻器滑动触头的位置应使灯丝两端分到的电压为零。

例13. 随着居民生活水平的提高，纯净水已经进入千家万户。某市对市场上出售的纯净水质量进行了抽测，结果发现竞有九成样品的细菌超标或电导率不合格(电导率是电阻率的倒数，是检验纯净水是否合格的一项重要指标)。(1)不合格的纯净水的电导率一定是偏_____(填大或小)。

(2)对纯净水样品进行检验所用的设备原理如图所示，将采集的水样装入绝缘性能良好的塑料圆柱形容器内，容器两端用金属圆片电极密封。请把检测电路连接好(要求测量尽可能准确，已知水的电导率远小于金属的电导率，所用滑动变阻器的阻值较小)。

解：

(1)纯水的电阻率是很大的，因此电导率是很小的。不合格的纯净水一定是含有杂质，因此电导率偏大。

(2)测量部分用内接法，供电部分用分压电路。

2.研究电磁感应现象

首先要查明电流表指针偏转方向和电流方向的关系(方法与画电场中平面上等势线实验相同)。

电键闭合和断开时、电键闭合后滑动变阻器的滑动触头移动过程中、电键闭合后线圈A在B中插入、拔出时，都会发现电流表指针发生偏转，说明有感应电流产生。而电键保持闭合、滑动触头不动、线圈A 在B中不动时，电流表指针都不动，说明无感应电流产生。

结论：闭合电路中有感应电流产生的充分必要条件是穿过闭合电路的磁通量发生变化。

1.平行板电容器的电容

静电计是测量电势差的仪器。指针偏转角度越大，金属外壳和上方金属小球间的电势差越大。在本实验中，静电计指针和A板等电势，静电计金属壳和B板等电势，因此指针偏转角越大表示A、B两极板间的电压越高。

　　 本实验中，极板带电量保持不变。三个图依次表示：正对面积减小时电压增大；板间距离增大时电压增大；插入电介质时电压减小。由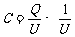知，这三种情况下电容分别减小、减小、增大。因此可以确定C和S、d、ε的关系是。

4.练习用多用电表测电阻

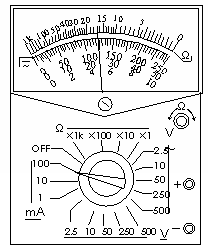(1)使用前应看一下指针是否指在刻度盘左端的零刻线处。如果不在，就应该进行机械调零：用小螺丝刀轻旋表头正下方中央处的调零螺丝，使指针指左端零刻线。

(2)根据被测物理量及其数量级将选择开关旋到相应的位置。读数时还要注意选用刻度盘上对应的量程刻度。(如测量20mA左右的直流电流，应将选择开关对准左边100mA量程处，在刻度盘上，应该看最下方的刻度，即满偏刻度为10的刻度线，从刻度盘读出数据后还应再乘10，得测量结果。)

(3)使用欧姆挡时，在选好倍率后，还必须进行欧姆调零。方法是：将红、黑表笔短接，调节欧姆调零旋钮，使指针指右端零刻线处。因此用多用电表的欧姆挡测电阻的操作步骤是：⑴选挡。一般比被测电阻的估计值低一个数量级，如估计值为200Ω就应该选×10的倍率。⑵进行欧姆调零。⑶将红黑表笔接被测电阻两端进行测量。

(4)将指针示数乘以倍率，得测量值。

(5)将选择开关扳到OFF或交流电压最高挡。

用欧姆挡测电阻，如果指针偏转角度太小(即指针所指的刻度值太大)，应该增大倍率重新调零后再测；如果指针偏转角度太大(即指针所指的刻度值太小)，应该减小倍率重新调零后再测。

(6)使用多用电表时，两只手只能握住表笔的绝缘棒部分，不能接触表笔上的金属部分。

例6. 多用电表表头的示意图如右。在正确操作的情况下：

(1)若选择开关的位置如灰箭头所示，则测量的物理量是______，测量结果为___________。

(2)若选择开关的位置如白箭头所示，则测量的物理量是______，测量结果为___________。

(3)若选择开关的位置如黑箭头所示，则测量的物理量是______，测量结果为___________。

(4)若选择开关的位置如黑箭头所示，正确操作后发现指针的偏转角很小，那么接下来的正确操作步骤应该依次为：___________，____________，____________。

(5)全部测量结束后，应将选择开关拨到__________或者___________。

(6)无论用多用电表进行何种测量(限于直流)，电流都应该从色_____表笔经______插孔流入电表。

解：

(1)直流电压，12.4V。

(2)直流电流，49mA。

(3)电阻，17kΩ。

(4)该用×1kΩ倍率，重新调零，将红黑表笔分别接触被测电阻的两根引线，读出指针所指刻度，再乘以倍率得测量值。

(5)OFF，交流电压500V档位置。

(6)红，正。

3.用电流表和电压表测电池的电动势和内电阻

实验电路如右。根据闭合电路欧姆定律：E=U+Ir，本实验电路中电压表的示数是准确的，而电流表的示数比通过电源的实际电流小，所以本实验的系统误差是由电压表的分流引起的。为了减小这个系统误差， 滑动变阻器R的阻值应该小一些，所选用的电压表的内阻应该大一些。

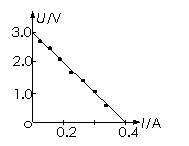为了减小偶然误差，要多做几次实验，多取几组数据，然后利用U-I图象处理实验数据。将点描好后，用直尺画一条直线，使尽可能多的点落在这条直线上，而且在直线两侧的点数大致相等。这条直线代表的U-I关系的偶然误差比每一组实验数据的偶然误差都小。这条直线在U轴上的截距就是被测电源电动势E(对应的I=0)，斜率的绝对值就是被测电源的内阻r。(特别要注意：有时纵坐标的起始点不是0，求内阻的一般式应该是r=|ΔU/ΔI |)。

例5. 在用电流表和电压表测电池的电动势和内电阻的实验中，所用的电流表和电压表的内阻分别约为0.1Ω和1kΩ。右边为实验原理图，下边为所需器材的实物图。试按原理图在实物图中画线连接成实验电路。

一位同学在实验中记录的6组数据如上表所示，试根据这些数据在右图中画出U-I图线。根据图线可读出被测电池的电动势E=____V，内电阻r=___Ω。

解：1.46，0.719

2.测定金属的电阻率

由于该实验中选用的被测电阻丝的电阻较小，所以测量电路应该选用伏安法中的电流表外接法。本实验对电压的调节范围没有特殊要求，被测电阻又较小，因此供电电路可以选用限流电路。

本实验通过的由于金属的电阻率随温度的升高而变大，因此实验中通电时间不能太长，电流也不宜太大，以免电阻丝发热后电阻率发生较明显的变化。由于选用限流电路，为保护电表和电源，闭合电键开始实验前应该注意滑动触头的位置，使滑动变阻器接入电路部分的电阻值最大。

例4. 在测定金属的电阻率的实验中，待测金属导线的长约0.8m，直径小于1mm，电阻在5Ω左右。实验主要步骤如下：⑴用______测量金属导线的长度l，测3次，求出平均值；⑵在金属导线的3个不同位置上用______________测量直径d，求出平均值；⑶用伏安法测量该金属导线的电阻R。在左边方框中画出实验电路图，并把右图中所给的器材连接成测量电路。安培计要求用0-0.6A量程，内阻约1Ω；伏特计要求用0-3V量程，内阻约几kΩ；电源电动势为6V；滑动变阻器最大阻值20Ω。在闭合电键前，滑动变阻器

的滑动触点应处于正确位置。 根据以上测量值，得到该种金属电阻率的表达式为ρ=__________。

解：

(1)米尺；

(2)螺旋测微器；

(3)测量部分用安培表外接法，电源部分用限流电路或分压电路都可以，电阻率 。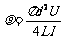

1.用描迹法画出电场中平面上的等势线

实验所用的电流表是零刻度在中央的灵敏电流表，在实验前应先查明电流方向与指针偏转方向的关系。方法是：将电流表、电池、电阻、导线按图a或图b 连接，若R是阻值很大的电阻，就按图a连接；若r是阻值很小的电阻，就按图b连接。然后用导线的a端试触电流表的另一端，观察电流表指针的偏转方向，就可判定电流方向和指针偏转方向的关系。

本实验是用恒定电流的电流场来模拟静电场。与电池正极相连的A电极相当于正点电荷，与电池负极相连的B相当于负点电荷。白纸应放在最下面，导电纸应放在最上面(涂有导电物质的一面必须向上)，复写纸则放在中间。

只要电流表示数是零，就表示两根探针针尖对应的点电势相等。把所有与同一个基准点电势相等的点连起来，就是等势线。

例3. 用恒定电流的电流场模拟静电场描绘等势线时，下列哪些模拟实验的设计是合理的

　　 ⑴　　　　⑵　　　　⑶　　　　 ⑷

　　 A.如图⑴所示圆柱形电极M、N都接电源的正极，模拟等量正点电荷周围的静电场

　　 B.如图⑵所示圆柱形电极M接电源正极，圆环形电极N接电源负极，模拟正点电荷周围附近的静电场

　　 C.如图⑶所示两个平行的长条形电极M、N分别接电源正、负极，模拟平行板电容器间的静电场

D.如图⑷所示圆柱形电极M接电源负极，模拟负点电荷周围的静电场

解：用电流场模拟静电场，在导电纸上必须形成电流。由于⑴、⑷两个方案在导电纸上不会形成电流，因此设计不合理。⑵、⑶两个设计是合理的。选BC。