2．极限分析法：常用此法分析圆周运动或平抛运动的临界状态。

1．等效法：有恒定的电场力参与的圆周运动，可以把重力与电场力的合力等效为新的重力mg′，新重力的方向即为合力的方向，据此确定圆周运动的等效最高点和最低点，类平抛运动的处理方法也属于等效法。

4．天体问题的处理方法：

(1)建立一种模型

在分析天体问题时，首先应把研究对象看作质点．这样，天体的运动就抽象为一个质点绕另一个质点的匀速圆周运动模型．

(2)抓住两条思路

①利用在中心天体表面或附近，万有引力近似等于重力， G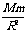=mg₀(g₀表示天体表面的重力加速度)。

②利用万有引力提供向心力。

　　 由此得到一个基本方程G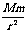=ma_加

3．竖直面内的圆周运动

　　 物体在竖直面内做圆周运动时，绝大多数属于变速圆周运动．在不同的约束条件下，物体能完成圆周运动的条件也是不同的．在绳(或沿圆环内侧运动)约束下，物体在最高点的速度v≥，在杆(管或弧形轨道外侧等)约束下，物体在最高点的速度v≥0．审题时一定要分清是绳模型还是杆模型，这是前提。

2．平抛运动分解为两个直线运动，两个直线沿什么方向与求解的问题有关，只要找出两个分运动的初速度和加速度，两个分运动就唯一的被确定了，然后按照直线运动的规律处理即可。

1．分运动与合运动是一种等效替代关系，其理论基础是运动的独立性原理，即任何一个运动可以看做是几个独立进行的分运动的合运动，其运算法则是平行四边形定则。分清合运动与分运动是解决问题的关键。物体相对于参考系的实际运动 (位移、速度)为合运动。

8.在磁感应强度为B=0.4 T的匀强磁场中放一个半径r₀=50 cm的圆形导轨，上面搁有互相垂直的两根导体棒，一起以角速度ω=10³ rad/s逆时针匀速转动.圆导轨边缘和两棒中央通过电刷与外电路连接，若每根导体棒的有效电阻为R₀=0.8 Ω，外接电阻R=3.9 Ω，如所示，求：

(1)每半根导体棒产生的感应电动势.

(2)当电键S接通和断开时两电表示数(假定R_V→∞，R_A→0).

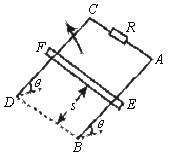
7.如图所示，AB和CD是足够长的平行光滑导轨，其间距为l，导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B的，方向垂直于导轨平面向上的匀强磁场中.AC端连有电阻值为R的电阻.若将一质量M，垂直于导轨的金属棒EF在距BD端s处由静止释放，在EF棒滑至底端前会有加速和匀速两个运动阶段.今用大小为F，方向沿斜面向上的恒力把EF棒从BD位置由静止推至距BD端s处，突然撤去恒力F，棒EF最后又回到BD端.求：

(1)EF棒下滑过程中的最大速度.　

(2)EF棒自BD端出发又回到BD端的整个过程中，有多少电能转化成了内能(金属棒、导轨的电阻均不计)?

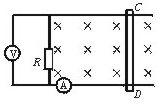
6.(1999年上海)如图所示，长为L、电阻r=0.3 Ω、质量m=0.1 kg的金属棒CD垂直跨搁在位于水平面上的两条平行光滑金属导轨上，两导轨间距也是L，棒与导轨间接触良好，导轨电阻不计，导轨左端接有R=0.5 Ω的电阻，量程为0-3.0 A的电流表串接在一条导轨上，量程为0-1.0 V的电压表接在电阻R的两端，垂直导轨平面的匀强磁场向下穿过平面.现以向右恒定外力F使金属棒右移.当金属棒以v=2 m/s的速度在导轨平面上匀速滑动时，观察到电路中的一个电表正好满偏，而另一个电表未满偏.问：

(1)此满偏的电表是什么表?说明理由.

(2)拉动金属棒的外力F多大?

(3)此时撤去外力F，金属棒将逐渐慢下来，最终停止在导轨上.求从撤去外力到金属棒停止运动的过程中通过电阻R的电量.

5.两根相距d=0.20 m的平行金属长导轨固定在同一水平面内，并处于竖直方向的匀强磁场中，磁场的磁感应强度B=0.20 T，导轨上面横放着两条金属细杆，构成矩形闭合回路.每条金属细杆的电阻为r=0.25 Ω，回路中其余部分的电阻可不计，已知两金属细杆在平行导轨的拉力作用下沿导轨朝相反方向匀速平移，速度大小都是v=5.0 m/s，如图所示，不计导轨上的摩擦.

(1)求作用于每条金属细杆的拉力的大小.

(2)求两金属细杆在间距增加0.40 m的滑动过程中共产生的热量.