
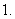 涉及等比数列的基本概念的问题,常用基本量
涉及等比数列的基本概念的问题,常用基本量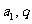 来处理;
来处理;
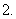 已知三个数成等比数列时,可设这三个数依次为
已知三个数成等比数列时,可设这三个数依次为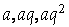 或
或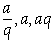 ;四个数时设为
;四个数时设为 、
、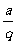 、
、 、
、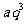
 等比数列的相关性质:
等比数列的相关性质:
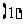 若
若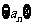 是等比数列,则
是等比数列,则 ;
;
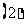 若
若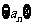 是等比数列,
是等比数列,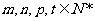 ,当
,当 时,
时,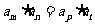
特别地,当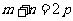 时,
时,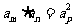
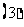 若
若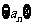 是等比数列,则下标成等差数列的子列构成等比数列;
是等比数列,则下标成等差数列的子列构成等比数列;
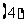 若
若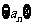 是等比数列,
是等比数列,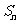 是
是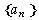 的前
的前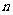 项和,则
项和,则 ,
, ,
,  …成等比数列.
…成等比数列.
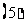 两个等比数列
两个等比数列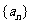 与
与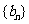 的积、商、倒数的数列
的积、商、倒数的数列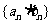 、
、 、
、 仍为等比数列.
仍为等比数列.
|
|
等差数列 |
等比数列 |
|
定义 |
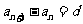 ( (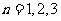 ,…) ,…) |
 ( (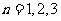 ,…) ,…) |
|
通项公式 |
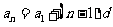 , ,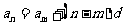 |
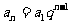 , ,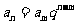 |
|
求和 公式 |
 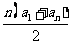 |
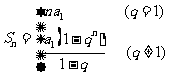 |
|
中项 公式 |
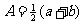 |
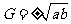 |
|
对称性 |
若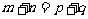 ,则 ,则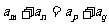 |
若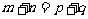 ,则 ,则 |
|
分段和原理 |
 、 、 、 、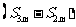 成等差数列 成等差数列 |
 、 、 、 、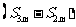 成等比数列 成等比数列 |
 等比数列的概念及其通项公式,等比数列前
等比数列的概念及其通项公式,等比数列前 项和公式;
项和公式;
 等比数列的有关性质;
等比数列的有关性质;
 等比数列的充要条件:
等比数列的充要条件:
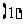
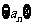 是等比数列
是等比数列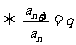 (
( 为非零常数);
为非零常数);
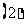
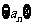 是等比数列
是等比数列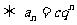 (
(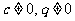 )
)
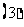
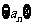 是等比数列
是等比数列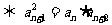
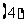
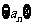 是等比数列
是等比数列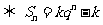 (
(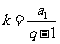 ,
,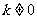 ,
,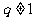 )
)
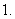 (
(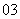 全国)等差数列
全国)等差数列 中,已知
中,已知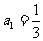 ,
,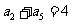 ,
,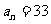 ,则
,则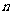 是
是
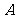




 (
( 春高考)设
春高考)设 (
(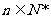 )是等差数列,
)是等差数列,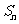 是前
是前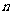 项和,
项和,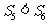 ,
,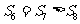 ,
,
则下列结论错误的是 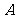
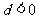

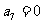

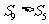

 与
与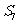 均为
均为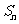 的最大项
的最大项
 (
( 福建文)设
福建文)设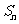 是等差数列
是等差数列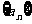 的前
的前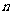 项和,若
项和,若 ,则
,则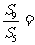
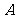
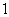




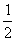
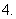 (
(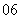 全国Ⅱ)设
全国Ⅱ)设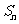 是等差数列
是等差数列 的前
的前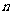 项和,若
项和,若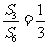 ,则
,则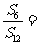

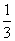

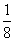

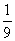
 (
( 福建)在等差数列
福建)在等差数列 中,已知
中,已知 则
则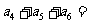

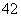

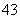

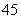
 (
(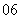 广东)已知等差数列共有
广东)已知等差数列共有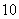 项,其中奇数项之和
项,其中奇数项之和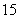 ,偶数项之和为
,偶数项之和为 ,则
,则
其公差是 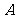

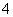

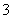


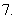 (
(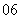 陕西文) 已知等差数列
陕西文) 已知等差数列 中,
中,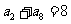 ,则该数列前
,则该数列前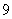 项和
项和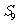 等于
等于
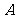
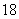

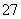

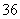

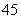
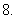 (
(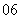 江西文) 在各项均不为零的等差数列
江西文) 在各项均不为零的等差数列 中,若
中,若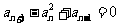
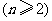 ,则
,则






 (
( 全国Ⅰ文) 设
全国Ⅰ文) 设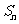 是等差数列
是等差数列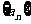 的前
的前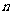 项和,若
项和,若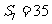 ,则
,则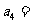


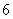

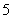
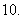 (
(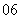 山东文) 等差数列
山东文) 等差数列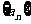 中,
中,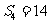 ,
, ,则
,则
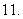 (
( 上海春)设
上海春)设 ,利用课本中推导等差数列前
,利用课本中推导等差数列前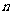 项和的公式的方法,可求得
项和的公式的方法,可求得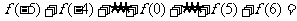
 (
( 湖南)已知数列
湖南)已知数列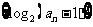 (
(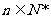 )为等差数列,且
)为等差数列,且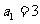 ,
,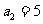 ,则
,则
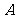




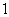

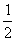
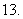 (
(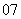 海南)已知
海南)已知 是等差数列,
是等差数列, ,其前
,其前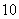 项和
项和 ,则其公差
,则其公差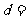
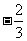



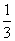

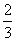
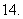 (
(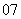 陕西文)等差数列
陕西文)等差数列 的前
的前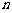 项和为
项和为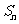 ,若
,若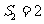 ,
, ,则
,则 等于
等于
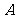


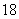



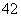
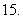 (
(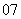 辽宁)设等差数列
辽宁)设等差数列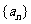 的前
的前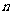 项和为
项和为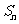 ,若
,若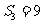 ,
,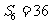 ,则
,则
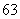

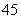

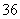

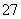
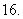 (
(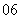 北京文)设等差数列
北京文)设等差数列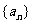 的首项
的首项 及公差
及公差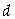 都是整数,前
都是整数,前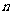 项和为
项和为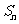 ,
,
(Ⅰ)若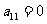 ,
, ,求数列的通项公式;
,求数列的通项公式;
(Ⅱ)若 ≥
≥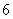 ,
, ,
,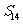 ≤
≤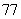 ,,求所有可能的数列
,,求所有可能的数列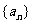 的通项公式.
的通项公式.
 (
(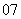 重庆)已知各项均为正数的数列
重庆)已知各项均为正数的数列 的前
的前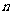 项和
项和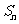 满足
满足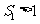 ,
,
且 ,(
,(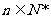 ).
).
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设数列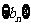 满足
满足 ,并记
,并记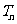 为
为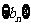 的前
的前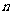 项和,
项和,
求证: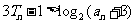 (
(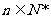 ).
).
 (
(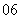 江苏)设数列
江苏)设数列 、
、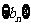 、
、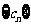 满足:
满足: ,
,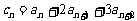 (
(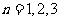 ,…)证明
,…)证明 为等差数列的充分必要条件是
为等差数列的充分必要条件是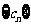 为等差数列且
为等差数列且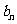 ≤
≤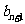 (
(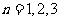 ,…)
,…)
 (
( 宿迁模拟)已知数列
宿迁模拟)已知数列 中
中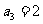 ,
, ,若
,若 为等差数列,则
为等差数列,则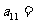






 (
(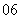 潍坊模拟)等差数列
潍坊模拟)等差数列 中,
中,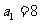 ,
,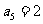 ,若在每相邻两项之间各插入一个数,使之成为等差数列,那么新的等差数列的公差是
,若在每相邻两项之间各插入一个数,使之成为等差数列,那么新的等差数列的公差是 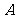
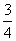

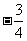



 在等差数列
在等差数列 中,
中,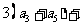
 ,则此数列的前
,则此数列的前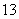 项之和等于
项之和等于
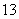




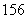
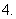 (
(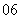 江南十校)已知函数
江南十校)已知函数 ,数列
,数列 满足
满足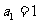 ,
,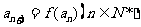
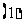 求证:数列
求证:数列 是等差数列;
是等差数列;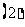 记
记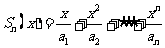 ,求
,求 .
.
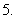 (
( 汕头模拟)已知数列
汕头模拟)已知数列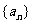 中,
中,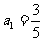 ,数列
,数列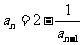
(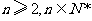 )数列
)数列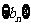 满足
满足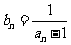 (
(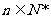 ).
).
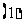 求证:数列
求证:数列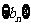 是等差数列;
是等差数列;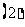 求数列
求数列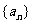 的最大项与最小项,并说明理由.
的最大项与最小项,并说明理由.
 填空:
填空: 若一个等差数列前
若一个等差数列前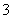 项的和为
项的和为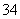 ,最后三项的和为
,最后三项的和为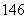 ,且所有项的和为
,且所有项的和为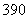 ,则这个数列有 项;
,则这个数列有 项;
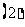 等差数列前
等差数列前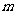 项和是
项和是 ,前
,前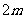 项和是
项和是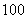 ,则它的前
,则它的前 项和是
项和是
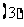 若
若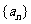 是公差为
是公差为 的等差数列,如果
的等差数列,如果 ,那么
,那么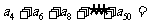
 含
含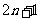 个项的等差数列其奇数项的和与偶数项的和之比为
个项的等差数列其奇数项的和与偶数项的和之比为
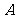
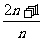

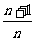

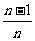

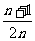
 已知
已知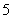 个数成等差数列,它们的和为
个数成等差数列,它们的和为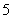 ,平方和为
,平方和为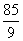 ,求这
,求这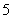 个数
个数
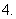 等差数列
等差数列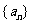 中共有
中共有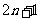 项,且此数列中的奇数项之和为
项,且此数列中的奇数项之和为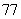 ,偶数项之和为
,偶数项之和为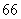 ,
,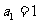 ,求其项数和中间项.
,求其项数和中间项.
问题1. (
( 全国)设数列
全国)设数列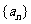 是递增等差数列,前三项的和为
是递增等差数列,前三项的和为 ,前三项的
,前三项的
积为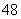 ,求
,求
 (
(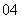 全国Ⅰ文)等差数列
全国Ⅰ文)等差数列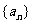 的前
的前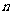 项和记为
项和记为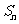 ,已知
,已知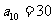 ,
,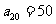 , ①求通项
, ①求通项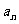 ; ② 若
; ② 若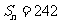 ,求
,求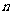
问题2. (
( 北京春)在等差数列
北京春)在等差数列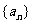 中,已知
中,已知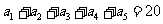 ,
,
则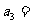

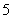

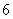

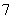
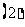 (
( 届高三湖南师大附中第二次月考)在等差数列
届高三湖南师大附中第二次月考)在等差数列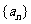 中,
中,
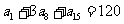 ,则
,则


 22
22  20
20 
 (
( 全国理Ⅱ)等差数列
全国理Ⅱ)等差数列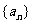 中,
中,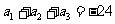 ,
, ,
,
则此数列前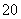 项和等于
项和等于 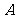




 (
(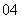 东北三校)设等差数列
东北三校)设等差数列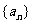 的前
的前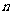 项和记为
项和记为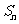 ,若
,若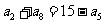 ,
,
则


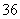

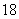
问题3.设等差数列 的前
的前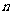 项和为
项和为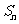 ,已知
,已知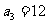 ,
,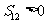 ,
,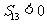 (Ⅰ)求公差
(Ⅰ)求公差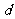 的取值范围;
(Ⅱ)指出
的取值范围;
(Ⅱ)指出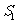 ,
,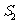 ,…,
,…, ,中哪一个值最大,并说明理由
,中哪一个值最大,并说明理由
问题4.等差数列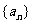 中,
中,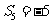 ,
,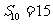 ,求数列
,求数列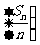 的前
的前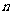 项和
项和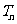
问题5. 已知数列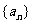 的前项和为
的前项和为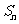 ,且
,且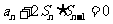
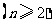 ,
,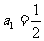
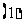 求证:
求证: 为等差数列,
为等差数列,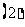 求
求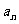 的表达式.
的表达式.
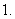 涉及等差数列的基本概念的问题,常用基本量
涉及等差数列的基本概念的问题,常用基本量 来处理;
来处理;
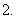 若奇数个成等差数列且和为定值时,可设中间三项为
若奇数个成等差数列且和为定值时,可设中间三项为 ;若偶数个成等差数列且和为定值时,可设中间两项为
;若偶数个成等差数列且和为定值时,可设中间两项为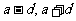 ,其余各项再根据等差数列的定义进行对称设元.
,其余各项再根据等差数列的定义进行对称设元.
 等差数列的相关性质:
等差数列的相关性质:
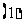 等差数列
等差数列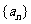 中,
中, ,变式
,变式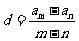 ;
;
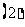 等差数列
等差数列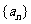 的任意连续
的任意连续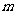 项的和构成的数列
项的和构成的数列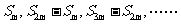 仍为等差数列.
仍为等差数列.
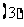 等差数列
等差数列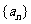 中,若
中,若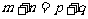 ,则
,则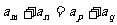 ,
,
若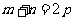 ,则
,则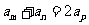
 等差数列
等差数列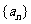 中,
中,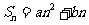 (其中
(其中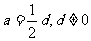 )
)
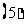 两个等差数列
两个等差数列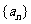 与
与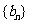 的和差的数列
的和差的数列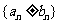 仍为等差数列.
仍为等差数列.
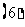 若
若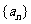 是公差为
是公差为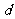 的等差数列,则其子列
的等差数列,则其子列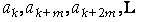 也是等差数列,
也是等差数列,
且公差为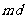 ;
; 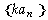 也是等差数列,且公差为
也是等差数列,且公差为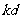
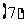 在项数为
在项数为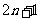 项的等差数列
项的等差数列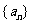 中,
中,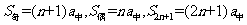 ;
;
在项数为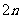 项的等差数列
项的等差数列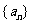 中
中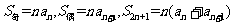 .
.
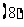 等差数列
等差数列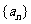 中,
中, 也是一个等差数列,即点
也是一个等差数列,即点 (
(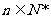 )在一条直线上; 点
)在一条直线上; 点 (
(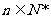 )在一条直线上.
)在一条直线上.
 两个等差数列
两个等差数列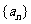 与
与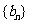 中,
中,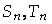 分别是它们的前
分别是它们的前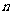 项和,则
项和,则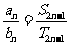 .
.
|
|
等差数列 |
等比数列 |
|
定义 |
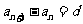 ( (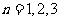 ,…) ,…) |
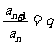 ( (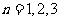 ,…) ,…) |
|
通项公式 |
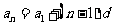 , ,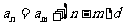 |
 , , |
|
求和 公式 |
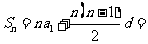 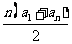 |
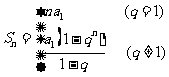 |
|
中项 公式 |
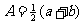 |
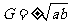 |
|
对称性 |
若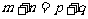 ,则 ,则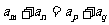 |
若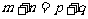 ,则 ,则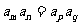 |
|
分段和原理 |
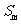 、 、 、 、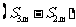 成等差数列 成等差数列 |
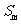 、 、 、 、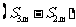 成等比数列 成等比数列 |
 等差数列的判定方法:
等差数列的判定方法:
 定义法:
定义法: 常数(
常数(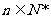 )
)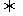
 为等差数列;
为等差数列;
 中项公式法:
中项公式法: (
(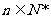 )
)
 为等差数列;
为等差数列;
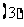 通项公式法:
通项公式法: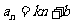 (
(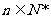 )
)
 为等差数列;
为等差数列;
 前
前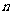 项求和法:
项求和法: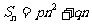 (
(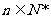 )
)
 为等差数列;
为等差数列;
 (
(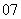 广东)已知数列
广东)已知数列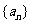 的前
的前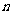 项和
项和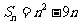 ,第
,第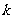 项满足
项满足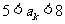 ,则
,则
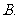
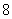
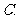
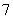
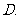

 (
(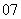 北京文)若数列
北京文)若数列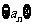 的前
的前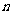 项和
项和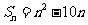
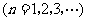 ,则此数列的通项公式为
,则此数列的通项公式为
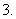 (
( 江西)已知数列
江西)已知数列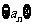 对于任意
对于任意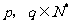 ,有
,有 ,若
,若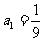 ,则
,则
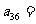
 (
( 全国)已知数列
全国)已知数列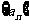 的前
的前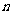 项和
项和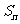 满足
满足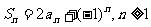
 写出数列
写出数列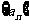 的前三项
的前三项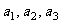 ;
;
 求数列
求数列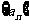 的通项公式;
的通项公式;
 (
( 全国Ⅰ)已知数列
全国Ⅰ)已知数列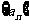 中
中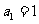 ,且
,且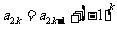 ,
,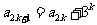
其中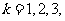 … (Ⅰ)求
… (Ⅰ)求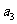 ,
, (Ⅱ)求
(Ⅱ)求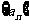 的通项公式.
的通项公式.
 (
( 全国)已知数列
全国)已知数列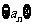 ,满足
,满足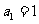 ,
,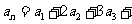 …
…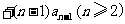 ,则
,则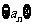 的通项
的通项
 (
( 天津)在数列
天津)在数列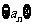 中,
中,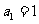 ,
,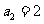 ,且
,且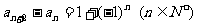 ,
,
则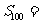
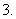 已知数列
已知数列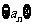 中,
中,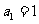 ,对所有的
,对所有的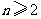 ,都有
,都有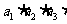 …
…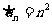 ,则
,则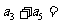

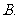
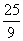
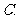
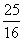
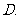
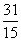
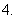 数列
数列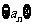 中,
中,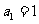 ,
,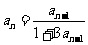 (
(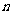 ≥
≥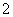 ),则
),则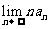 等于
等于
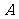
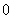
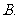

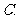
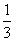
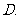 不存在
不存在
 数列
数列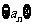 中,
中,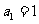 ,
,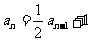 (
(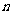 ≥
≥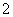 )求其通项公式.
)求其通项公式.
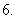 数列
数列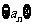 满足
满足
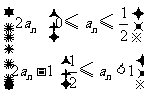 ,若
,若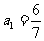 ,则
,则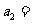 ;
;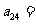
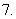 (
( 重庆)在数列
重庆)在数列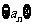 中,若
中,若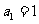 ,
,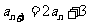 (
(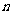 ≥
≥ ),则该数列的通项
),则该数列的通项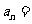
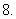 已知
已知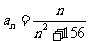
 ,则数列
,则数列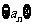 的最大项是
的最大项是
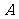
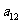
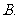
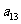
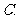
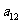 或
或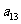
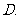 不存在
不存在
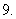 (
(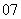 南通市九校联考)已知数列
南通市九校联考)已知数列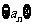 中,
中,
 ,则在数列
,则在数列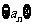 的前
的前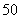 项中最小项和最大项分别是
项中最小项和最大项分别是
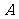
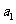 ,
,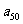
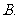
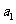 ,
,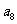
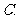
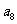 ,
,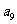
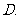
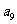 ,
,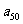
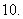 已知函数
已知函数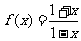 ,设数列
,设数列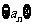 满足:
满足: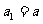 (
(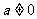 且
且 ),
),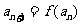 ,
,
 为数列
为数列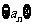 的前
的前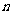 项和.
项和. 若
若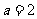 ,求
,求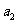 ,
,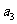 ,
,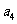 ;
;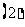 求证:数列
求证:数列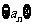 是周期数列;
是周期数列; 探究:是否存在满足
探究:是否存在满足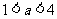 的
的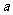 ,使
,使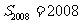 ?
?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com