
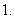 解含绝对值的不等式的基本思想是去掉绝对值符号,将其等价转化为一元一次(二次)
解含绝对值的不等式的基本思想是去掉绝对值符号,将其等价转化为一元一次(二次)
不等式(组)进行求解;
去掉绝对值的主要方法有:
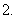 (1)公式法:
(1)公式法: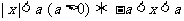 ,
, 或
或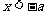 .
.
(2)定义法: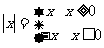 ,零点分段法;
,零点分段法;
(3)平方法:不等式两边都是非负时,两边同时平方.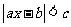

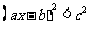
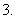 解绝对值不等式的其他方法:
解绝对值不等式的其他方法:
(1)利用绝对值的几何意义法:
(2) 利用函数图象法:原理:不等式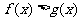 的解集是函数
的解集是函数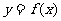 的图象位于
的图象位于
函数 的图象上方的点的横坐标的集合.
的图象上方的点的横坐标的集合.
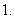 绝对值的几何意义:
绝对值的几何意义: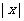 是指数轴上点
是指数轴上点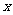 到原点的距离;
到原点的距离;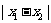 是指数轴上
是指数轴上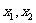 两
两
点间的距离.
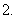 当
当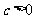 时,
时,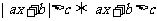 或
或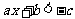 ;
;
 ;
;
当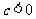 时,
时,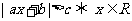 ,
,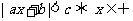 .
.
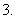 设
设 ,则不等式
,则不等式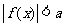 等价于
等价于 或
或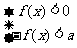 ,也可以等价于
,也可以等价于
 ;
;
设 ,则不等式
,则不等式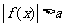 等价于
等价于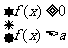 或
或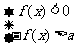 ,也可以等价于
,也可以等价于
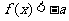 或
或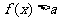 ;
;
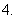 设
设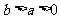 ,则不等式
,则不等式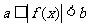
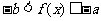 或
或

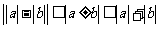

 ≥
≥
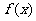 ≥
≥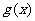 或
或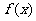 ≤
≤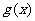 ;
;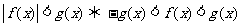
 (
( 北京)已知
北京)已知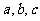 满足
满足 ,且
,且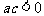 ,那么下列选项中不一定成立的是
,那么下列选项中不一定成立的是
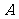

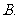
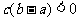
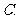
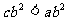
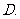

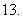 (
(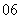 上海春)14. 若
上海春)14. 若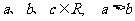 ,则下列不等式成立的是
,则下列不等式成立的是
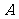
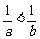
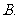
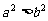
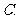

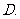
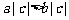
 (
(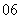 江西)若
江西)若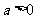 ,
,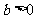 ,则不等式
,则不等式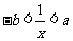 等价于
等价于
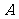
 或
或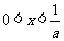
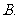
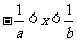
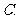
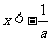 或
或
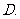
 或
或
 (
( 届高三北京海淀第二学期期末)若
届高三北京海淀第二学期期末)若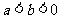 ,则下列结论不正确的是
,则下列结论不正确的是
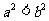
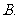
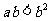
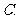

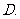

 设
设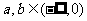 ,则“
,则“ ”是“
”是“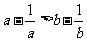 ”成立的
”成立的
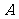 充分非必要条件
充分非必要条件 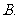 必要非充分条件
必要非充分条件 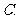 充要条件
充要条件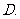 既不充分也不必要条件
既不充分也不必要条件
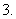 下列不等式:
下列不等式: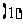
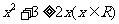 ,
, 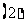
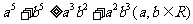 ,
,
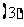
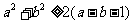 .其中正确的个数为
.其中正确的个数为 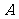

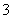
 在下列命题中真命题的个数有 ①若
在下列命题中真命题的个数有 ①若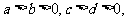 那么
那么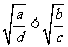 ;
;
②已知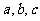 都是正数,并且
都是正数,并且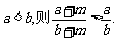 ③
③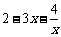 的最大值是
的最大值是
④若 ,则
,则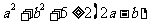
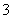 个
个 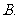
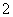 个
个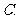
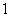 个
个 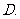
 个
个
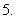 给出下列条件①
给出下列条件①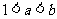 ;②
;②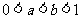 ;③
;③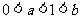 .其中,能推出
.其中,能推出
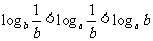 成立的条件的序号是
(填所有可能的条件的序号)
成立的条件的序号是
(填所有可能的条件的序号)
 已知
已知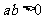 ,试比较
,试比较 与
与 的大小.
的大小.
 已知
已知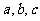 满足:
满足: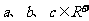 ,
,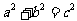 ,当
,当 ,
,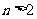 时,比较
时,比较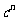 与
与 的大小.
的大小.
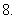 设
设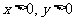 且
且 ,比较
,比较 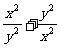 与
与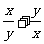 的大小
的大小
 已知
已知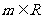 ,
,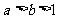 ,
,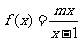 ,试比较
,试比较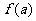 与
与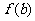 的大小.
的大小.
 设
设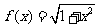 ,比较
,比较 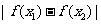 与
与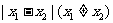 的大小.
的大小.
 设
设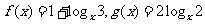 ,其中
,其中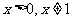 ,比较
,比较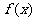 与
与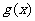 的大小.
的大小.
问题1.若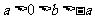 ,
,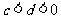 ,则下列命题:
,则下列命题: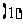
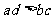 ;
;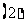
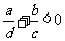 ;
;
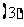
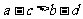 ;
;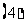
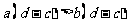 中能成立的个数是
中能成立的个数是 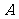
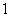
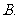
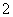
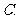
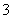
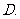
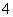
问题2.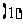 若
若 ,试比较
,试比较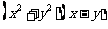 与
与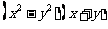 的大小;
的大小;
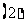 设
设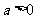 ,
,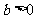 ,且
,且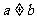 ,试比较
,试比较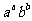 与
与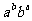 的大小.
的大小.
 设
设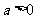 ,
,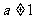 ,
, ,比较
,比较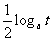 与
与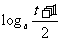 的大小,
的大小,
问题3.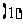 已知
已知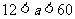 ,
,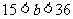 ,求
,求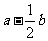 及
及 的取值范围;
的取值范围;
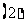 若
若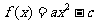 满足
满足 ≤
≤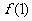 ≤
≤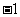 ,
,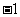 ≤
≤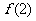 ≤
≤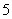 ,求
,求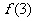 的取值范围.
的取值范围.
问题4.已知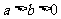 ,
, ,用不等式性质证明:
,用不等式性质证明:
比较两数大小的一般方法是:作差比较法与作商比较法.
不等式的性质:①对称性: ;②传递性:
;②传递性: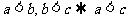 .
.
③可加性: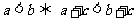 ;④加法性质:
;④加法性质: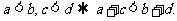
⑤移项法则: ⑥可乘性:
⑥可乘性: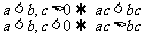 ;
;
⑦乘法性质: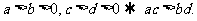 ⑧乘方性质:
⑧乘方性质: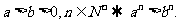 ⑨开方性质:
⑨开方性质: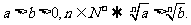
⑩倒数法则: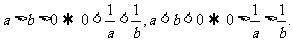
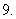 (
( 湖北)将
湖北)将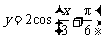 的图象按向量
的图象按向量 平移,则平移后所得图象的解析式为
平移,则平移后所得图象的解析式为 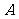
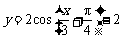
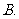
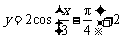
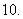 (
( 全国Ⅱ)已知点
全国Ⅱ)已知点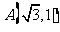 ,
, ,
, ,设
,设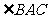 的平分线
的平分线 与
与 相交于
相交于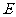 ,那么有
,那么有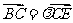 ,其中
,其中 等于
等于 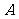
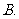

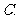

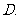
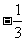
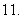 (
( 湖北)设函数
湖北)设函数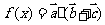 ,其中向量
,其中向量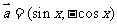 ,
,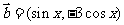 ,
,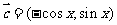 ,
,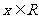 .(Ⅰ)求函数
.(Ⅰ)求函数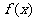 的最大值和最小正周期;(Ⅱ)将函数
的最大值和最小正周期;(Ⅱ)将函数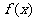 的图像按向量
的图像按向量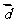 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的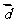 .
.
 若直线
若直线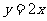 按向量
按向量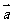 平移得到直线
平移得到直线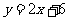 ,那么
,那么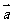 ( )
( )
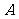 只能是
只能是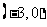
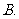 只能是
只能是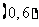
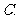 只能是
只能是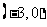 或
或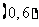
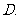 有无数个
有无数个
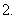 若点
若点 分
分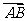 的比为
的比为 ,则点
,则点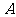 分
分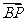 的比是
的比是
 已知向量
已知向量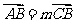
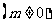 ,则
,则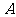 分
分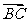 的定分比的值为
的定分比的值为
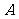
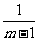
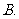
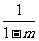
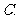

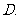

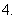 把函数
把函数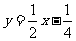 的图象,按向量
的图象,按向量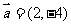 平移后,图象的解析式是
平移后,图象的解析式是
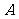
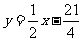
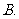
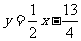
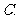
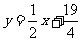

 函数
函数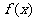
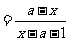 的反函数
的反函数 的图象的对称中心是
的图象的对称中心是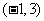 ,则实数
,则实数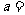
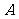
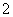
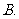
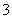
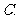

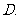

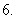 曲线
曲线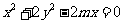 按
按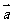
 平移后,得到曲线
平移后,得到曲线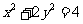 ,则
,则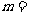
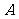
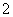
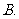

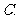

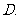

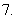 将函数
将函数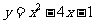 顶点
顶点 按向量
按向量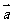 平移后得到点
平移后得到点 ,则
,则
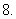
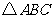 中三边中点分别是
中三边中点分别是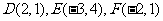 ,则
,则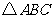 的重心是
的重心是
问题1.已知两点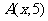 ,
, ,点
,点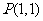 在直线
在直线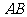 上,且
上,且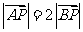 ,
,
求点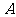 和点
和点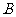 的坐标.
的坐标.
问题2.已知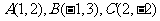 ,点
,点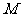 分
分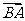 的比
的比 为
为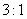 ,点
,点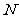 在线段
在线段 上,且
上,且 ,求点
,求点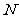 的坐标.
的坐标.
问题3.已知函数
 的图象经过按
的图象经过按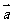 平移后使得抛物线顶点在
平移后使得抛物线顶点在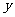 轴上,且在
轴上,且在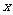 轴上截得的弦长为
轴上截得的弦长为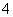 ,求平移后函数解析式和
,求平移后函数解析式和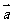 .
.
问题4.定点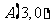 为圆
为圆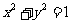 外一点,
外一点, 为圆上的动点,
为圆上的动点,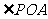 的平分线交
的平分线交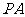 于
于 , 求
, 求 点的轨迹方程
点的轨迹方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com