
 问题1. (
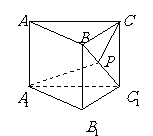
问题1. ( 江西)如图,在直三棱柱
江西)如图,在直三棱柱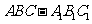 中,底面为直角三角形,
中,底面为直角三角形, ,
,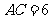 ,
,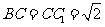 ,
,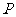 是
是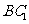 上一动点,则
上一动点,则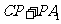 的最小值
的最小值
是
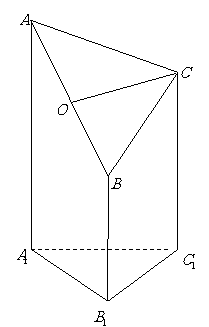
 问题2.将如图
问题2.将如图 所示的直角梯形
所示的直角梯形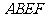 (图中所示数字为对应线段长度)沿直线
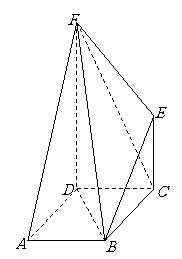
(图中所示数字为对应线段长度)沿直线 折成直二面角,连结部分线段后围成一个空间几何体,如图
折成直二面角,连结部分线段后围成一个空间几何体,如图 所示,
所示,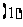 求异面直线
求异面直线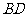 与
与 所成角的大小;
所成角的大小;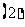 求二面角
求二面角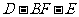 的大小;
的大小;
 这五个点在同一球面上,求该球的表面积.
这五个点在同一球面上,求该球的表面积.

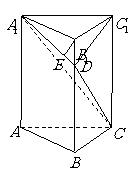
问题3.( 江西)右图是一个直三棱柱(以
江西)右图是一个直三棱柱(以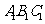 为底面)被一平面所截得到的
为底面)被一平面所截得到的
 几何体,截面为
几何体,截面为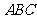 .已知
.已知 ,
,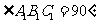 ,
, ,
,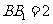 ,
,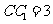 .
.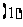 设点
设点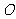 是
是 的中点,证明:
的中点,证明: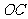 ∥平面
∥平面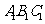
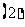 求二面角
求二面角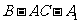 的大小;
的大小;
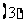 求此几何体的体积 .
求此几何体的体积 .
 问题4. (
问题4. ( 重庆)如图,在直三棱柱
重庆)如图,在直三棱柱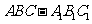 中,
中,
 ,
,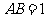 ,
,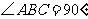 ;点
;点 分别在
分别在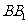 ,
,
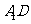 上,且
上,且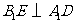 ,四棱锥
,四棱锥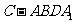 与直三棱柱的
与直三棱柱的
体积之比为 .
.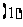 求异面直线
求异面直线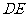 与
与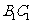 的距离;
的距离;
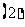 若
若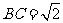 ,求二面角
,求二面角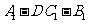 的平面角的正切值.
的平面角的正切值.

折叠问题的计算与证明: 一定要关注“变量”和“不变量”在证明和计算中的应用:折叠时位于棱同侧的位置关系和数量关系不变;位于棱两侧的位置关系与数量关系变,
一定要关注“变量”和“不变量”在证明和计算中的应用:折叠时位于棱同侧的位置关系和数量关系不变;位于棱两侧的位置关系与数量关系变, 折前折后的图形结合起来使用.
折前折后的图形结合起来使用.
 (
( 陕西)一个正三棱锥的四个顶点都在半径为
陕西)一个正三棱锥的四个顶点都在半径为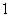 的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是
的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 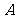

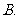
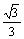
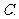
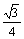
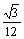
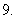 (
( 辽宁)若一个底面边长为
辽宁)若一个底面边长为 ,棱长为
,棱长为 的正六棱柱的所有顶点都在一个平面上,则此球的体积为
的正六棱柱的所有顶点都在一个平面上,则此球的体积为
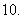 (
( 全国Ⅱ)一个正四棱柱的各个顶点在一个直径为
全国Ⅱ)一个正四棱柱的各个顶点在一个直径为 的球面上。如果正四棱柱的底面边长为
的球面上。如果正四棱柱的底面边长为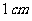 ,那么该棱柱的表面积为
,那么该棱柱的表面积为
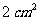
 正方体、正多面体、凸多面体、简单多面体是什么关系?
正方体、正多面体、凸多面体、简单多面体是什么关系?
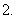 已知凸多面体每个面都是五边形,每个顶点都有三条棱相交,试求该凸多面体的面数、顶点数和棱数.
已知凸多面体每个面都是五边形,每个顶点都有三条棱相交,试求该凸多面体的面数、顶点数和棱数.
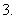 一个广告气球被一束入射角为
一个广告气球被一束入射角为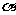 的平行光线照射,其投影是一个长半轴为
的平行光线照射,其投影是一个长半轴为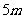 的椭圆,则制作这个广告气球至少需要的面料是
的椭圆,则制作这个广告气球至少需要的面料是
 在球面上有四个点
在球面上有四个点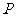 、
、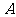 、
、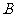 、
、 ,如果
,如果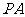 、
、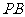 、
、 两两互相垂直,且
两两互相垂直,且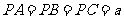 ,那么这个球面的面积是
,那么这个球面的面积是 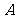

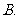
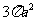
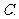
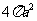
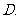
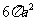
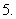 北纬
北纬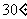 的圆把北半球面积分为两部分,这两部分面积的比为
的圆把北半球面积分为两部分,这两部分面积的比为
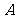
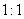
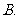
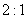
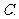
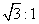
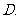
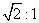
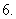 已知过球面上
已知过球面上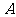 、
、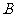 、
、 三点的截面和球心的距离等于球半径的一半,
三点的截面和球心的距离等于球半径的一半,
且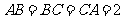 ,则球面面积是
,则球面面积是
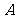

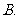
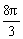
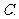
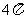
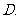
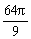
 正八面体的相邻两个面所成二面角的大小为
正八面体的相邻两个面所成二面角的大小为
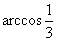
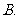



问题1. (
(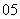 辽宁)棱长为
辽宁)棱长为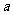 的正方体,连结相邻面的中心,以这些线段为棱的
的正方体,连结相邻面的中心,以这些线段为棱的
八面体的体积为 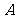
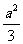
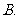

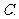

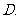
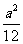
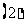 已知一个正四面体和一个正八面体的棱长相等且为
已知一个正四面体和一个正八面体的棱长相等且为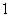 ,把它们拼起来,使一个表面重合,所得的多面体有多少个面?
,把它们拼起来,使一个表面重合,所得的多面体有多少个面?
问题2. (
( 天津)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为
天津)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 ,则此球的表面积为
,则此球的表面积为
 (
( 全国Ⅰ文)正四棱锥
全国Ⅰ文)正四棱锥 的底面边长和各侧棱长都为
的底面边长和各侧棱长都为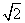 ,点
,点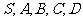
都在同一个球面上,则该球的体积为
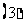 (
( 江西文)四面体
江西文)四面体 的外接球球心在
的外接球球心在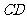 上,且
上,且 ,
,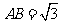 ,
,
在外接球面上两点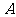 、
、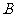 间的球面距离是
间的球面距离是 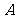
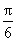
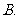
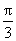
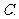
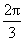

 (
(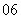 陕西)水平桌面
陕西)水平桌面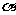 上放有
上放有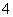 个半径均为
个半径均为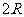 的球,且相邻的球都相切(球心的连线构成正方形).在这
的球,且相邻的球都相切(球心的连线构成正方形).在这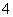 个球的上面放
个球的上面放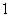 个半径为
个半径为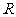 的小球,它和下面
的小球,它和下面 个球恰好都相切,则小球的球心到水平桌面
个球恰好都相切,则小球的球心到水平桌面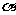 的距离是
的距离是
 问题3. (
问题3. ( 四川)设球
四川)设球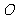 的半径是
的半径是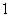 ,
,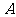 、
、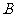 、
、 是球面上三点,已知
是球面上三点,已知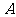 到
到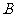 、
、 两点的球面距离都是
两点的球面距离都是 ,且二面角
,且二面角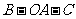 的大小为
的大小为 ,则从
,则从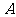 点沿球面经
点沿球面经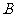 、
、 两点再回到
两点再回到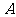 点的最短距离是
点的最短距离是
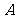
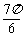
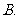
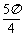
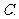
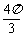
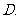
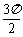
问题4.三棱锥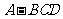 的两条棱
的两条棱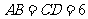 ,其余各棱长均为
,其余各棱长均为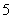 ,求三棱锥的内切球半径和外接球半径.
,求三棱锥的内切球半径和外接球半径.
问题5.已知球的半径为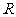 ,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
 每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
 正多面体有且只有
正多面体有且只有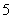 种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
 简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.
简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.
说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
 五种正多面体的顶点数、面数及棱数:
五种正多面体的顶点数、面数及棱数:
|
正多面体 |
顶点数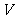 |
面数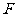 |
棱数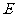 |
|
正四面体 |
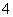 |
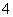 |
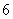 |
|
正六面体 |
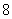 |
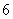 |
 |
|
正八面体 |
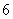 |
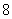 |
 |
|
正十二面体 |
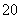 |
 |
 |
|
正二十面体 |
 |
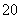 |
 |
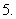 欧拉定理(欧拉公式):简单多面体的顶点数
欧拉定理(欧拉公式):简单多面体的顶点数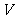 、面数
、面数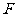 及棱数
及棱数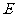 有关系式:
有关系式:
 计算棱数
计算棱数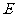 常见方法:
常见方法: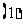
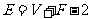 ;
;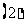
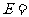 各面多边形边数和的一半;
各面多边形边数和的一半;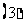
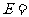 顶点数与共顶点棱数积的一半.
顶点数与共顶点棱数积的一半.
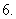 球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球
球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径
定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球
与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球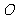
 球的截面:用一平面
球的截面:用一平面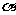 去截一个球
去截一个球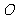 ,设
,设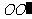 是平面
是平面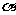 的垂线段,
的垂线段, 为垂足,且
为垂足,且 ,所得的截面是以球心在截面内的射影为圆心,以
,所得的截面是以球心在截面内的射影为圆心,以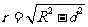 为半径的一个圆,截面是一个圆面.
为半径的一个圆,截面是一个圆面.
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆
 两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离.
两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离.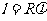 (
(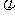 为球心角的弧度数).
为球心角的弧度数).
 球的表面积和体积公式:
球的表面积和体积公式: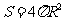 ,
, .
.
 (
( 安徽)在正方体上任意选择
安徽)在正方体上任意选择 个顶点,它们可能是如下各种几何形体的
个顶点,它们可能是如下各种几何形体的 个顶点,这些几何形体是 (写出所有正确结论的编号).
个顶点,这些几何形体是 (写出所有正确结论的编号).
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.  (
( 北京春) 两个完全相同的长方体的长、宽、高分别为
北京春) 两个完全相同的长方体的长、宽、高分别为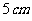 ,
,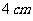 ,
,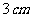 ,
,
把它们重叠在一起组成一个新长方体,在这些新长方体中,最长的对角线的长度是
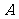

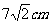
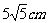

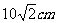
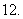 (
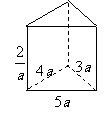
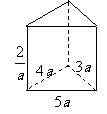
(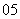 上海)有两个相同的直三棱柱,高为
上海)有两个相同的直三棱柱,高为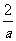 ,底面
,底面
三角形的三边长分别为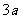 、
、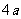 、
、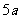 (
( ).用它们
).用它们
拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积
最小的是一个四棱柱,则 的取值范围是
的取值范围是
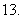 (
(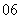 上海春)正四棱锥底面边长为
上海春)正四棱锥底面边长为 ,侧棱长为
,侧棱长为 ,则其体积为
,则其体积为
 (
( 全国Ⅰ)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为
全国Ⅰ)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为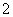 ,则该三角形的斜边长为
,则该三角形的斜边长为
 (
( 江苏)正三棱锥
江苏)正三棱锥 高为
高为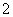 ,侧棱与底面所成角为
,侧棱与底面所成角为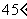 ,则点
,则点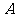 到侧面
到侧面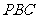 的距离是
的距离是
 一个正三棱锥与一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,这个组合体可能是
一个正三棱锥与一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,这个组合体可能是
 正四棱锥
正四棱锥
 正五棱锥
正五棱锥
 斜三棱柱
斜三棱柱  正三棱柱
正三棱柱
 如果三棱锥
如果三棱锥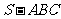 的底面是不等边三角形,侧面与底面所成的二面角相等,且
的底面是不等边三角形,侧面与底面所成的二面角相等,且
顶点 在底面的射影为
在底面的射影为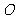 ,
,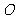 在
在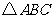 内,那么
内,那么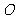 是
是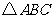 的
的
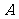 垂心
垂心 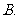 重心
重心 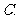 外心
外心  内心
内心
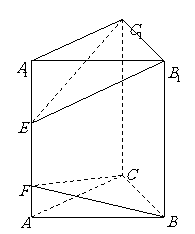
 如图,在直三棱柱
如图,在直三棱柱 中,
中, ,
,
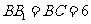 ,
, 、
、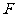 为侧棱
为侧棱 上的两点,且
上的两点,且 ,
,
则多面体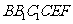 的体积等于
的体积等于
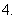 过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为
过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为
 在三棱锥
在三棱锥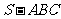 中,
中, ,则侧棱
,则侧棱 与侧面
与侧面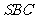 所成的角的大小是
所成的角的大小是
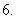 三棱锥一条侧棱长是
三棱锥一条侧棱长是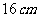 ,和这条棱相对的棱长是
,和这条棱相对的棱长是 ,其余四条棱长都是
,其余四条棱长都是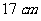 ,求棱锥的体积.
,求棱锥的体积.
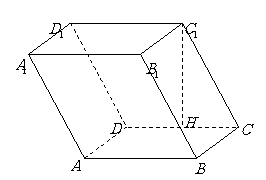
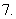 平行六面体
平行六面体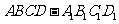 的底面是矩形,
的底面是矩形,
侧棱长为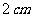 ,点
,点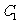 在底面
在底面 上的射影
上的射影
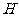 是
是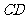 的中点,
的中点,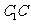 与底面
与底面 成
成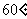 角,
角,
二面角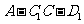 为
为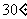 ,求该平行六面体
,求该平行六面体
的表面积和体积.
 (
( 届高三合肥市三检)正三棱柱
届高三合肥市三检)正三棱柱 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为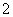 ,过正三棱柱
,过正三棱柱 底面上的一条棱
底面上的一条棱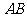 作一平面与底面成
作一平面与底面成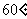 的平面角,则该平面与平面
的平面角,则该平面与平面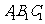 所截得的线段长等于
所截得的线段长等于
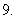 (
( 届高三宝鸡中学第四次月考)在直四棱柱
届高三宝鸡中学第四次月考)在直四棱柱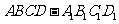 中,
中, ,
, 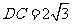 ,
, ,
,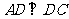 ,
,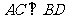 垂足为
垂足为 .
.
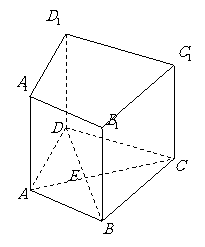
 求证:
求证: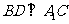 ;
;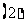 求异面直线
求异面直线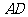 与
与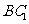 所成的角.
所成的角.
问题1. (
( 全国Ⅱ文)下面是关于三棱锥的四个命题:
全国Ⅱ文)下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中,真命题的编号是 (写出所有真命题的编号)
 (
( 江西文)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下
江西文)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下 个命题中,假命题是
个命题中,假命题是
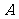 等腰四棱锥的腰与底面所成的角都相等
等腰四棱锥的腰与底面所成的角都相等
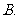 等腰四棱锥的侧面与底面所成的二面角都相等或互补
等腰四棱锥的侧面与底面所成的二面角都相等或互补
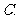 等腰四棱锥的底面四边形必存在外接圆
等腰四棱锥的底面四边形必存在外接圆
 等腰四棱锥的各顶点必在同一球面上
等腰四棱锥的各顶点必在同一球面上
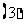 (
( 全国)下面是关于四棱柱的四个命题:
全国)下面是关于四棱柱的四个命题:
① 若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
② 若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;
③ 若四个侧面两两全等,则该四棱柱为直四棱柱;
④ 若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.
其中,真命题的编号是 (写出所有真命题的编号).
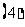 (
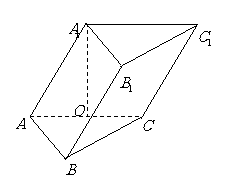
( 江西文)如右图,已知正三棱柱
江西文)如右图,已知正三棱柱
的底面边长为 ,高为
,高为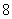 ,一质点自
,一质点自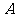 点出发,沿着三棱柱
点出发,沿着三棱柱
的侧面绕行两周到达 点的最短路线的长为
点的最短路线的长为
 问题2.三棱柱
问题2.三棱柱 中,
中,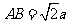 ,
,
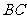 、
、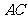 、
、 的长均为
的长均为 ,点
,点 在底面
在底面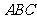
上的射影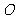 在
在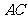 上.
上.
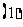 求
求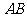 与侧面
与侧面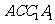 所成的角;
所成的角;
 若
若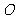 点恰是
点恰是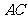 的中点,求此三棱柱的侧面积;
的中点,求此三棱柱的侧面积;
 求此三棱柱的体积.
求此三棱柱的体积.
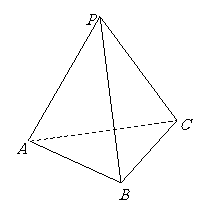 问题3.已知正四面体
问题3.已知正四面体 的棱长为
的棱长为 ,用一个
,用一个
平行于底面的平面截此四面体,所得的截面面积为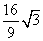 ,
,
求截面与底面之间的距离.
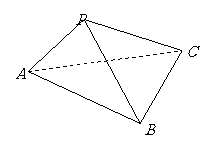
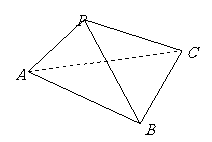
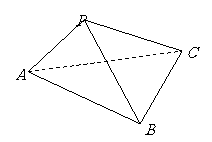 问题4.如图所示,三棱锥
问题4.如图所示,三棱锥 中,
中,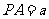 ,
,
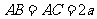 ,
,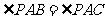
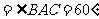 ,
,
求三棱锥 的体积.(要求用四种不同的方法)
的体积.(要求用四种不同的方法)

 有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.侧棱与底面垂直的棱柱叫做直棱柱.底面是正多边形的直棱柱叫正棱柱.
有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.侧棱与底面垂直的棱柱叫做直棱柱.底面是正多边形的直棱柱叫正棱柱.
 棱柱的各侧棱相等,各侧面都是平行四边形;长方体的对角线的平方等于由一个顶点出发的三条棱的平方和.
棱柱的各侧棱相等,各侧面都是平行四边形;长方体的对角线的平方等于由一个顶点出发的三条棱的平方和.
 一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.
一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.
 棱锥中与底面平行的截面与底面平行,并且它们面积的比等于对应高的平方比.
棱锥中与底面平行的截面与底面平行,并且它们面积的比等于对应高的平方比.
在正棱锥中,侧棱、高及侧棱在底面上的射影构成直角三角形;斜高、高及斜高在底面上的射影构成直角三角形.
 三棱锥的顶点在底面三角形上射影位置常见的有:
三棱锥的顶点在底面三角形上射影位置常见的有:
①
侧棱长相等 外心;②侧棱与底面所成的角相等
外心;②侧棱与底面所成的角相等 外心;
外心;
②
侧面与底面所成的角相等 内心;④顶点到底面三边的距离相等
内心;④顶点到底面三边的距离相等 内心;
内心;
⑤三侧棱两两垂直 垂心;⑥相对棱两两垂直
垂心;⑥相对棱两两垂直 垂心.
垂心.
 求体积常见方法有:①直接法(公式法);②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;⑥利用四面体的体积性质:(ⅰ)底面积相同的两个三棱锥体积之比等于其底面积的比;(ⅱ)高相同的两个三棱锥体积之比等于其底面积的比;(ⅲ)用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方.
求体积常见方法有:①直接法(公式法);②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;⑥利用四面体的体积性质:(ⅰ)底面积相同的两个三棱锥体积之比等于其底面积的比;(ⅱ)高相同的两个三棱锥体积之比等于其底面积的比;(ⅲ)用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com