
问题1.(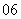 陕西文)甲、乙、丙
陕西文)甲、乙、丙 人投篮,投进的概率分别是
人投篮,投进的概率分别是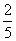 ,
,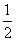 ,
,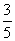 .现
.现 人各投篮
人各投篮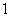 次,求:
次,求:
 人都投进的概率;
人都投进的概率;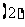
 人中恰有
人中恰有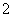 人投进的概率.
人投进的概率.
问题2.(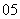 北京文)甲、乙两人各进行
北京文)甲、乙两人各进行 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为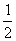 ,乙每次击中目标的概率
,乙每次击中目标的概率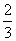 ,
,  甲恰好击中目标的
甲恰好击中目标的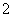 次的概率;
次的概率; 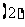 乙至少击中目标
乙至少击中目标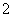 次的概率;
次的概率;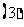 求乙恰好比甲多击中目标
求乙恰好比甲多击中目标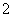 次的概率.
次的概率.
问题3.(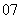 重庆文)设甲、乙两人每次射击命中目标的概率分别为
重庆文)设甲、乙两人每次射击命中目标的概率分别为 和
和 ,且各次射击相互独立.
,且各次射击相互独立. 若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
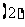 若甲、乙各射击两次,求两人命中目标的次数相等的概率.
若甲、乙各射击两次,求两人命中目标的次数相等的概率.
 相互独立事件:事件
相互独立事件:事件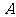 (或
(或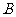 )是否发生对事件
)是否发生对事件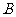 (或
(或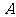 )发生的概率没有影响,这样的两个事件叫做相互独立事件.
)发生的概率没有影响,这样的两个事件叫做相互独立事件.
若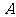 与
与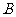 是相互独立事件,则
是相互独立事件,则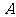 与
与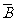 ,
, 与
与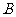 ,
, 与
与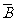 也相互独立.
也相互独立.
 互斥事件与相互独立事件是有区别的:
互斥事件与相互独立事件是有区别的:
两事件互斥是指同一次试验中两事件不能同时发生,两事件相互独立是指不同试验下,二者互不影响;两个相互独立事件不一定互斥,即可能同时发生,而互斥事件不可能同时发生.
 相互独立事件同时发生的概率:
相互独立事件同时发生的概率:
事件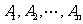 相互独立,
相互独立,  .
.
 独立重复试验的定义:在同样条件下进行的各次之间相互独立的一种试验.
独立重复试验的定义:在同样条件下进行的各次之间相互独立的一种试验.
 关于相互独立事件也要抓住以下特征加以理解:
关于相互独立事件也要抓住以下特征加以理解:
第一,相互独立也是研究两个事件的关系;第二,所研究的两个事件是在两次试验中得到的;第三,两个事件相互独立是从“一个事件的发生对另一个事件的发生的概率没有影响”来确定的.
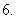 独立重复试验的概率公式:如果在一次试验中某事件发生的概率是
独立重复试验的概率公式:如果在一次试验中某事件发生的概率是 ,那么在
,那么在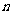 次独立重复试验中这个事恰好发生
次独立重复试验中这个事恰好发生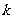 次的概率
次的概率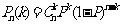
 表示事件
表示事件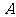 在
在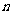 次独立重复试验中恰好发生了
次独立重复试验中恰好发生了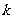 次的概率
次的概率
 关于独立重复试验要从三个方面理解:
关于独立重复试验要从三个方面理解:
第一:每次实验都在同样条件下进行;第二:各次实验中的事件是相互独立的;第三:每次实验只有两种结果,即事件要么发生,要么不发生,它与实验的序号无关.
 (
( 重庆文)若
重庆文)若 把钥匙中只有
把钥匙中只有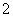 把能打开某锁,则从中任取
把能打开某锁,则从中任取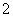 把能将该锁打开的概率为
把能将该锁打开的概率为
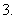 (
( 四川) 从
四川) 从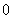 到
到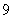 这
这 个数字中任取
个数字中任取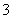 个数字组成一个没有重复数字的三位数,
个数字组成一个没有重复数字的三位数,
这个数不能被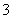 整除的概率为
整除的概率为 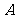
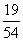

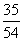
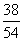

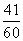
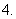 (
(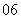 浙江)甲、乙两袋装有大小相同的红球和白球,甲袋装有
浙江)甲、乙两袋装有大小相同的红球和白球,甲袋装有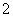 个红球,
个红球,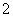 个白球;乙袋装有
个白球;乙袋装有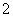 个红球,
个红球,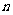 个白球.两甲,乙两袋中各任取
个白球.两甲,乙两袋中各任取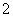 个球.
个球.
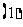 若
若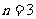 ,求取到的
,求取到的 个球全是红球的概率;
个球全是红球的概率;
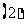 若取到的
若取到的 个球中至少有
个球中至少有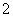 个红球的概率为
个红球的概率为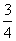 ,求
,求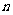 .
.

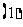 袋中有
袋中有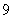 个编号为
个编号为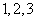 ,…,
,…,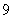 的小球,从中任意随机取出
的小球,从中任意随机取出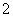 个,求至少有
个,求至少有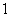 个编号为奇数的概率;
个编号为奇数的概率;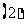 同时掷
同时掷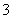 枚骰子时,求出现的点数的和是
枚骰子时,求出现的点数的和是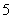 的倍数的概率.
的倍数的概率.
问题1.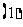 从装有
从装有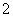 个红球和
个红球和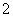 各白球的口袋中任取两个球,那么下列事件中互斥事件的个数是
各白球的口袋中任取两个球,那么下列事件中互斥事件的个数是 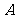
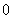 个
个 
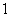 个
个 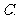
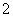 个
个 
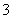 个
个
①至少有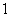 个白球,都是白球;②至少有
个白球,都是白球;②至少有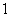 个白球,至少有
个白球,至少有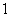 个红球;
个红球;
③恰有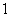 个白球,恰有
个白球,恰有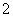 个白球;④至少有
个白球;④至少有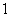 个白球,都是红球.
个白球,都是红球.
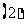 将一枚骰子向上抛掷一次,设事件
将一枚骰子向上抛掷一次,设事件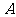 表示向上的一面出现奇数点,事件
表示向上的一面出现奇数点,事件 表示向上的一面出现的点数不超过
表示向上的一面出现的点数不超过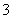 ,事件
,事件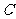 表示向上的一面出现的点数不少于
表示向上的一面出现的点数不少于 ,则
,则
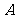
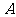 与
与 是互斥而非对立事件
是互斥而非对立事件 
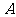 与
与 是对立事件
是对立事件
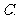
 与
与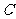 互斥而非对立事件
互斥而非对立事件

 与
与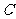
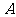 与
与 是对立事件
是对立事件
问题2.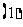 从分别写有
从分别写有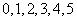 的六件卡片中,任取三张并组成三位数,计算:
的六件卡片中,任取三张并组成三位数,计算:
①这个三位数是偶数的概率;②这个三位数能被三整除的概率;③这个三位数比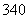 小的概率.
小的概率.
 (
( 天津)已知甲盒内有大小相同的
天津)已知甲盒内有大小相同的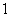 个红球和
个红球和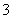 个黑球,乙盒内有大小相同的
个黑球,乙盒内有大小相同的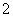 个红球和
个红球和 个黑球.现从甲、乙两个盒内各任取
个黑球.现从甲、乙两个盒内各任取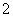 个球.
个球.
①略;②求取出的 个球中恰有
个球中恰有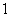 个红球的概率;③略.
个红球的概率;③略.
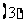 (
(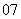 重庆)从
重庆)从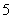 张
张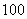 元,
元,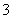 张
张 元,
元,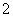 张
张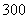 元的奥运预赛门票中任取
元的奥运预赛门票中任取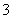 张,则所取
张,则所取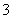 张中至少有
张中至少有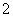 张价格相同的概率为
张价格相同的概率为
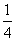

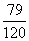
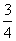


问题3.从男女生共有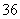 人的班中,选出两名代表,每人当选的机会均等,如果选的同性代表的概率是
人的班中,选出两名代表,每人当选的机会均等,如果选的同性代表的概率是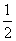 ,求该班中男女相差几名?
,求该班中男女相差几名?
问题4.( 全国Ⅱ文)从某批产品中,有放回地抽取产品二次,每次随机抽取
全国Ⅱ文)从某批产品中,有放回地抽取产品二次,每次随机抽取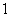 件,假设事件
件,假设事件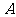 :“取出的
:“取出的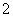 件产品中至多有
件产品中至多有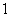 件是二等品”的概率
件是二等品”的概率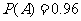 .
.
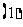 求从该批产品中任取
求从该批产品中任取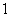 件是二等品的概率
件是二等品的概率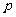 ;
;
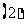 若该批产品共
若该批产品共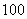 件,从中任意抽取
件,从中任意抽取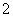 件,求事件
件,求事件 :“取出的
:“取出的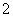 件产品中至少有一件二等品”的概率
件产品中至少有一件二等品”的概率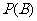 .
.
 互斥事件的概念:不可能同时发生的个事件叫做互斥事件.
互斥事件的概念:不可能同时发生的个事件叫做互斥事件.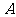 、
、 互斥,即事件
互斥,即事件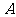 、
、 不可能同时发生,这时
不可能同时发生,这时 ,
,
一般地:如果事件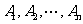 中的任何两个都是互斥的,那么就说事件
中的任何两个都是互斥的,那么就说事件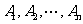 彼此互斥.
彼此互斥.
 对立事件的概念:事件
对立事件的概念:事件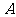 和事件
和事件 必有一个发生的互斥事件
必有一个发生的互斥事件
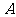 、
、 对立,即事件
对立,即事件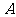 、
、 不可能同时发生,但
不可能同时发生,但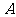 、
、 中必然有一个发生
中必然有一个发生 这时
这时 ,
,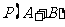

 ,一般地,
,一般地, .
.
 对于互斥事件要抓住如下的特征进行理解:
对于互斥事件要抓住如下的特征进行理解:
第一,互斥事件研究的是两个事件之间的关系;第二,所研究的两个事件是在一次试验中涉及的;第三,两个事件互斥是从试验的结果不能同时出现来确定的.
从集合角度来看,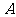 、
、 两个事件互斥,则表示
两个事件互斥,则表示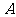 、
、 这两个事件所含结果组成的集合的交集是空集.
这两个事件所含结果组成的集合的交集是空集.
对立事件是互斥事件的一种特殊情况,是指在一次试验中有且仅有一个发生的两个事件,集合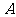 的对立事件记作
的对立事件记作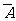 ,从集合的角度来看,事件
,从集合的角度来看,事件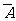 所含结果的集合正是全集
所含结果的集合正是全集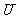 中由事件
中由事件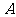 所含结果组成集合的补集,即
所含结果组成集合的补集,即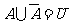 ,
,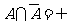 。对立事件一定是互斥事件,但互斥事件不一定是对立事件.
。对立事件一定是互斥事件,但互斥事件不一定是对立事件.
当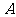 和
和 互斥时,事件
互斥时,事件 的概率满足加法公式:
的概率满足加法公式:
 (
(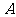 、
、 互斥)当计算事件
互斥)当计算事件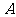 的概率
的概率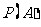 比较困难时,有时计算它的对立事件
比较困难时,有时计算它的对立事件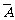 的概率则要容易些,为此有
的概率则要容易些,为此有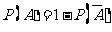 .
.
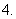 互斥事件的概率的求法:如果事件
互斥事件的概率的求法:如果事件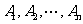 彼此互斥,那么
彼此互斥,那么
 =
= .
.
 分类讨论思想:分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.
分类讨论思想:分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.
 (
(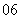 福建)在一个口袋中装有
福建)在一个口袋中装有 个白球和
个白球和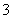 个黑球,这些球除颜色外完全相同.从中摸出
个黑球,这些球除颜色外完全相同.从中摸出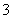 个球,至少摸到
个球,至少摸到 个黑球的概率等于
个黑球的概率等于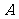
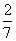

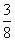
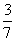
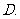
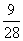
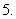 (
( 上海)两部不同的长篇小说各由第一、二、三、四卷组成,每卷
上海)两部不同的长篇小说各由第一、二、三、四卷组成,每卷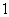 本,共
本,共 本.将它们任意地排成一排,左边
本.将它们任意地排成一排,左边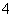 本恰好都属于同一部小说的概率是
(结果用分数表示).
本恰好都属于同一部小说的概率是
(结果用分数表示).
 (
( 重庆)某轻轨列车有
重庆)某轻轨列车有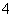 节车厢,现有
节车厢,现有 位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这
位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这 位乘客进入各节车厢的人数恰好为
位乘客进入各节车厢的人数恰好为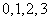 的概率为
的概率为
 (
( 湖北)以平行六面体
湖北)以平行六面体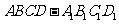 的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率
的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率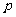 为
为
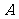
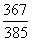

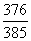
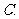
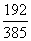
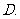
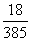
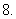 (
(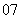 江西文)栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树成苗的概率分别为
江西文)栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树成苗的概率分别为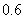 ,
,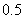 ,移栽后成活的概率分别为
,移栽后成活的概率分别为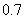 ,
, .
.
 求甲、乙两种果树至少有一种果树成苗的概率;
求甲、乙两种果树至少有一种果树成苗的概率;
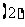 求恰好有一种果树能培育成苗且移栽成活的概率.
求恰好有一种果树能培育成苗且移栽成活的概率.
 (
( 北京文)某条公共汽车线路沿线共有
北京文)某条公共汽车线路沿线共有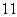 个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有
个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有 位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
 这
这 位乘客在其不相同的车站下车的概率;
位乘客在其不相同的车站下车的概率;
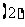 这
这 位乘客中恰有
位乘客中恰有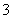 人在终点站下车的概率;
人在终点站下车的概率;
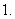 (
( 届高三成都名校联盟预测二)从单词“
届高三成都名校联盟预测二)从单词“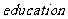 ”中选取
”中选取 个不同的字母排成
个不同的字母排成
一排,则含“ ”(“
”(“ ”相连且顺序不变)的概率为
”相连且顺序不变)的概率为
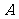
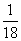


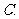
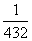
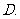

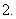 从分别写有
从分别写有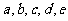 的五张卡片里任取两张,这两张卡片里的字母恰好是按照字母顺序相邻排列的概率等于
的五张卡片里任取两张,这两张卡片里的字母恰好是按照字母顺序相邻排列的概率等于 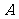


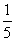
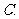
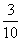
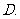
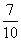
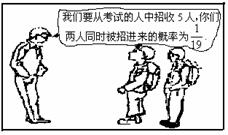
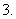 两位同学去某大学参加自主招生考试,根据
两位同学去某大学参加自主招生考试,根据
右图学校负责人与他们两人的对话,可推断
出参加考试的人数为
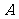
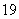
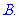
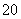
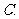
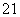
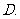
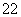
问题1.一个口袋内装有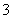 个白球和
个白球和 个红球,从中任意取出一个球.
个红球,从中任意取出一个球.
 “取出的球是黑球”是什么事件?它的概率是多少?
“取出的球是黑球”是什么事件?它的概率是多少?
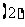 “取出的球是红球”是什么事件?它的概率是多少?
“取出的球是红球”是什么事件?它的概率是多少?
 “取出的球是白球或红”是什么事件?它的概率是多少?
“取出的球是白球或红”是什么事件?它的概率是多少?
问题2.(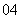 天津)从
天津)从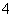 名男生和
名男生和 名女生中任选
名女生中任选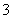 人参加演讲比赛.
人参加演讲比赛.
 求所选
求所选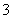 人都是男生的概率;
人都是男生的概率;
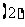 求所选
求所选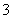 人中恰有
人中恰有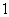 名女生的概率;
名女生的概率;
 求所选
求所选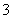 人中至少有
人中至少有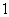 名女生的概率.
名女生的概率.
问题3. (
( 上海)在五个数字
上海)在五个数字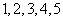 中,若随机取出三个数字,则剩下两个数字都是奇数的概率是 (结果用数值表示).
中,若随机取出三个数字,则剩下两个数字都是奇数的概率是 (结果用数值表示).
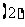 (
(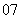 辽宁)一个坛子里有编号为
辽宁)一个坛子里有编号为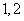 ,…,
,…,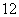 的
的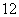 个大小相同的球,其中
个大小相同的球,其中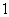 到
到 号球是红球,其余的是黑球,若从中任取两个球,则取到的都是红球,且至少有
号球是红球,其余的是黑球,若从中任取两个球,则取到的都是红球,且至少有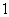 个球的号码是偶数的概率是
个球的号码是偶数的概率是 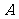
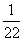

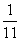
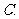

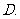

 (
(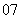 湖北文)将
湖北文)将 本不同的书全发给
本不同的书全发给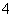 名同学,每名同学至少有一本书的概率是
名同学,每名同学至少有一本书的概率是
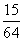


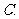
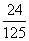
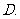
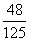
问题4. (
(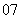 安徽文)在正方体上任意选择两条棱,则这两条棱相互平行的概率为
安徽文)在正方体上任意选择两条棱,则这两条棱相互平行的概率为
 (
(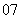 江西)将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为
江西)将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为
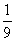

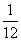

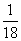
 (
( 湖北)连掷两次骰子得到的点数分别为
湖北)连掷两次骰子得到的点数分别为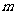 和
和 ,记向量
,记向量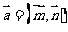 与向量
与向量 的夹角为
的夹角为 ,则
,则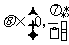 的概率是
的概率是 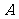


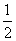
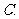
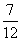
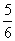
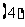 (
(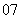 江西文)一袋中装有大小相同,编号分别为
江西文)一袋中装有大小相同,编号分别为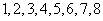 的八个球,从中有放回地每次取一个球,共取
的八个球,从中有放回地每次取一个球,共取 次,则取得两个球的编号和不小于
次,则取得两个球的编号和不小于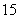 的概率为
的概率为
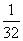

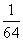
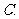

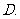
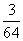
 (
( 四川)已知一组抛物线
四川)已知一组抛物线 ,其中
,其中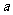 为
为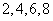 中任取的一个数,
中任取的一个数,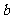 为
为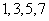 中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线
中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线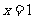 交点处的切线相互平行的概率是
交点处的切线相互平行的概率是 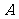
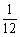

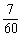
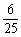
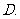
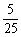
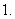 事件的定义:
事件的定义:
随机事件:在一定条件下可能发生也可能不发生的事件;必然事件:在一定条件下必然发生的事件;不可能事件:在一定条件下不可能发生的事件.
 随机事件的概率:一般地,在大量重复进行同一试验时,事件
随机事件的概率:一般地,在大量重复进行同一试验时,事件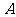 发生的频率
发生的频率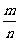 总是接近某个常数,在它附近摆动,这时就把这个常数叫做事件
总是接近某个常数,在它附近摆动,这时就把这个常数叫做事件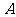 的概率,记作
的概率,记作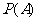 .
.
 概率的确定方法:通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率;
概率的确定方法:通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率;
 概率的性质:必然事件的概率为
概率的性质:必然事件的概率为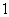 ,不可能事件的概率为
,不可能事件的概率为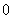 ,随机事件的概率为
,随机事件的概率为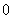 ≤
≤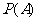 ≤
≤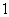 ,必然事件和不可能事件看作随机事件的两个极端情形.
,必然事件和不可能事件看作随机事件的两个极端情形.
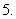 基本事件:一次试验连同其中可能出现的每一个结果(事件
基本事件:一次试验连同其中可能出现的每一个结果(事件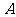 )称为一个基本事件.
)称为一个基本事件.
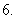 等可能性事件:如果一次试验中可能出现的结果有
等可能性事件:如果一次试验中可能出现的结果有 个,而且所有结果出现的可能性都相等,那么每个基本事件的概率都是
个,而且所有结果出现的可能性都相等,那么每个基本事件的概率都是 ,这种事件叫等可能性事件.
,这种事件叫等可能性事件.
 等可能性事件的概率:如果一次试验中可能出现的结果有
等可能性事件的概率:如果一次试验中可能出现的结果有 个,而且所有结果都是等可能的,如果事件
个,而且所有结果都是等可能的,如果事件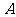 包含
包含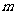 个结果,那么事件
个结果,那么事件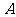 的概率
的概率 .
.
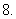 随机事件的概率、等可能事件的概率计算
随机事件的概率、等可能事件的概率计算
首先、对于每一个随机实验来说,可能出现的实验结果是有限的;其次、所有不同的实验结果的出现是等可能的.一定要在等可能的前提下计算基本事件的个数.只有在每一种可能出现的概率都相同的前提下,计算出的基本事件的个数才是正确的,才能用等可能事件的概率计算公式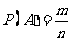 来进行计算.
来进行计算.
 等可能性事件的概率公式及一般求解方法.求解等可能性事件
等可能性事件的概率公式及一般求解方法.求解等可能性事件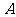 的概率一般遵循如下步骤:
的概率一般遵循如下步骤: 先确定一次试验是什么,此时一次试验的可能性结果有多少,即求出
先确定一次试验是什么,此时一次试验的可能性结果有多少,即求出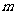 .
.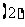 再确定所研究的事件
再确定所研究的事件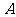 是什么,事件
是什么,事件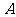 包括结果有多少,即求出
包括结果有多少,即求出 ,
, 应用等可能性事件概率公式
应用等可能性事件概率公式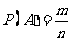 计算,也可从不同的背景材料抽象出两个问题:(ⅰ)所有基本事件的个数,即
计算,也可从不同的背景材料抽象出两个问题:(ⅰ)所有基本事件的个数,即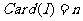 ,(ⅱ)事件
,(ⅱ)事件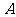 包含的基本事件的个数,即
包含的基本事件的个数,即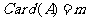 ,最后套用公式
,最后套用公式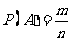 .确定
.确定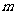 、
、 的数值是关键所在,其计算方法灵活多变,没有固定的模式,可充分利用排列组合知识中的分类计数原理和分步计数原理,必须做到不重复不遗漏.
的数值是关键所在,其计算方法灵活多变,没有固定的模式,可充分利用排列组合知识中的分类计数原理和分步计数原理,必须做到不重复不遗漏.
 放回抽样与不妨回抽样是等可能事件概率的两种重要模型,其中摸球问题、次品检验问题是经常出现的试题形式,解题时要注意抽样有无放回.
放回抽样与不妨回抽样是等可能事件概率的两种重要模型,其中摸球问题、次品检验问题是经常出现的试题形式,解题时要注意抽样有无放回.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com