
(一)下列四国局部图中的A、B、C、D为各国重要海港,读图回答1-3题。
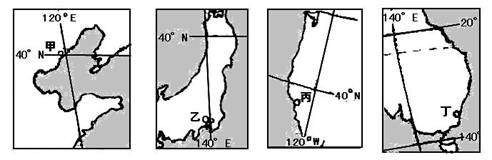
1.甲港口主要输出的物资是 ( )
A.粮食 B.煤炭 C.木材 D.铁矿石
2.丙港与丁港相比 ( )
A.沿岸都为暖流流经 B.高温期一致
C.沿岸都为寒流流经 D.多雨期一致
3.有关四国间贸易的叙述,正确的是 ( )
A.甲所在国从乙所在国进口铁矿石 B.丁所在国从甲所在国进口煤炭
C.乙所在国出口小汽车到丙所在国 D.丙所在国出口石油到乙所在国
每小题只有1个正确答案,将代表正确答案的字母填入相应的空格内。
1 已知函数y=Asin(ωx+φ)在一个周期内,当x=
已知函数y=Asin(ωx+φ)在一个周期内,当x=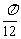 时,取得最大值2,当x=
时,取得最大值2,当x=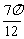 时取得最小值-2,那么( )
时取得最小值-2,那么( )

 2
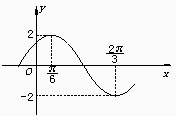
2 如图,已知函数y=Asin(ωx+φ)的图象(的部分),则函数的表达式为( )
如图,已知函数y=Asin(ωx+φ)的图象(的部分),则函数的表达式为( )
A y=2sin(
y=2sin(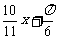 )
)
B y=2sin(
y=2sin(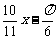 )
)
C y=2sin(2x+
y=2sin(2x+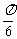 )
)
D y=2sin(2x-
y=2sin(2x-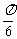 )
)
3 函数y=2sin(
函数y=2sin(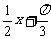 )在一个周期内的三个“零点”横坐标是( )
)在一个周期内的三个“零点”横坐标是( )

4 函数y=|sin(ωx-2)|(ω>0)的周期为2,则ω=
函数y=|sin(ωx-2)|(ω>0)的周期为2,则ω= 
5 若函数y=asinx+b(a<0
若函数y=asinx+b(a<0 的最小值为-
的最小值为-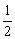 ,最大值为
,最大值为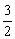 ,则a、b的值分别为________
,则a、b的值分别为________
6 函数y=3sin(2x+φ)(0<φ<π
函数y=3sin(2x+φ)(0<φ<π 为偶函数,则φ=
为偶函数,则φ= 
1 (1)y=sin(x+
(1)y=sin(x+ )是由y=sinx向左平移
)是由y=sinx向左平移 个单位得到的
个单位得到的
(2)y=sin(x- )是由y=sinx向右平移
)是由y=sinx向右平移 个单位得到的
个单位得到的
(3)y=sin(x- )是由y=sin(x+
)是由y=sin(x+ )向右平移
)向右平移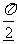 个单位得到的
个单位得到的
2 若将某函数的图象向右平移
若将某函数的图象向右平移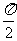 以后所得到的图象的函数式是y=sin(x+
以后所得到的图象的函数式是y=sin(x+ ),则原来的函数表达式为( )
),则原来的函数表达式为( )
A y=sin(x+
y=sin(x+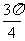 )
B
)
B y=sin(x+
y=sin(x+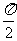 )
)
C y=sin(x-
y=sin(x- )
D
)
D y=sin(x+
y=sin(x+ )-
)-
答案:A
3 把函数y=cos(3x+
把函数y=cos(3x+ )的图象适当变动就可以得到y=sin(-3x)的图象,这种变动可以是( )
)的图象适当变动就可以得到y=sin(-3x)的图象,这种变动可以是( )
A 向右平移
向右平移 B
B 向左平移
向左平移 C
C 向右平移
向右平移 D
D 向左平移
向左平移
分析:三角函数图象变换问题的常规题型是:已知函数和变换方法,求变换后的函数或图象,此题是已知变换前后的函数,求变换方式的逆向型题目,解题的思路是将异名函数化为同名函数,且须x的系数相同
解:∵y=cos(3x+ )=sin(
)=sin( -3x)=sin[-3(x-
-3x)=sin[-3(x- )]
)]
∴由y=sin[-3(x- )]向左平移
)]向左平移 才能得到y=sin(-3x)的图象
才能得到y=sin(-3x)的图象
答案:D
4 将函数y=f(x)的图象沿x轴向右平移
将函数y=f(x)的图象沿x轴向右平移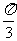 ,再保持图象上的纵坐标不变,而横坐标变为原来的2倍,得到的曲线与y=sinx的图象相同,则y=f(x)是( )
,再保持图象上的纵坐标不变,而横坐标变为原来的2倍,得到的曲线与y=sinx的图象相同,则y=f(x)是( )
A y=sin(2x+
y=sin(2x+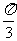 )
B
)
B y=sin(2x-
y=sin(2x-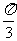 )
)
C y=sin(2x+
y=sin(2x+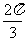 )
D
)
D y=sin(2x-
y=sin(2x-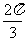 )
)
分析:这是三角图象变换问题的又一类逆向型题,解题的思路是逆推法
解:y=f(x)可由y=sinx,纵坐标不变,横坐标压缩为原来的1/2,得y=sin2x;再沿x轴向左平移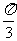 得y=sin2(x+
得y=sin2(x+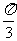 ),即f(x)=sin(2x+
),即f(x)=sin(2x+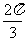 )
)
答案:C
5 若函数f(x)=sin2x+acos2x的图象关于直线x=-
若函数f(x)=sin2x+acos2x的图象关于直线x=-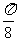 对称,则a=–1
对称,则a=–1
分析:这是已知函数图象的对称轴方程,求函数解析式中参数值的一类逆向型题,解题的关键是如何巧用对称性
解:∵x1=0,x2=- 是定义域中关于x=-
是定义域中关于x=-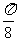 对称的两点
对称的两点
∴f(0)=f(- )
)
即0+a=sin(-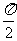 )+acos(-
)+acos(-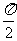 )
)
∴a=-1
6 若对任意实数a,函数y=5sin(
若对任意实数a,函数y=5sin(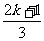 πx-
πx-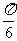 )(k∈N)在区间[a,a+3]上的值
)(k∈N)在区间[a,a+3]上的值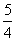 出现不少于4次且不多于8次,则k的值是( )
出现不少于4次且不多于8次,则k的值是( )
A 2 B
2 B 4 C
4 C 3或4 D
3或4 D 2或3
2或3
分析:这也是求函数解析式中参数值的逆向型题,解题的思路是:先求出与k相关的周期T的取值范围,再求k
解:∵T=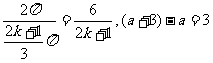
又因每一周期内出现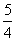 值时有2次,出现4次取2个周期,出现
值时有2次,出现4次取2个周期,出现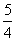 值8次应有4个周期
值8次应有4个周期
∴有4T≥3且2T≤3
即得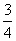 ≤T≤
≤T≤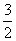 ,∴
,∴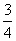 ≤
≤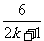 ≤
≤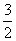
解得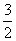 ≤k≤
≤k≤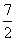 ,∵k∈N,∴k=2或3
,∵k∈N,∴k=2或3
答案:D
例 画出函数
y=sin(x+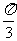 ),x∈R
),x∈R
y=sin(x- ),x∈R
),x∈R
的简图
解:列表
|
x |
-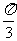 |
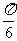 |
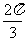 |
 |
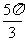 |
x+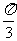 |
0 |
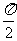 |
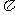 |
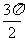 |
2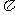 |
sin(x+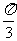 ) ) |
0 |
1 |
0 |
–1 |
0 |
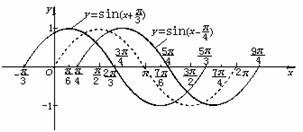
描点画图:
|
x |
 |
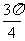 |
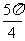 |
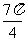 |
 |
x- |
0 |
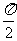 |
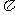 |
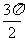 |
2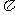 |
sin(x– ) ) |
0 |
1 |
0 |
–1 |
0 |
通过比较,发现:
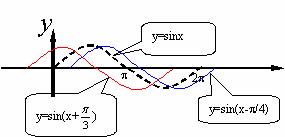
(1)函数y=sin(x+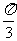 ),x∈R的图象可看作把正弦曲线上所有的点向左平行移动
),x∈R的图象可看作把正弦曲线上所有的点向左平行移动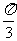 个单位长度而得到
个单位长度而得到
(2)函数y=sin(x- ),x∈R的图象可看作把正弦曲线上所有点向右平行移动
),x∈R的图象可看作把正弦曲线上所有点向右平行移动 个单位长度而得到
个单位长度而得到
一般地,函数y=sin(x+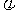 ),x∈R(其中
),x∈R(其中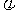 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当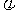 >0时)或向右(当
>0时)或向右(当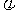 <0时=平行移动|
<0时=平行移动|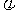 |个单位长度而得到
|个单位长度而得到 (用平移法注意讲清方向:“加左”“减右”)
(用平移法注意讲清方向:“加左”“减右”)
y=sin(x+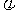 )与y=sinx的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
)与y=sinx的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
2.周期变换:函数y=sinωx, xÎR (ω>0且ω¹1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的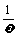 倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图
倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图 ω决定了函数的周期
ω决定了函数的周期
我们随着学习三角函数的深入,还会遇到形如y=sin(x+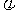 )的三角函数,这种函数的图象又该如何得到呢?今天,我们一起来探讨一下
)的三角函数,这种函数的图象又该如何得到呢?今天,我们一起来探讨一下
1.振幅变换:y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的 它的值域[-A, A] 最大值是A, 最小值是-A.若A<0 可先作y=-Asinx的图象 ,再以x轴为对称轴翻折
它的值域[-A, A] 最大值是A, 最小值是-A.若A<0 可先作y=-Asinx的图象 ,再以x轴为对称轴翻折 A称为振幅
A称为振幅
20.在直角坐标系 中,点P到两点
中,点P到两点 ,
,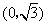 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为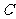 ,直线
,直线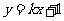 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;(Ⅱ)若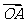
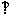
 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|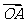 |>|
|>| |.
|.
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以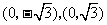 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴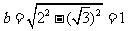 ,故方程为
,故方程为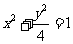 .
.
(Ⅱ)设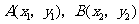 ,其坐标满足
,其坐标满足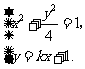
消去y并整理得 ,
,
故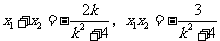 .若
.若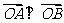 ,即
,即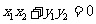 .
.
而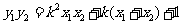 ,于是
,于是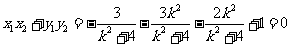 ,
,
化简得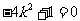 ,所以
,所以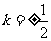 .
.
(Ⅲ)

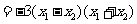
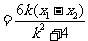 .
.
因为A在第一象限,故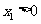 .由
.由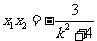 知
知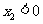 ,从而
,从而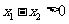 .又
.又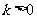 ,
,
故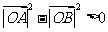 ,即在题设条件下,恒有
,即在题设条件下,恒有 .
.
19.已知菱形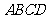 顶点
顶点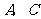 在椭圆
在椭圆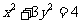 上,对角线
上,对角线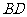 的斜率为1.
的斜率为1.
(Ⅰ)当直线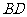 过点
过点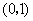 时,求直线
时,求直线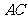 的方程;
的方程;
(Ⅱ)当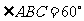 时,求菱形
时,求菱形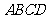 面积的最大值.
面积的最大值.
解:(Ⅰ)由题意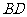 的方程为
的方程为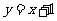 .因四边形
.因四边形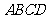 为菱形,所以
为菱形,所以 .
.
于是可设直线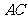 的方程为
的方程为 .由
.由 得
得 .
.
因为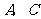 在椭圆上,所以
在椭圆上,所以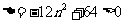 ,解得
,解得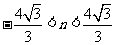 .
.
设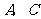 两点坐标分别为
两点坐标分别为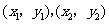 ,则
,则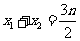 ,
,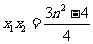 ,
, ,
, .所以
.所以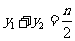 .所以
.所以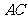 的中点坐标为
的中点坐标为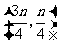 .
.
由四边形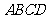 为菱形可知,点
为菱形可知,点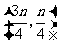 在直线
在直线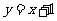 上,
上,
所以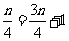 ,解得
,解得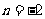 .所以直线
.所以直线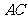 的方程为
的方程为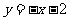 ,即
,即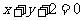 .
.
(Ⅱ)因为四边形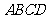 为菱形,且
为菱形,且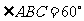 ,
,
所以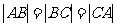 .所以菱形
.所以菱形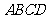 的面积
的面积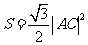 .由(Ⅰ)
.由(Ⅰ)
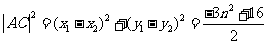 ,
,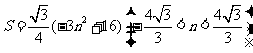 .
.
所以当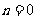 时,菱形
时,菱形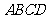 的面积取得最大值
的面积取得最大值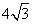 .
.
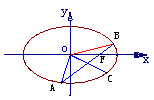
18.如图 ,椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A、B两点, 若椭圆上存在一点C, 使 +
+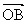 =
=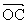 .
.
(1) 求椭圆的离心率;(2) 若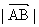 =15, 求着个椭圆的方程.
=15, 求着个椭圆的方程.
 解: (1)设椭圆的方程为
解: (1)设椭圆的方程为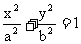 , 焦距为
, 焦距为 , 则直线l的方程为:
, 则直线l的方程为: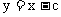 ,
,
代入椭圆方程, 得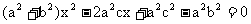 ,
,
设点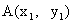 、
、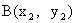 ,
,
则
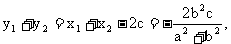
∵ +
+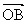
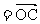 , ∴C点坐标为
, ∴C点坐标为 .
.
∵C点在椭圆上, ∴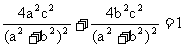 .∴
.∴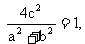
∴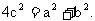 又
又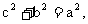 ∴
∴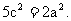 ∴
∴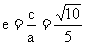
(2) ∵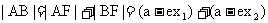
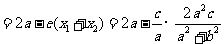
 由已知
由已知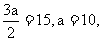 从而
从而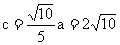 .
.
∴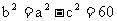 .故椭圆的方程为:
.故椭圆的方程为: 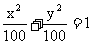 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com