
8.(2008·武汉模拟)下图是北朝后期佛教信徒人数比例变化示意图,读图指出造成这种变化的社会根源是 ( )
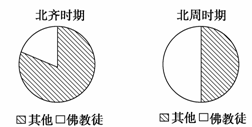
A.南北朝时期战乱频繁 B.统治者对佛教的重视
C.名僧致力于传教 D.佛教有强烈的欺骗性
答案 A
7.(2008·廊坊模拟) 右图是一南朝时期的青釉莲花瓣托碗,以下四种说法,正确的是 ( )
 A.它制作精细,不是国内所产
A.它制作精细,不是国内所产
B.它属于青瓷,因此产地是在南方
C.它属于青瓷,因此产地是在北方
D.它属于白瓷,因为它的产地在南方
答案 B
6.两晋南北朝时期,中原农耕规模出现缩小现象,而畜牧业有所扩展,造成这一现象的直接原因是 ( )
A.生产技术落后 B.自然条件恶化
C.少数民族重牧轻农 D.战乱频繁
答案 C
5.从人与自然的角度看,魏晋南北朝时期北方的发展状况是 ( )
A.环境状况恶化 B.环境状况良好
C.环境破坏缓解 D.环境破坏加剧
答案 C
4.(2009·济宁模拟) 魏晋南北朝时期,我国经济发展的突出特点是 ( )
A.寺院经济占主导地位 B.北方经济发展较快
C.南北经济发展趋于平衡 D.经济重心开始南移
答案 C
3.北方劳动人民南迁对南方生产发展最直接的影响在于 ( )
①充实了江南劳动力 ②带去了先进的生产技术 ③导致南方人观念更新 ④促进了民族之间的融合
A.①② B.②③ C.①④ D.①③
答案 A
2.(2007·江苏)东晋南朝时期,江南经济迅速发展,乃至有“江南之为国盛矣”的赞叹。该时期江南开发的主要因素不包括 ( )
A.北方大量人口南迁 B.民族融合进一步加强
C.统治者推行劝课农桑等政策 D.农产品商品化程度高
答案 D
1.下图中,东晋南朝经济开发成就最突出的地区是 ( )

A.① B.② C.③ D.④
答案 C
例1:定义在R上的非常数函数满足:f (10+x)为偶函数,且f (5-x) = f (5+x),则f (x)一定是( ) (第十二届希望杯高二 第二试题)
(A)是偶函数,也是周期函数 (B)是偶函数,但不是周期函数
(C)是奇函数,也是周期函数 (D)是奇函数,但不是周期函数
解:∵f (10+x)为偶函数,∴f (10+x) = f (10-x).
∴f (x)有两条对称轴 x = 5与x =10 ,因此f (x)是以10为其一个周期的周期函数, ∴x =0即y轴也是f (x)的对称轴,因此f (x)还是一个偶函数。
故选(A)
例2:设定义域为R的函数y = f (x)、y = g(x)都有反函数,并且f(x-1)和g-1(x-2)函数的图像关于直线y = x对称,若g(5) = 1999,那么f(4)=( )。
(A) 1999; (B)2000; (C)2001; (D)2002。
解:∵y = f(x-1)和y = g-1(x-2)函数的图像关于直线y = x对称,
∴y = g-1(x-2) 反函数是y = f(x-1),而y = g-1(x-2)的反函数是:y = 2 + g(x), ∴f(x-1) = 2 + g(x), ∴有f(5-1) = 2 + g(5)=2001
故f(4) = 2001,应选(C)
例3.设f(x)是定义在R上的偶函数,且f(1+x)= f(1-x),当-1≤x≤0时,
f (x) = -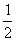 x,则f (8.6 ) = _________
(第八届希望杯高二 第一试题)
x,则f (8.6 ) = _________
(第八届希望杯高二 第一试题)
解:∵f(x)是定义在R上的偶函数∴x = 0是y = f(x)对称轴;
又∵f(1+x)= f(1-x) ∴x = 1也是y = f (x) 对称轴。故y = f(x)是以2为周期的周期函数,∴f (8.6 ) = f (8+0.6 ) = f (0.6 ) = f (-0.6 ) = 0.3
例4.函数 y = sin (2x + 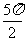 )的图像的一条对称轴的方程是( )(92全国高考理) (A) x = -
)的图像的一条对称轴的方程是( )(92全国高考理) (A) x = - (B) x = -
(B) x = -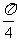 (C) x =
(C) x = 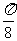 (D)
x =
(D)
x =
解:函数 y = sin (2x + 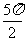 )的图像的所有对称轴的方程是2x +
)的图像的所有对称轴的方程是2x + 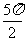 = k
= k +
+
∴x =  -
-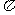 ,显然取k = 1时的对称轴方程是x = -
,显然取k = 1时的对称轴方程是x = - 故选(A)
故选(A)
例5. 设f(x)是定义在R上的奇函数,且f(x+2)= -f(x),当0≤x≤1时,
f (x) = x,则f (7.5 ) = ( )
(A) 0.5 (B) -0.5 (C) 1.5 (D) -1.5
解:∵y = f (x)是定义在R上的奇函数,∴点(0,0)是其对称中心;
又∵f (x+2 )= -f (x) = f (-x),即f (1+ x) = f (1-x), ∴直线x = 1是y = f (x) 对称轴,故y = f (x)是周期为2的周期函数。
∴f (7.5 ) = f (8-0.5 ) = f (-0.5 ) = -f (0.5 ) =-0.5 故选(B)
|
函 数 |
对称中心坐标 |
对称轴方程 |
|
y = sin x |
( kπ, 0 ) |
x = kπ+π/2 |
|
y = cos x |
( kπ+π/2 ,0 ) |
x = kπ |
|
y = tan x |
(kπ/2 ,0 ) |
无 |
注:①上表中k∈Z
②y = tan x的所有对称中心坐标应该是(kπ/2 ,0 ),而在岑申、王而冶主编的浙江教育出版社出版的21世纪高中数学精编第一册(下)及陈兆镇主编的广西师大出版社出版的高一数学新教案(修订版)中都认为y = tan x的所有对称中心坐标是( kπ, 0 ),这明显是错的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com