

2. (上海虹口区08学年高三数学第一学期期末试卷16)在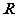 上定义运算:
上定义运算: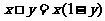 ,若不等式
,若不等式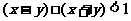 对一切实数
对一切实数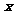 恒成立,则实数
恒成立,则实数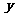 的取值范围是
( )
的取值范围是
( )
A. 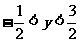 B.
B.  C.
C. 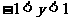 D.
D. 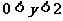
答案:A
1.(08年上海市部分重点中学高三联考13)如果a,b,c满足c<b<a且ac<0,那么下列选项中不一定成立的是 ---------- ( )
A. ab>ac B. c(b-a)>0 C. 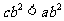 D. ac(a-c)<0
D. ac(a-c)<0
答案:C
17.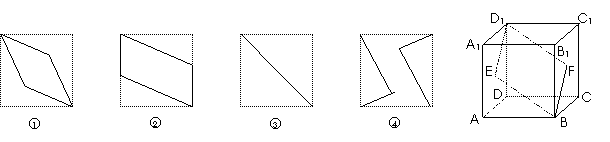 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
18 直线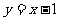 被抛物线
被抛物线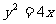 截得线段的中点坐标是___________.
截得线段的中点坐标是___________.
讲解 由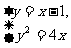 消去y,化简得
消去y,化简得
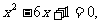
设此方程二根为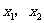 ,所截线段的中点坐标为
,所截线段的中点坐标为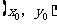 ,则
,则
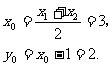
故 应填 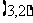 .
.
19 椭圆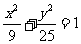 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解 记椭圆的二焦点为 ,有
,有
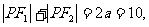
则知
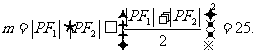
显然当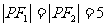 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填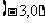 或
或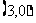
20 一只酒杯的轴截面是抛物线的一部分,它的函数解析式是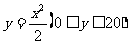 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
讲解 依抛物线的对称性可知,大圆的圆心在y轴上,并且圆与抛物线切于抛物线的顶点,从而可设大圆的方程为 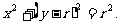
由

消去x,得 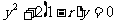 (*)
(*)
解出 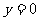 或
或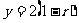
要使(*)式有且只有一个实数根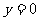 ,只要且只需要
,只要且只需要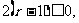 即
即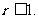
再结合半径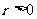 ,故应填
,故应填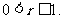
16. 若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是 (只需写出一个可能的值).
讲解 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
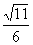 ,
,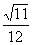 ,
,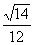 ,故应填.
,故应填.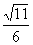 、
、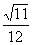 、
、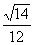 中的一个即可.
中的一个即可.
15. 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径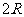 , 即有
, 即有
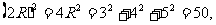
从而 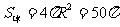 ,故应填
,故应填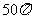
14. 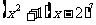 的展开式中
的展开式中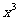 的系数是
的系数是
讲解 由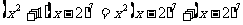 知,所求系数应为
知,所求系数应为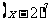 的x项的系数与
的x项的系数与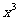 项的系数的和,即有
项的系数的和,即有
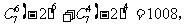
故应填1008.
13.某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
讲解 中奖号码的排列方法是: 奇位数字上排不同的奇数有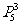 种方法,偶位数字上排偶数的方法有
种方法,偶位数字上排偶数的方法有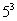 ,从而中奖号码共有
,从而中奖号码共有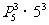 种,于是中奖面为
种,于是中奖面为
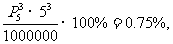
故应填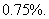
12.以下四个命题:
①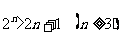
②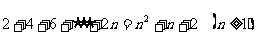
③凸n边形内角和为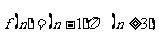 ④凸n边形对角线的条数是
④凸n边形对角线的条数是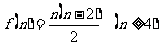
其中满足“假设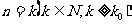 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当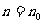 (
(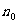 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时,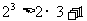 ,不等式成立;
,不等式成立;
② 当n=1时,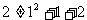 ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
 ;
;
③ 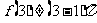 ,但假设
,但假设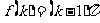 成立,则
成立,则
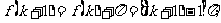
④ 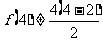 ,假设
,假设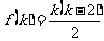 成立,则
成立,则

故应填②③.
11.
列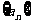 中,
中,
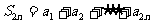 , 则
, 则
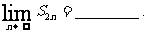

讲解 分类求和,得
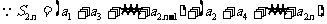

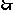
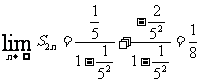 ,故应填
,故应填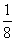 .
.
10. 已知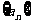 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果 是
是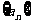 的前n项和,那么
的前n项和,那么
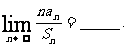

讲解 特别取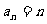 ,有
,有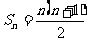 ,于是有
,于是有
 故应填2.
故应填2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com