
1. 解:设新电价为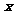 元/千瓦时
元/千瓦时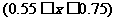 ,则新增用电量为
,则新增用电量为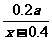 千瓦时.
千瓦时.
依题意,有
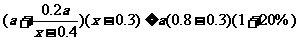 ,
,
即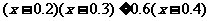 ,
,
整理,得
解此不等式,得 或
或 ,
,
又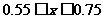 ,
,
所以,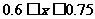 ,
,
因此,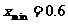 ,即电价最低为
,即电价最低为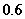 元/千瓦时,可保证电力部门的收益比上一年度至少增加20%.
元/千瓦时,可保证电力部门的收益比上一年度至少增加20%.
1(上海市卢湾区2008学年高三年级第一次质量调研第16题)(本题满分10分)
解不等式: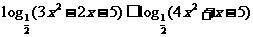 .
.
答案:解:原不等式的解集为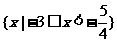
2 (2008学年度第一学期上海市普陀区高三年级质量调研第17题)(本题满分14分,第1小题6分,第2小题8分)
已知关于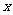 的不等式
的不等式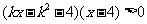 ,其中
,其中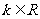 .
.
(1)
当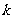 变化时,试求不等式的解集
变化时,试求不等式的解集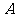 ;
;
(2)
对于不等式的解集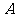 ,若满足
,若满足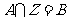 (其中
(其中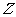 为整数集). 试探究集合
为整数集). 试探究集合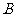 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合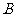 中元素个数最少的
中元素个数最少的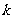 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合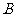 ;若不能,请说明理由.
;若不能,请说明理由.
答案:
解:(1)当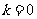 时,
时, ;
;
当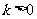 且
且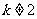 时,
时,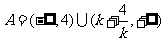 ;
;
当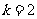 时,
时,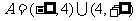 ;(不单独分析
;(不单独分析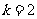 时的情况不扣分)
时的情况不扣分)
当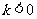 时,
时, .
.
(2)
由(1)知:当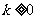 时,集合
时,集合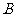 中的元素的个数无限;
中的元素的个数无限;
当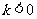 时,集合
时,集合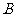 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合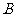 为有限集.
为有限集.
因为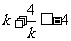 ,当且仅当
,当且仅当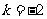 时取等号,
时取等号,
所以当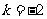 时,集合
时,集合 的元素个数最少.
的元素个数最少.
此时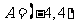 ,故集合
,故集合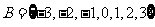 .
.
3 (静安区部分中学08-09学年度第一学期期中数学卷第19题)(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
某商品每件成本价80元,售价100元,每天售出100件.若售价降低x成(1成=10%),售出商品数量就增加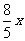 成,要求售价不能低于成本价.
成,要求售价不能低于成本价.
(1)设该商店一天的营业额为y,试求y与x之间的函数关系式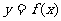 ,并写出定义域;
,并写出定义域;
(2)若再要求该商品一天营业额至少10260元,求x的取值范围.
答案:(1)依题意,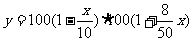 ;3分
;3分
又售价不能低于成本价,所以 .2分
.2分
所以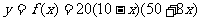 ,定义域为
,定义域为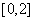 .2分
.2分
(2)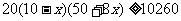 ,化简得:
,化简得: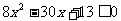 3分
3分
解得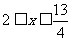 .3分
.3分
所以x的取值范围是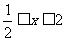 .1分
.1分
4 (静安区部分中学08-09学年度第一学期期中数学卷第20题)(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数 .
.
(1)(理)设集合 ,
,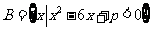 ,若
,若 ,求实数
,求实数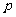 的取值范围;
的取值范围;
(文)若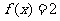 ,求
,求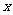 的值;
的值;
(2)若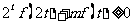 对于
对于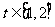 恒成立,求实数
恒成立,求实数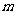 的取值范围.
的取值范围.
答案:(1)(理)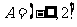 3分
3分
设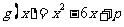 ,因为
,因为 ,所以
,所以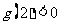
进而 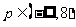 5分
5分
(文)(1)当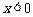 时,
时,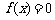 ;当
;当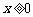 时,
时,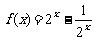 . ……
2分
. ……
2分
由条件可知 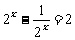 ,即
,即 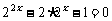 ,
,
解得 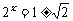 .
…… 4分
.
…… 4分
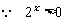 ,
, .
…… 2分
.
…… 2分
(2)因为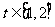 ,所以
,所以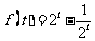 ,
2分
,
2分
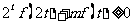 恒成立即
恒成立即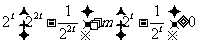 恒成立,
恒成立,
即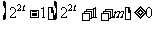 ,
,
因为 ,所以
,所以 恒成立,
3分
恒成立,
3分
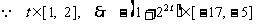 ,
,
即 3分
3分
5 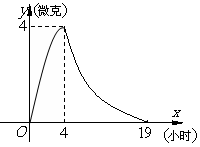 某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量
某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量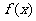 与时间
与时间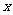 之间满足如图所示曲线.当
之间满足如图所示曲线.当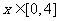 时,所示的曲线是二次函数图像的一部分,满足
时,所示的曲线是二次函数图像的一部分,满足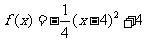 ,当
,当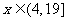 时,所示的曲线是函数
时,所示的曲线是函数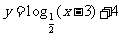 的图像的一部分.据测定:每毫升血液中含药量不少于
的图像的一部分.据测定:每毫升血液中含药量不少于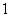 微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到
微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到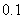 小时)
小时)
答案:由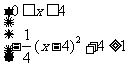 ,解得:
,解得: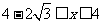 ①
(4分)
①
(4分)
由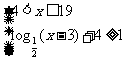 ,解得:
,解得: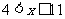 ②
(8分)
②
(8分)
由①、②知: , (10分)
, (10分)

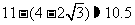 ,
(12分)
,
(12分)
∴服用这种药一次大概能维持的有效时间为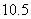 小时.
(14分)
小时.
(14分)
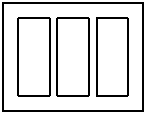
6 (上海市青浦区2008学年高三年级第一次质量调研第19题)(本题满分14分)
迎世博,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为 ,四周空白的宽度为
,四周空白的宽度为 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.
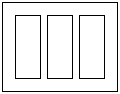
答案:解:设矩形栏目的高为 ,宽为
,宽为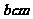 ,则
,则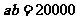 ,
,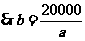
 广告的高为
广告的高为 ,宽为
,宽为 (其中
(其中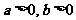 )
)
广告的面积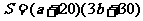
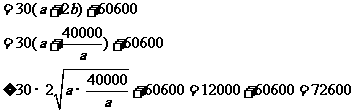
当且仅当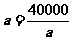 ,即
,即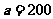 时,取等号,此时
时,取等号,此时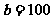 .
.
故当广告的高为200cm,宽为100cm时,可使广告的面积最小.
1.(上海市黄浦区2008学年高三年级第一次质量调研19)(本题满分12分)
某城市上年度电价为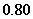 元/千瓦时,年用电量为
元/千瓦时,年用电量为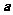 千瓦时.本年度计划将电价降到
千瓦时.本年度计划将电价降到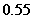 元/千瓦时-
元/千瓦时-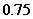 元/千瓦时之间,而居民用户期望电价为
元/千瓦时之间,而居民用户期望电价为 元/千瓦时(该市电力成本价为
元/千瓦时(该市电力成本价为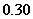 元/千瓦时)
元/千瓦时)
经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为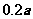 .试问当地电价最低为多少时,可保证电力部门的收益比上年度至少增加
.试问当地电价最低为多少时,可保证电力部门的收益比上年度至少增加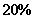 .
.
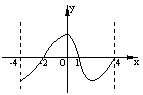
16. ( (上海市青浦区2008学年高三年级第一次质量调研第11题) 设函数 的定义域为
的定义域为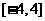 ,其图像如下图,那么不等式
,其图像如下图,那么不等式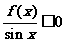 的解集为____________.答案:
的解集为____________.答案: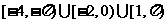
15. (浦东新区2008学年度第一学期期末质量抽测卷数学理科第12题)研究问题:“已知关于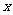 的不等式
的不等式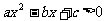 的解集为
的解集为 ,解关于
,解关于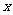 的不等式
的不等式
 ”,有如下解法:
”,有如下解法:
 解:由
解:由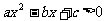

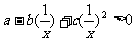 ,令
,令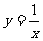 ,则
,则 ,
,
所以不等式 的解集为
的解集为 .
.
参考上述解法,已知关于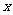 的不等式
的不等式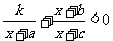 的解集为
的解集为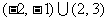 ,则
,则
关于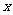 的不等式
的不等式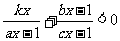 的解集为 .
的解集为 .
答案: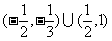
14. (浦东新区2008学年度第一学期期末质量抽测卷数学理科第10题)关于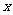 的方程
的方程 在区间
在区间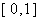 上有解,则实数
上有解,则实数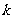
的取值范围是
.答案: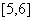
1 (2008学年度第一学期上海市普陀区高三年级质量调研第10题) 已知函数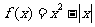 ,若
,若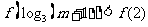 ,则实数
,则实数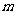 的取值范围是 .答案:
的取值范围是 .答案: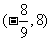
2 (闸北区09届高三数学(理)第5题) 设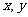 是满足
是满足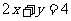 的正数,则
的正数,则 的最大值是
.答案:
的最大值是
.答案:
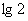 ;
;
3 (闸北区09届高三数学(理)第10题)设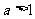 ,若仅有一个常数c使得对于任意的
,若仅有一个常数c使得对于任意的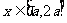 ,都有
,都有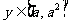 满足方程
满足方程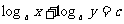 ,这时,
,这时,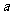 的取值的集合为
.
的取值的集合为
.
答案:
4(上海市静安区2008学年高三年级第一次质量调研第12题)(文)已知关于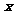 的不等式
的不等式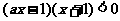 的解集是
的解集是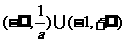 ,则实数
,则实数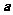 的取值范围是___________.
的取值范围是___________.
答案:
5 (上海市静安区2008学年高三年级第一次质量调研第12题)(理)已知关于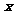 的不等式组
的不等式组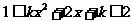 有唯一实数解,则实数
有唯一实数解,则实数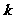 的取值集合是_________.答案:
的取值集合是_________.答案:
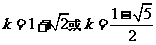
6 (闵行区2008学年第一学期高三质量监控理卷第3题)不等式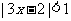 的解是
. 答案:
的解是
. 答案: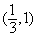
7 (静安区部分中学08-09学年度第一学期期中数学卷第11题)设函数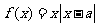 ,若对于任意
,若对于任意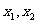
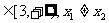 ,不等式
,不等式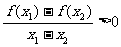 恒成立,则实数
恒成立,则实数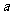 的取值范围是 .答案:
的取值范围是 .答案: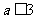
8 (闵行区2008学年第一学期高三质量监控理卷第11题)已知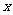 是
是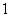 、
、 、
、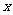 、
、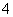 、
、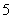 这五个数据的中位数,又知
这五个数据的中位数,又知 、
、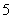 、
、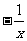 、
、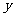 这四个数据的平均数为
这四个数据的平均数为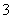 ,则
,则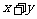 最小值为
. 答案:
最小值为
. 答案:
9 (闵行区2008学年第一学期高三质量监控理卷第12题)若关于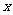 的不等式(组)
的不等式(组)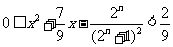 对任意
对任意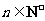 恒成立,则所
恒成立,则所
有这样的解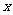 的集合是
. 答案:
的集合是
. 答案: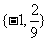
10 (闵行区2008学年第一学期高三质量监控数学文卷第12题)若关于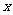 的不等式
的不等式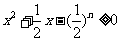 对任意
对任意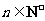 在
在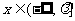 恒成立,则实常数
恒成立,则实常数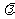 的取值范围是
. 答案:
的取值范围是
. 答案:
11 (南汇区2008学年度第一学期期末理科第6题)若由命题A: “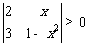 ”能推出命题B: “
”能推出命题B: “ ”,则
”,则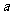 的取值范围是________.答案:
的取值范围是________.答案: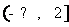
12 (南汇区2008学年度第一学期期末理科第13题)若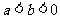 ,则下列结论中不恒成立的是( )
,则下列结论中不恒成立的是( )
A.  B.
B.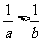 C.
C. 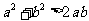 D.
D.
答案:D
13. (浦东新区2008学年度第一学期期末质量抽测卷数学理科第8题)无穷等比数列 各项和
各项和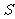 的值为2,公比
的值为2,公比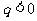 ,则首项
,则首项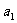 的取值范围是 .答案:
的取值范围是 .答案:
5.(上海市长宁区2008学年高三年级第一次质量调研5)若指数函数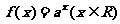 的部分对应值如右表:
的部分对应值如右表:
则不等式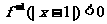 的解集为_____________.
的解集为_____________.
答案: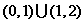
1(嘉定区2008-2009第一次质量调研第16题)已知关于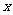 的不等式
的不等式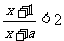 的解集为
的解集为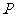 ,若
,若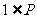 ,则实数
,则实数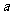 的取值范围为…( )
的取值范围为…( )
A.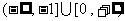 B.
B.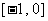 C.
C.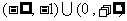 D.
D.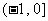
答案:B
2(2008学年度第一学期上海市普陀区高三年级质量调研第15题) 若不等式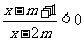 成立的一个充分非必要条件是
成立的一个充分非必要条件是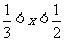 ,则
,则
实数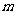 的取值范围是
( )
的取值范围是
( )
A.  ; B.
; B.  ; C.
; C.  ; D. 以上结论都不对.
; D. 以上结论都不对.
答案:B
3 (上海市静安区2008学年高三年级第一次质量调研第16题) 已知关于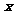 的不等式
的不等式 的解集为非空集合,则实数
的解集为非空集合,则实数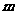 的取值范围是( )
的取值范围是( )
A. 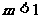 B.
B.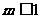 C.
C.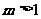 D.
D.
答案:C
4 (闵行区2008学年第一学期高三质量监控理卷第14题)如图为函数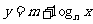 的图像,其中
的图像,其中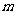 、
、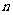 为常数,则下列结论正确的是
为常数,则下列结论正确的是
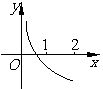 [答]( )
[答]( )
(A) 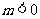 ,
,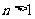 . (B)
. (B) 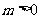 ,
,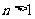 .
.
(C) 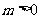 ,
,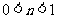 .
(D)
.
(D) 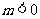 ,
,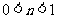 .
.
5 (南汇区2008学年度第一学期期末考试文科第13题)若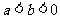 ,则下列结论中不恒成立的是( )
,则下列结论中不恒成立的是( )
A.  B.
B.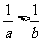 C.
C. 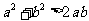 D.
D.
答案:D
4.(上海市八校2008学年第一学期高三数学考试试卷11)若不等式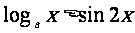
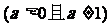 ,对于任意
,对于任意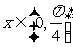 都成立,则实数
都成立,则实数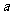 的取值范围
的取值范围
答案: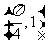
|
x |
-2 |
0 |
2 |
|
f(x) |
0.694 |
1 |
1.44 |
3. (上海市黄浦区2008学年高三年级第一次质量调研12)若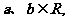 且
且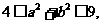 则
则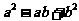 的最大值与最小值之和是_____________.
的最大值与最小值之和是_____________.
答案: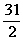
1. (上海虹口区08学年高三数学第一学期期末试卷1)若不等式: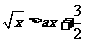 的解集是非空集合
的解集是非空集合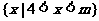 ,则
,则 ___________.
___________.
答案: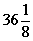
|
 的解是
。
的解是
。
答案: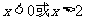
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com