
2. 宾语从句中
wish , would rather 后, 但would rather后所跟句子跟现在、将来相反用过去时,跟过去时间相反使用过去完成时。注意:不跟过去将来时。
I would rather you came tomorrow instead of today.我宁愿你明天而不是今天来。
1.在条件句中的运用
|
|
条件从句 |
主句 |
|
与现在事实相反 |
过去式(be一般用were) |
would
/ could/ might + v. |
|
与过去事实相反 |
had
+ 过去分词 |
would
/ could/ might+ have +过去分词 |
|
与将来事实相反 |
1) 过去式 2) should + v. 3) were to + v. |
would
/ could/ might + v. (第一人称可用should,以上同) |
1) “混合虚拟条件句”或“错综时间条件句”
主句和从句时间上不一致,从句可以和过去时间相反,主句可以与现在事实相反。
If you had taken my advice just now, you would be better now.
2) if 省略句。在条件句中,可省略if, 把were, had, should提到句首,变为倒装句式。
Were I you, I would seize the chance to go abroad.
3) 含蓄条件句
A) with, without, but for 等介词短语代替条件句
But for the rain, the crops would have died. (= If it hadn’t been for the rain)
B) 其他手段
I was ill that day. Otherwise, I would have taken part in the sports meeting.(副词)
He telephoned to inform me of your birthday, or I would have known nothing about it.(连词)
I might have given you more help, but I was too busy. (连词)
Given more time, we could have done it better. (分词短语)
It would be a mistake not to help him.(动词不定式)
2.主语从句中
1) It is necessary / important / strange / natural / a pity / a shame / no wonder … that….
eg. It is strange that he should have acted towards his parents like that.
二:形式为在原本的时态上退一步,即“+过去”
[要点点拨]
一:形式为(should) +v.
1.宾语从句中。一个坚持(insist),两个命令(order, command), 三条建议(advise, suggest, propose),四项要求(demand, require, request, ask).还有prefer ,advise等词。
注意:1)suggest和insist有例外
The smile on his face suggested that he was satisfied with our work.(“暗示”“表明”)
The man insisted that he had never stolen the money.
2) 这类动词的名词形式后的表语从句和同位语从句中也要用(should ) + v.形式。另外,还有plan, idea等词。
4.解:(1)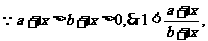
又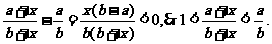
(2)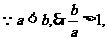 应用第(1)小题结论,得
应用第(1)小题结论,得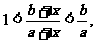 取倒数,得
取倒数,得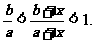
(3)由正弦定理,原题⇔△ABC中,求证: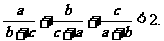
证明:由(2)的结论得,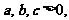 且
且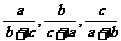 均小于1,
均小于1,
 ,
,

(4)如得出:四边形ABCD中,求证: 且证明正确给3分;
且证明正确给3分;
如得出:凸n边形A1A2A3┅An中,边长依次为 求证:
求证:
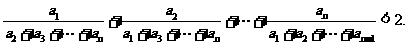 且证明正确给4分.
且证明正确给4分.
如能应用到其它内容有创意则给高分.
如得出: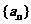 为各项为正数的等差数列,
为各项为正数的等差数列,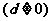 ,求证:
,求证:
 。
。
4. (上海虹口区08学年高三数学第一学期期末试卷21)(本题满分18分)第1小题4分,第2小题4分,第3小题5分,第4小题5分.
(1)已知: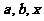 均是正数,且
均是正数,且 ,求证:
,求证: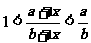 ;
;
(2)当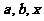 均是正数,且
均是正数,且 ,对真分数
,对真分数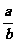 ,给出类似上小题的结论,并予以证明;
,给出类似上小题的结论,并予以证明;
(3)证明:△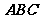 中,
中, (可直接应用第(1)、(2)小题结论)
(可直接应用第(1)、(2)小题结论)
(4)自己设计一道可直接应用第(1)、(2)小题结论的不等式证明题,并写出证明过程.
3.解:(1) ,即
,即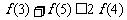
但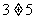 ,所以
,所以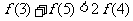
(若答案写成 ,扣一分)
(4分)
,扣一分)
(4分)
(2)① 对于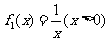 ,取
,取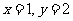 ,则
,则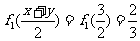
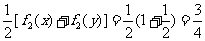
所以 ,
, .
(6分)
.
(6分)
②对于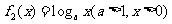 任取
任取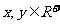 ,则
,则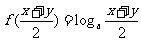
∵  ,而函数
,而函数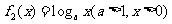 是增函数
是增函数
∴  ,即
,即
则 ,即
,即 .
(10分)
.
(10分)
(3)设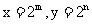 ,则
,则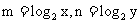 ,且m+n=1.
,且m+n=1.
由(2)知:函数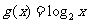 满足
满足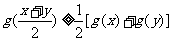 ,
,
得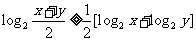 ,即
,即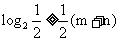 ,则
,则 (14分)
(14分)
当且仅当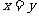 ,即
,即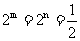 ,即m=n=-1时,m+n有最大值为-2. (16分)
,即m=n=-1时,m+n有最大值为-2. (16分)
3.(上海市奉贤区2008年高三数学联考19)(本题满分16分.第一小题4分,第2小题6分,第3小题6分.)
我们将具有下列性质的所有函数组成集合M:函数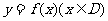 ,对任意
,对任意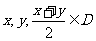 均满足
均满足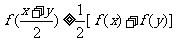 ,当且仅当
,当且仅当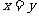 时等号成立.
时等号成立.
若定义在(0,+∞)上的函数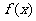 ∈M,试比较
∈M,试比较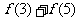 与
与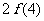 大小.
大小.
给定两个函数: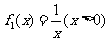 ,
,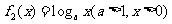 .
.
证明: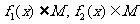 .
.
试利用(2)的结论解决下列问题:若实数m、n满足 ,求m+n的最大值.
,求m+n的最大值.
2.解: 当 时,P=
时,P=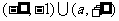
当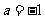 时,P=
时,P=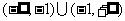
当 时,P=
时,P=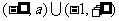 ----------6分
----------6分
Q:

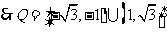 ------9分
------9分
 ---------10分
---------10分
若Q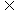 P
P 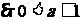 ---------12分
---------12分
2.(上海市八校2008学年第一学期高三数学考试试卷17)(本小题满分12分)
关于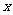 的不等式
的不等式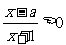 的解集为P,不等式
的解集为P,不等式 的解集为Q. 若Q
的解集为Q. 若Q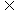 P, 求正数
P, 求正数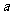 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com