

2、(2009揭阳)已知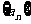 是等差数列,
是等差数列,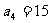 ,
,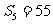 ,则过点
,则过点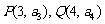 的直线的斜率( )A
的直线的斜率( )A
A.4 B.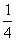 C.-4 D.-14
C.-4 D.-14
1、(2009潮州)等比数列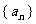 的首项与公比分别是复数
的首项与公比分别是复数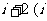 是虚数单位
是虚数单位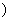 的实部与虚部,则数列
的实部与虚部,则数列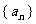 的前
的前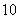 项的和为( )A
项的和为( )A
A  B
B 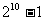 C
C
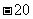 D
D 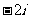
12、解:(Ⅰ)解法一:易知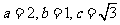 ,所以
,所以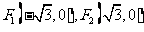 …………1分,设
…………1分,设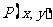 ,则
,则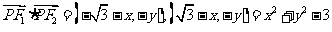 …………3分
…………3分
因为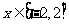 ,故当
,故当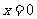 ,即点
,即点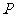 为椭圆短轴端点时,
为椭圆短轴端点时,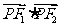 有最小值
有最小值 …5分
…5分
当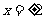 ,即点
,即点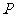 为椭圆长轴端点时,
为椭圆长轴端点时,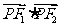 有最大值
有最大值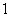 …………7分
…………7分
解法二:易知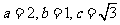 ,所以
,所以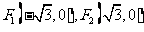 …………1分,
…………1分,
设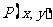 ,则
,则

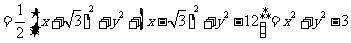 …………3分(以下同解法一)
…………3分(以下同解法一)
(Ⅱ)显然直线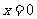 不满足题设条件…………8分,
不满足题设条件…………8分,
可设直线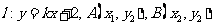 ,
,
联立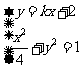 ,消去
,消去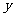 ,整理得:
,整理得: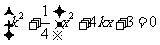 …………9分
…………9分
由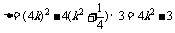 >0得:
>0得: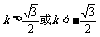 …………12分
…………12分
11、解:(1)设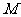 为动圆圆心,由题意知:
为动圆圆心,由题意知: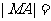
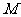 到定直线
到定直线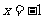 的距离,
的距离,
由抛物线的定义知,点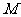 的轨迹为抛物线,其中
的轨迹为抛物线,其中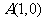 为焦点,
为焦点,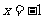 为准线,
为准线,
∴ 动圆的圆心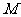 的轨迹
的轨迹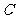 的方程为:
的方程为: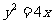 ………………………5分
………………………5分
(2)由题意可设直线 的方程为
的方程为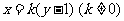 ,
,
由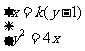 得
得 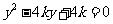
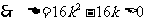

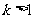 或
或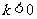 ………………………7分
………………………7分
且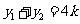 ,
,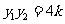 …………………………………9分
…………………………………9分
由

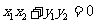 …………………………………………11分
…………………………………………11分

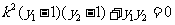

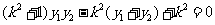

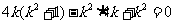

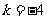 或
或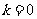 (舍去) …………………13分
(舍去) …………………13分
又 ,所以直线
,所以直线 存在,其方程为:
存在,其方程为: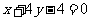 ………………14分
………………14分
10、解: (Ⅰ)由题设知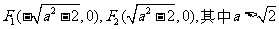
由于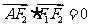 ,则有
,则有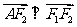 ,所以点
,所以点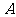 的坐标为
的坐标为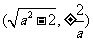 ……..2分
……..2分
故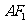 所在直线方程为
所在直线方程为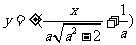 …………3分
…………3分
所以坐标原点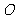 到直线
到直线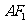 的距离为
的距离为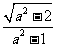
又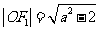 ,所以
,所以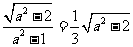 解得:
解得: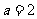 ………….5分
………….5分
所求椭圆的方程为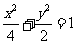 …………7分
…………7分
(Ⅱ)由题意可知直线 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为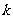
直线 的方程为
的方程为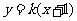 ,则有
,则有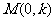 …………9分
…………9分
设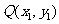 ,由于
,由于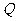 、
、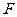 、
、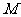 三点共线,且
三点共线,且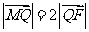
根据题意得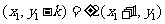 解得
解得 或
或 …………12分
…………12分
又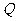 在椭圆
在椭圆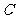 上,故
上,故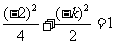 或
或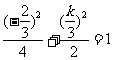 解得
解得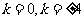
综上,直线 的斜率为
的斜率为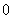 或
或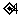 .…………14分
.…………14分
9、解:(I)设动点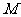 的坐标为
的坐标为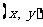 ,由于动点
,由于动点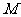 到点
到点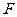 的距离与到直线
的距离与到直线 的距离之比为
的距离之比为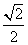 ,故
,故 ,
2分
,
2分
化简得: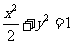 ,这就是动点
,这就是动点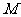 的轨迹方程.
6分
的轨迹方程.
6分
(II)设直线AB的方程为
代入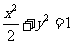 ,整理得
,整理得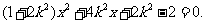
∵直线AB过椭圆的左焦点F,∴方程有两个不等实根, 8分
 记
记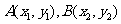 ,
,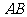 中点
中点 , 则
, 则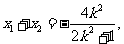
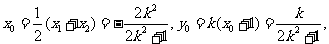
∵线段AB的中点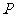 在直线
在直线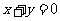 上,
上,
∴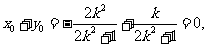 ∴
∴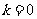 ,或
,或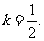 10分
10分
当直线AB与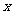 轴垂直时,线段AB的中点F不在直线
轴垂直时,线段AB的中点F不在直线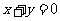 上,
上,
∴直线AB的方程是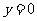 或
或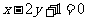 .
14分
.
14分
8、解:(1)过C: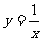 上一点
上一点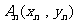 作斜率为
作斜率为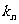 的直线交C于另一点
的直线交C于另一点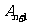 ,
,
则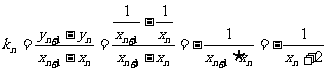 , ----------------------------3分
, ----------------------------3分
于是有: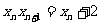 即:
即: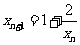 ----------------------------4分
----------------------------4分
(2)记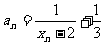 ,则
,则
 , ----------------6分
, ----------------6分
因为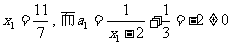 ,
,
因此数列{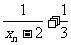 }是等比数列。
----------------------------8分
}是等比数列。
----------------------------8分
(3)由(2)可知: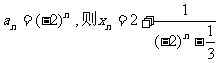 ,
,
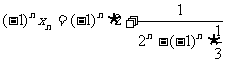 。
----------------------------9分
。
----------------------------9分
当n为偶数时有: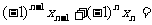
= , -----------------11分
, -----------------11分
于是
①在n为偶数时有:
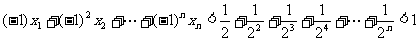 。 -----------------12分
。 -----------------12分
②在n为奇数时,前n-1项为偶数项,于是有:
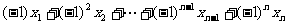
 。 -----------------13分
。 -----------------13分
综合①②可知原不等式得证。 ----------------------------14分
7、解:(1)∵点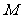 是线段
是线段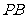 的中点 ∴
的中点 ∴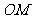 是△
是△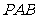 的中位线
的中位线
又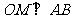 ∴
∴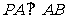 ----------------------------2分
----------------------------2分
∴ ---------------------------7分
---------------------------7分
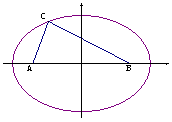 ∴椭圆的标准方程为
∴椭圆的标准方程为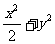 =1
----------8分
=1
----------8分
(2)∵点C在椭圆上,A、B是椭圆的两个焦点
∴AC+BC=2a=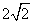 ,AB=2c=2
-------------------------10分
,AB=2c=2
-------------------------10分
在△ABC中,由正弦定理,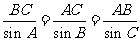 -----------12分
-----------12分
∴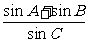 =
=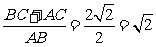 ------------------14分
------------------14分
6、解:(Ⅰ)由题意得: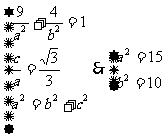 所以椭圆的方程为
所以椭圆的方程为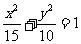
(Ⅱ)由题可知当直线PA过圆M的圆心(8,6)时,弦PQ最大因为直线PA的斜率一定存在, 设直线PA的方程为:y-6=k(x-8)
又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为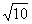
即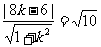 可得
可得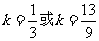
所以直线PA的方程为: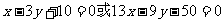
(Ⅲ)设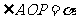 则
则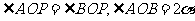
则
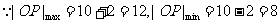
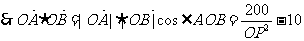
5、解:(1)设C、D点的坐标分别为C(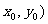 ,D
,D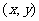 ,则
,则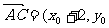 ),
),
 , 则
, 则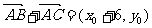 ,故
,故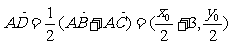
又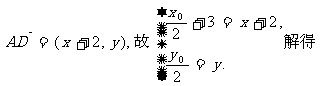
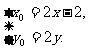
代入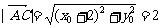 中, 整理得
中, 整理得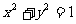 ,即为所求点D的轨迹方程.
,即为所求点D的轨迹方程.
(2)易知直线 与
与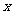 轴不垂直,设直线
轴不垂直,设直线 的方程为
的方程为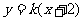 ①.
①.
又设椭圆方程为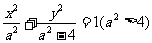 ②.
②.
因为直线 :kx-y+2k=0与圆
:kx-y+2k=0与圆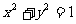 相切.故
相切.故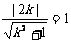 ,解得
,解得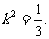
将①代入②整理得,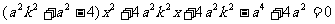 ③
③
将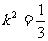 代入上式,整理得
代入上式,整理得 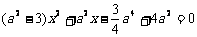 ,
,
设M(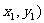 ,N(
,N(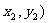 ,则
,则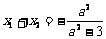 ,
,
由题意有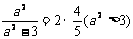 ,求得
,求得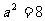 .经检验,此时③的判别式
.经检验,此时③的判别式
故所求的椭圆方程为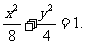
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com