
1、(1) 解法一:由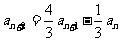 ,得
,得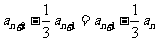 ,
,
∴数列 是常数列,
是常数列,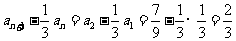 ,
,
即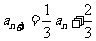 ,得
,得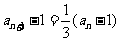 .
.
∴数列 是首项为
是首项为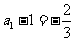 ,公比为
,公比为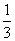 的等比数列,
的等比数列,
∴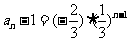 ,故数列
,故数列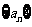 的通项公式为
的通项公式为 . …………5分
. …………5分
解法二:由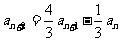 ,得
,得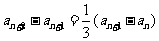 ,
,
∴数列 是首项为
是首项为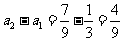 ,公比为
,公比为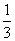 的等比数列,
的等比数列,
∴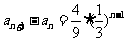 .
.
∴
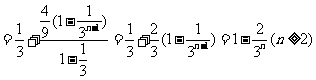 (*)
(*)
当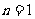 时,
时,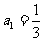 也适合(*),故数列
也适合(*),故数列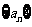 的通项公式为
的通项公式为 . ………5分
. ………5分
解法三:由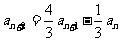 ,得
,得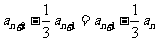 ,
,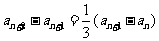 .
.
∴ 是常数列,
是常数列, 是首项为
是首项为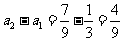 ,公比为
,公比为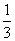 的等比数列.
的等比数列.
∴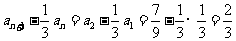 ,且
,且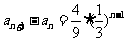 .
.
由上式联立消去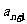 ,解得:
,解得: 为数列
为数列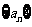 的通项公式. …………5分
的通项公式. …………5分
解法四:由已知,有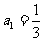 ,
,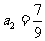 ,
,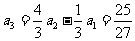 ,从而猜想:
,从而猜想: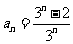 .
.
下用第二数学归纳法证明:
① 当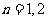 时,结论显然成立.
时,结论显然成立.
② 假设当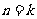 和
和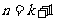 时结论成立,即
时结论成立,即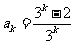 ,
,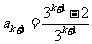 ,
,
则当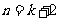 时,
时,
 ,即当
,即当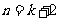 时结论也成立.
时结论也成立.
综上,数列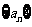 的通项公式为
的通项公式为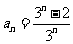 .
…………5分
.
…………5分
(2) 解: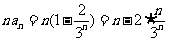 .
.
设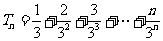 , ①
, ① 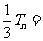
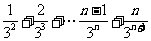 . ②
. ②
①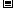 ②得:
②得: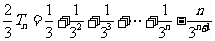
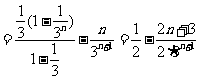 ,
,
∴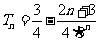 .
.
故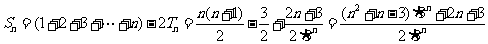 . …9分
. …9分
(3) 证: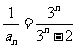 .
.
∵不等式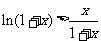 对
对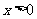 成立,令
成立,令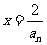 ,得
,得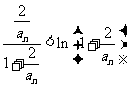 ,即
,即
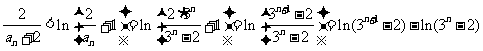 . 于是
. 于是
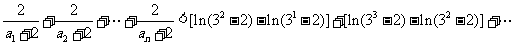
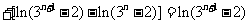 .
.
∴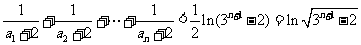 .
…………14分
.
…………14分
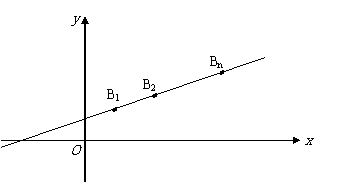
11、(2009番禺)已知点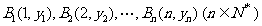 在直线
在直线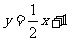 上,点
上,点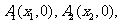
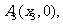 ……,
……,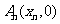 顺次为
顺次为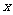 轴上的点,其中
轴上的点,其中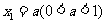 ,对于任意
,对于任意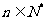 ,点
,点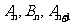 构成以
构成以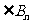 为顶角的等腰三角形, 设
为顶角的等腰三角形, 设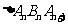 的面积为
的面积为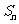 .
.
(1)
证明:数列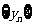 是等差数列;
是等差数列;
(2)
求 ;(用
;(用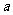 和
和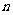 的代数式表示)
的代数式表示)
(3)
 设数列
设数列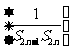 前
前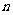 项和为
项和为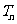 ,判断
,判断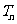 与
与 (
(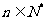 )的大小,并证明你的结论;
)的大小,并证明你的结论;
祥细答案:
10、(2009广东六校一)已知数列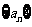 的首项
的首项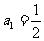 ,前
,前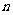 项和
项和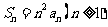 .
.
(Ⅰ)求数列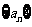 的通项公式;
的通项公式;
(Ⅱ)设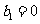 ,
,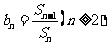 ,
,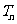 为数列
为数列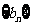 的前
的前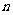 项和,求证:
项和,求证: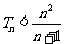 .
.
9、(2009潮南)在数列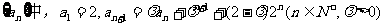
(1) 求数列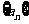 的通项公式;
的通项公式;
(2) 求数列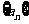 的前n项和
的前n项和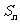 ;
;
(3) 证明存在
8、(2009广东中山期末)已知数列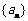 是首项为
是首项为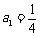 ,公比
,公比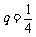 的等比数列,设
的等比数列,设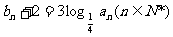 ,数列
,数列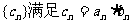 .
.
(1)求数列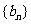 的通项公式;(2)求数列
的通项公式;(2)求数列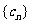 的前n项和Sn.
的前n项和Sn.
7、(2009广东湛江)已知数列 是等比数列,且
是等比数列,且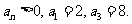
(1)求数列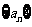 的通项公式; (2)求证:
的通项公式; (2)求证: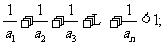
(3)设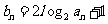 ,求数列
,求数列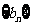 的前100项和.
的前100项和.
6、(2009广州海珠)数列
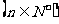 是递增的等比数列,且
是递增的等比数列,且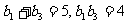 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若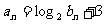 ,求证数列
,求证数列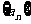 是等差数列;
是等差数列;
(Ⅲ)若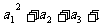 ……
…… ,求
,求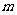 的最大值.
的最大值.
5、(2009广东揭阳)已知数列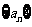 满足
满足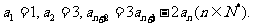
(I)证明:数列 是等比数列;(II)求数列
是等比数列;(II)求数列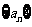 的通项公式;
的通项公式;
(II)若数列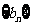 满足
满足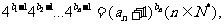 证明
证明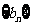 是等差数列。
是等差数列。
4、(09北江中学期末)若数列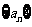 的前
的前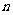 项和为
项和为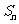 ,
,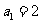 且
且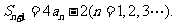
(I)求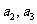 ;
;
(II)求证:数列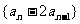 是常数列;
是常数列;
(III)求证: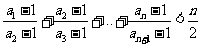 .
.
3、(09广东四校文期末)已知函数 f (x) = a x 2 + bx -的图象关于直线x=-对称, 且过定点(1,0);对于正数列{an},若其前n项和Sn满足Sn = f (an) (n Î N*)
(Ⅰ)求a , b的值;
(Ⅱ)求数列{an} 的通项公式;
(Ⅲ)设bn = (n Î N*),若数列{bn} 的前n项和为Tn,试比较Tn与5的大小,并证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com