
8、解:(Ⅰ)设甲、乙两人考试合格的事件分别为A、B,则
P(A)=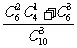 =
=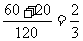 ,P(B)=
,P(B)=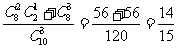 . ………3分
. ………3分
因为事件A、B相互独立,
∴甲、乙两人考试均合格的概率为  ……………………5分
……………………5分
答:甲、乙两人考试均合格的概率为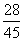 . …………………………6分
. …………………………6分
(Ⅱ)依题意, =0,1,2,3,………………7分
=0,1,2,3,………………7分
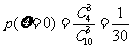 ,
, 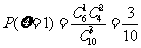 ,
,
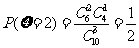 ,
, 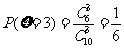 ……………………………9分
……………………………9分
甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
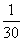 |
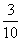 |
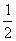 |
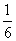 |
甲答对试题数ξ的数学期望

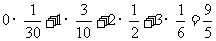 .
……………………12分
.
……………………12分
7、解(I)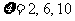 ……………………………………………………2分
……………………………………………………2分
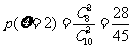 ,
,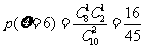 ,
,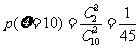 ……8分
……8分
 |
2 |
6 |
10 |
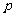 |
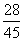 |
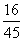 |
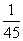 |
所以 的概率分布列为:
的概率分布列为:
………………………10分
(II)由(I)知,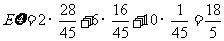 ………………………12分
………………………12分
所以抽奖人获利的数学期望为: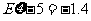 元。 ………………………14分
元。 ………………………14分
6、解:(1)从50名教师随机选出2名的方法数为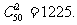
选出2人使用版本相同的方法数为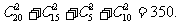
故2人使用版本相同的概率为:
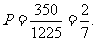 …………………………5分
…………………………5分
(2)∵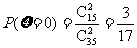 ,
, 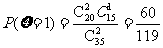
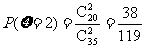
 |
0 |
1 |
2 |
|
P |
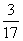 |
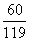 |
 |
∴ 的分布列为
的分布列为
………………10分
∴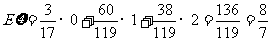 ……………………12分
……………………12分
5、解:(Ⅰ)设甲获第一、丙获第二、乙获第三为事件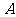 ,
,
则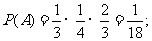 ············································································ 6分
············································································ 6分
(Ⅱ)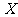 可能的取值为
可能的取值为
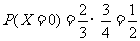 ,
,
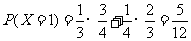 ,
,
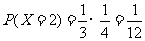 ,··········································································· 12分
,··········································································· 12分
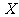 |
0 |
1 |
2 |
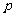 |
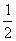 |
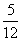 |
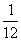 |
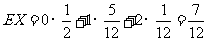 ······························································· 14分
······························································· 14分
4、解:(1)设掷两颗正方体骰子所得的点数记为(x,y),其中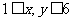 ,
,
则获一等奖只有(6,6)一种可能,其概率为: ; …………2分
; …………2分
获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,其概率为: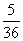 ;
;
…………5分
设事件A表示“同行的三位会员一人获一等奖、两人获二等奖”,则有:
P(A)= ;
…………6分
;
…………6分
|
ξ |
30-a |
-70 |
0 |
30 |
|
p |
 |
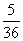 |
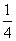 |
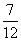 |
(2)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为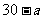 ,
,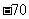 ,0,
,0,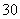 ,…7分
,…7分
其分布列为:
则:Eξ= ; …………11分
; …………11分
由Eξ=0得:a=310,即一等奖可设价值为310 元的奖品。 …………12分
3、解: 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且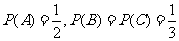 .------------------------------------------------------2分
.------------------------------------------------------2分
(1)至少有1人面试合格的概率是
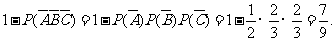 ----------------------4分
----------------------4分
(2)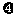 的可能取值为0,1,2,3.----------------------------------------------------------5分
的可能取值为0,1,2,3.----------------------------------------------------------5分
∵ 
=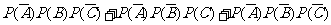
=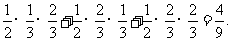 ---------------------------6分
---------------------------6分
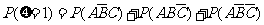
=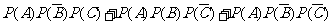
=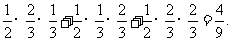 --------------------------------7分
--------------------------------7分
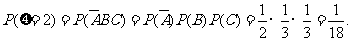 ---------------------8分
---------------------8分
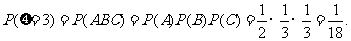 ----------------------9分
----------------------9分
∴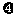 的分布列是
的分布列是
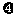 |
0 |
1 |
2 |
3 |
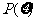 |
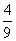 |
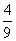 |
 |
 |
--------10分
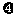 的期望
的期望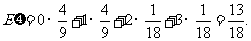 ----------------------------------------12分
----------------------------------------12分
2、解: 由题意可知,飞镖落在靶内各个区域的概率与它们的面积成正比,而与它们的质量和形状无关。
由圆的半径值可得到三个同心圆的半径之比为3:2:1,面积比为9:4:1
所以8环区域、9环区域、10环区域的面积比为5:3:1 ………3分
则掷得8环、9环、10环的概率分别设为5k,3k,k
根据离散型随机变量分布列的性质有0.1+5k+3k+k=1
解得k=0.1 ………6分
得到离散型随机变量x的分布列为
|
x |
0 |
8 |
9 |
10 |
|
P |
0.1 |
0.5 |
0.3 |
0.1 |
………9分
Ex=0×0.1+8×0.5+9×0.3+10×0.1=7.7 ………12分
1、解: (Ⅰ)从2种服装商品,2种家电商品,3种日用商品中,选出3种商品一共有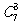 种选法,.选出的3种商品中没有日用商品的选法有
种选法,.选出的3种商品中没有日用商品的选法有 种, ……1分.
种, ……1分.
所以选出的3种商品中至少有一种日用商品的概率为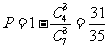 .……4分
.……4分
(Ⅱ)顾客在三次抽奖中所获得的奖金总额是一随机变量,设为X,其所有可能值为0, 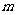 ,2
,2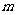 ,3
,3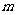 .……6分
.……6分
X=0时表示顾客在三次抽奖中都没有获奖,所以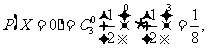 ……7分
……7分
同理可得 ……8分
……8分
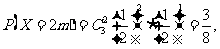 ……9分
……9分
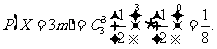 ……10分
……10分
于是顾客在三次抽奖中所获得的奖金总额的期望值是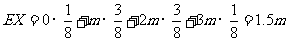 .……12分
.……12分
要使促销方案对商场有利,应使顾客获奖奖金总额的期望值不大于商场的提价数额,因此应有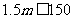 ,所以
,所以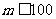 ,……13分.
,……13分.
故商场应将中奖奖金数额最高定为100元,才能使促销方案对商场有利. ……14分
8、(2009广东深圳)甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲、乙两人考试均合格的概率;
(Ⅱ)求甲答对试题数 的概率分布及数学期望.
的概率分布及数学期望.
祥细答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com