
20. (本小题满分14分)
已知向量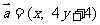 , 向量
, 向量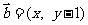 , 且
, 且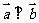 , 动点
, 动点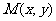 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B, 且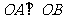 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
高级中学2010-2011学年第一学期高三第一次测试
19.(本小题满分14分)
如图,过抛物线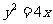 上一点P(
上一点P(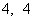 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(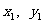 ),B(
),B(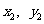 ).
).
直线PA与PB的斜率存在且互为相反数,(1)求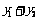 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.
18. (本小题满分14分)
已知动圆 经过点
经过点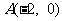 ,且与圆
,且与圆 内切.
内切.
(1)求动圆圆心 的轨迹
的轨迹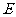 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点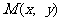 到定点B(1,0)的距离
到定点B(1,0)的距离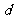 的最小值,并求
的最小值,并求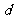 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.
17. (本小题满分14分)
(1)掷两颗骰子,其点数之和为4的概率是多少?
(2)甲、乙两人约定上午9点至12点在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,一小时之内如对方不来,则离去。如果他们二人在8点到12点之间的任何时刻到达约定地点的概率都是相等的,求他们见到面的概率。
16.(本小题满分12分)
已知圆经过点A(2,-3)和B(-2,-5).
(1)若圆心在直线x-2y-3=0上,求圆的方程. (2)若圆的面积最小,求圆的方程;
15. (本小题满分12分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
|
|
文艺节目 |
新闻节目 |
总计 |
|
20至40岁 |
42 |
16 |
58 |
|
大于40岁 |
18 |
24 |
42 |
|
总计 |
60 |
40 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名观众,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
14.设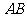 是椭圆
是椭圆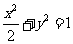 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,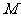 为
为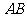 的中点,
的中点,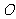 为坐标原点,则
为坐标原点,则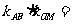 ****
****
13.圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为 ****
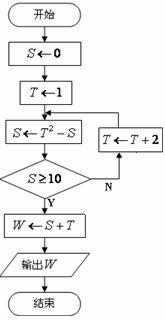
12.
 如下图所示,墙上挂有一边长为
如下图所示,墙上挂有一边长为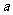 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为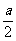 的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是 ****
的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是 ****
11. 右图是一个算法的流程图,最后输出的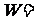 ****
****
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com