4. 已知一次函数y=(k-2)x+(k+2),若它的图象经过原点,则k=_____;若y随x的增大而增大,则k__________.

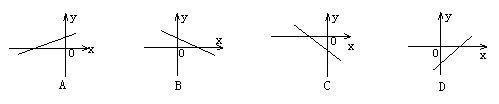*5.若一次函数y=kx-b满足kb<0,且函数值随x的减小而增大,则它的大致图象是图中的(　　 )

目标4　 会用待定系数法确定一次函数的解析式。

3.一次函数y=-2x+4的图象经过的象限是_______,它与x轴的交点坐标是_____,与y轴的交点坐标是_______.

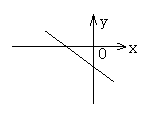
2. 一次函数y=mx+n的图象如图,则下面正确的是(　 )

　 A.m<0,n<0　　 B.m<0,n>0 　　C.m>0,n>0　　 D.m>0,n<0

1. 正比例函数y=kx,若y随x的增大而减小,则k______.

目标1　 知道什么是函数，并能判断某变化过程中两个变量之间的的关系是否函数关系

已知梯形上底的长为x，下底的长是10，高是6，梯形的面积y随上底x的变化而变化。

(1)梯形的面积y与上底的长x之间的关系是否是函数关系？为什么？　

(2)若y是x的函数，试写出y与x之间的函数关系式。

目标2 　知道什么是一次函数、正比例函数，并能判断一个函数是不是一次函数和正比例函数

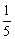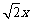1.函数:①y=-x x;②y=-1;③y=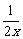;④y=x²+3x-1;⑤y=x+4;⑥y=3. 6x, 一次函数有___　　　　 __;正比例函数有____________(填序号).

*2.函数y=(k²-1)x+3是一次函数,则k的取值范围是(　 )A.k≠1　 B.k≠-1 　C.k≠±1　 D.k为任意实数．

*3．若一次函数y=(1+2k)x+2k-1是正比例函数,则k=_______.

目标3 　会运用一次函数图像及性质解决简单的问题

4、一次函数图像、性质及其解析式的确定：

3、判断一个函数是不是一次函数的条件：

(1)、　　　　 　的个数；(2)、自变量的　　　 和　　　　 ；(3)、分母中是否含有　　　　

2、一次函数的概念：若两个变量x,y间的函数关系式可以表示成　　　　 　　　　　　的形式，则称 　　

　 　是　 的一次函数， 　　为自变量，　　　 为因变量。特别地，　　　　 时，称　　　　　　　　 。

正比例函数是_____________的特殊形式,因此正比例函数都是_______,而一次函数不一定都是_________.

1、函数的概念：一般地，在某个变化过程中，有两个变量x和y,如果给定一个x值, 相应地就唯一确定了一个y值,那么就　　　 是_____ 的函数；

4、　 会用待定系数法确定一次函数的解析式。